Permutation groups consist of all the bijections from a set onto itself, equipped with the operation of composition, forming a fundamental structure in abstract algebra. These groups characterize symmetry and play a crucial role in fields such as combinatorics, geometry, and group theory. Explore this article to deepen your understanding of permutation groups and their applications in mathematics.
Table of Comparison
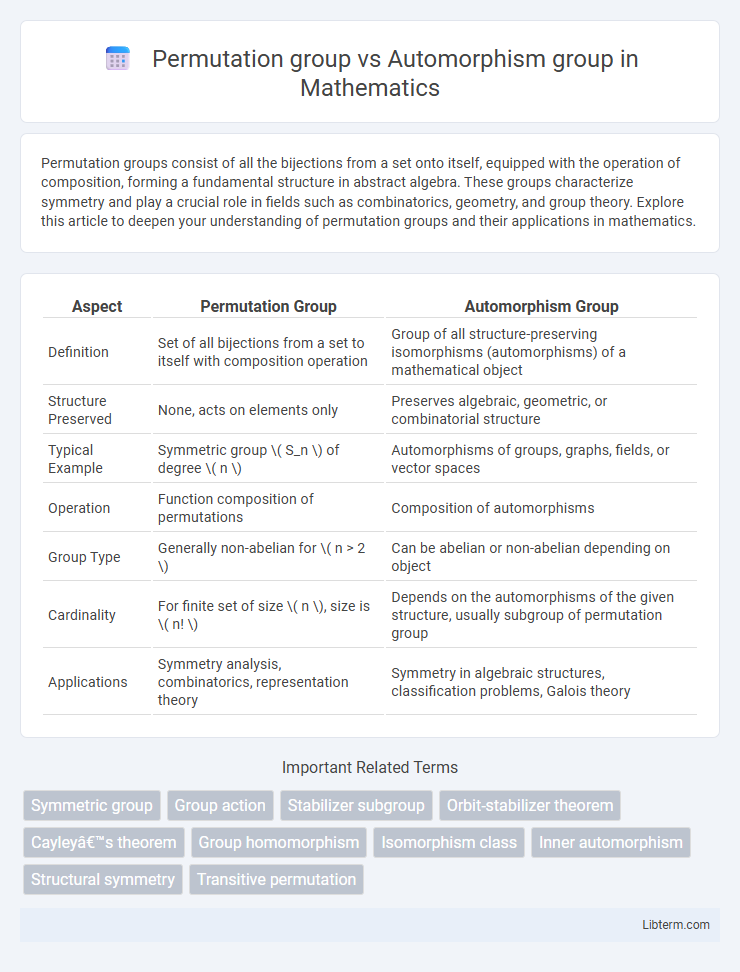
| Aspect | Permutation Group | Automorphism Group |
|---|---|---|
| Definition | Set of all bijections from a set to itself with composition operation | Group of all structure-preserving isomorphisms (automorphisms) of a mathematical object |
| Structure Preserved | None, acts on elements only | Preserves algebraic, geometric, or combinatorial structure |
| Typical Example | Symmetric group \( S_n \) of degree \( n \) | Automorphisms of groups, graphs, fields, or vector spaces |
| Operation | Function composition of permutations | Composition of automorphisms |
| Group Type | Generally non-abelian for \( n > 2 \) | Can be abelian or non-abelian depending on object |
| Cardinality | For finite set of size \( n \), size is \( n! \) | Depends on the automorphisms of the given structure, usually subgroup of permutation group |
| Applications | Symmetry analysis, combinatorics, representation theory | Symmetry in algebraic structures, classification problems, Galois theory |
Introduction to Permutation Groups
Permutation groups consist of all bijections from a set onto itself, where the group operation is composition of these permutations. They encapsulate the symmetric structure of sets by describing all possible rearrangements of elements, with the symmetric group \( S_n \) being the most fundamental example. Understanding permutation groups provides a foundation for exploring automorphism groups, which generalize these symmetries to more complex algebraic structures rather than just sets.
Understanding Automorphism Groups
Automorphism groups consist of all isomorphisms from a mathematical structure to itself, preserving its inherent properties, while permutation groups are sets of bijections on a set, focusing on rearranging elements without structural constraints. Understanding automorphism groups involves analyzing symmetries that maintain operations and relations within algebraic structures like graphs, groups, or fields. These groups reveal intrinsic structural symmetries, enabling classification and deeper insight into the object's fundamental characteristics beyond mere element permutations.
Fundamental Differences Between Permutation and Automorphism Groups
Permutation groups consist of all bijections from a set onto itself, operating strictly through rearrangements of elements, while automorphism groups include structure-preserving bijections of mathematical objects like graphs, groups, or fields. The fundamental difference lies in automorphism groups maintaining inherent algebraic or relational properties in addition to being permutations, making them subsets of permutation groups with additional constraints. Automorphisms preserve operational or relational consistency, whereas permutation groups do not necessarily respect internal structures but focus purely on element reordering.
Algebraic Structure Comparison
Permutation groups consist of all bijective functions from a set onto itself, with function composition as the group operation, emphasizing the action of rearranging elements. Automorphism groups form a subset of permutation groups preserving the underlying algebraic structure, such as group operations or relations, therefore respecting the object's intrinsic properties. The key difference lies in that permutation groups represent general symmetries as permutations, whereas automorphism groups capture structural symmetries maintaining algebraic invariants.
Key Examples of Permutation Groups
Permutation groups include the symmetric group \(S_n\), representing all permutations of \(n\) elements, and the alternating group \(A_n\), consisting of even permutations. Automorphism groups, such as the automorphism group of a graph or a group, describe structure-preserving symmetries maintaining algebraic or combinatorial properties. Key examples of permutation groups often illustrate fundamental concepts in group theory, with \(S_3\) exemplifying non-abelian behavior and the dihedral group \(D_n\) acting as the group of symmetries of an \(n\)-gon.
Key Examples of Automorphism Groups
Automorphism groups capture the symmetries of algebraic structures by consisting of isomorphisms from a structure to itself, preserving its operation, unlike permutation groups that act on sets without necessarily preserving structure. Key examples of automorphism groups include the automorphism group of a finite cyclic group, isomorphic to the multiplicative group of units modulo the group order, and the automorphism group of a graph, which consists of all vertex permutations preserving adjacency relations. Another fundamental example is the automorphism group of a field extension, central to Galois theory, where automorphisms fix the base field and reflect field symmetries that impact solvability of polynomial equations.
Applications in Mathematical Fields
Permutation groups play a crucial role in combinatorics and algebraic structures by describing symmetries of sets and facilitating the study of group actions on finite or infinite objects. Automorphism groups, essential in graph theory, topology, and model theory, capture the intrinsic symmetries of mathematical structures by preserving their relational properties and underlying operations. Both groups provide foundational tools for classifying objects up to isomorphism, analyzing symmetry properties in geometry, and solving equations through Galois theory in field extensions.
Role in Graph Theory and Symmetry
Permutation groups capture the symmetries of a graph by describing all bijections of its vertex set, fundamental in studying graph isomorphisms and symmetry properties. Automorphism groups form a subset of permutation groups consisting of vertex permutations that preserve edge connectivity, directly characterizing a graph's intrinsic symmetries. These groups enable the classification of graphs based on their symmetry structures, influencing algorithms for graph matching, coloring, and structural analysis.
Relationships and Interconnections
Permutation groups act on sets by rearranging elements, forming the foundation for understanding symmetries through bijections. Automorphism groups specialize this concept by focusing on structure-preserving bijections within algebraic objects, such as graphs or groups, illustrating intrinsic symmetries beyond mere element reordering. The interplay between these groups manifests as automorphism groups being subgroups of permutation groups that maintain essential relational properties, highlighting their interlinked roles in symmetry analysis.
Summary and Further Reading
Permutation groups consist of all bijections from a set onto itself, capturing the idea of rearrangements, while automorphism groups include all structure-preserving bijections of algebraic or combinatorial objects. Both groups highlight symmetries with permutation groups emphasizing element rearrangement and automorphism groups focusing on preserving relational or operational structure. For deeper understanding, consult texts such as "Abstract Algebra" by Dummit and Foote and "Groups and Symmetry" by Armstrong.
Permutation group Infographic
 libterm.com
libterm.com