Grothendieck duality provides a powerful framework in algebraic geometry for understanding the relationship between coherent sheaves and their duals on a proper morphism of schemes. This duality generalizes Serre duality and is instrumental in studying the cohomological behavior of morphisms, allowing you to compute derived functors and trace maps effectively. Explore the rest of the article to deepen your understanding of Grothendieck duality and its applications in modern algebraic geometry.
Table of Comparison
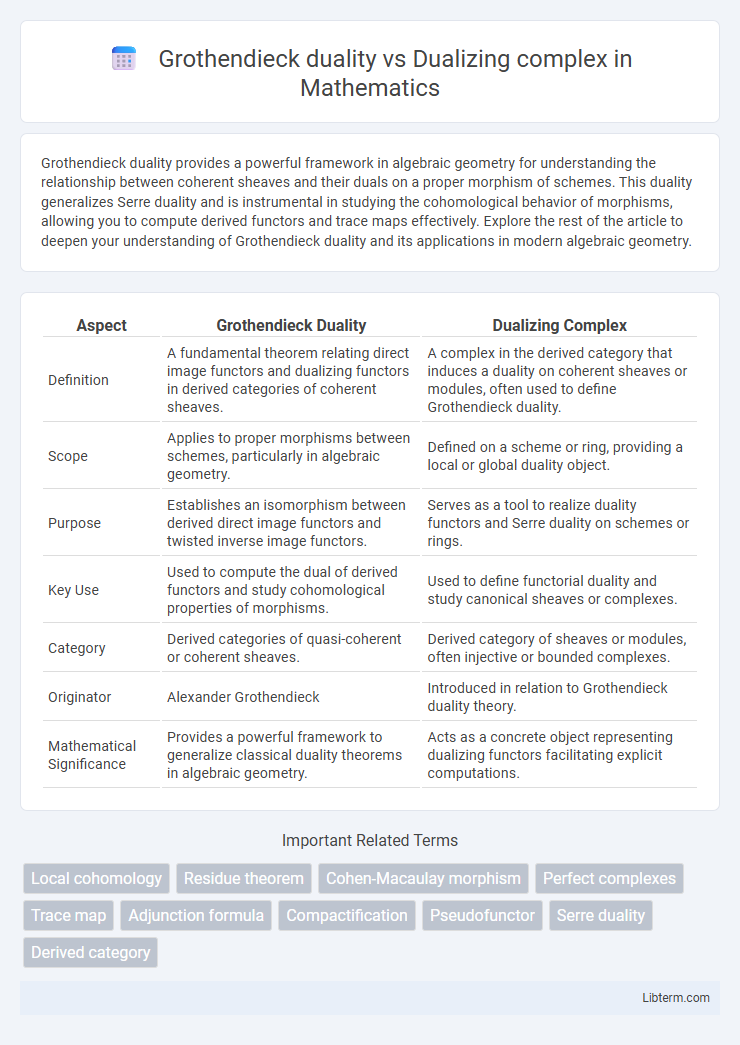
| Aspect | Grothendieck Duality | Dualizing Complex |
|---|---|---|
| Definition | A fundamental theorem relating direct image functors and dualizing functors in derived categories of coherent sheaves. | A complex in the derived category that induces a duality on coherent sheaves or modules, often used to define Grothendieck duality. |
| Scope | Applies to proper morphisms between schemes, particularly in algebraic geometry. | Defined on a scheme or ring, providing a local or global duality object. |
| Purpose | Establishes an isomorphism between derived direct image functors and twisted inverse image functors. | Serves as a tool to realize duality functors and Serre duality on schemes or rings. |
| Key Use | Used to compute the dual of derived functors and study cohomological properties of morphisms. | Used to define functorial duality and study canonical sheaves or complexes. |
| Category | Derived categories of quasi-coherent or coherent sheaves. | Derived category of sheaves or modules, often injective or bounded complexes. |
| Originator | Alexander Grothendieck | Introduced in relation to Grothendieck duality theory. |
| Mathematical Significance | Provides a powerful framework to generalize classical duality theorems in algebraic geometry. | Acts as a concrete object representing dualizing functors facilitating explicit computations. |
Introduction to Grothendieck Duality
Grothendieck duality provides a powerful framework for describing duality phenomena in the derived category of coherent sheaves on a scheme, generalizing classical Serre duality. It centers around the construction of a right adjoint to the derived pushforward functor, often realized through the dualizing complex, which encapsulates crucial geometric and homological information about the scheme. Understanding the dualizing complex is essential for applying Grothendieck duality, as it acts as a coherent object that induces the duality isomorphisms in a relative setting, especially in non-smooth or singular schemes.
What Is a Dualizing Complex?
A dualizing complex is a fundamental object in algebraic geometry providing a coherent sheaf or complex that serves as a "refined" dualizing object on a scheme, enabling the formulation of Grothendieck duality. It generalizes the notion of a dualizing sheaf by encoding the necessary homological data to establish a duality between derived categories of coherent sheaves. The existence of a dualizing complex on a scheme allows the construction of functors that describe how cohomological invariants transform under proper morphisms, thus underpinning Grothendieck duality theory.
Historical Background of Duality Theories
Grothendieck duality, developed in the 1960s by Alexander Grothendieck, revolutionized algebraic geometry by generalizing Serre duality to a relative setting of schemes, establishing a deep link between cohomology and dualizing complexes. The dualizing complex, originated from earlier ideas in homological algebra and complex geometry, serves as a fundamental tool to represent duality functors in derived categories, capturing local and global duality properties. This duality theory emerged as a unifying framework integrating sheaf theory, scheme theory, and homological methods, influencing subsequent advancements in algebraic and arithmetic geometry.
Key Definitions and Preliminaries
Grothendieck duality centers on a functorial isomorphism between the derived direct image and the derived Hom functor, establishing a duality theory for proper morphisms of schemes. A dualizing complex on a scheme X is an object in the derived category of coherent sheaves that induces a duality between the bounded derived category of coherent sheaves and its derived Hom. Key preliminaries include the notions of derived categories, adjoint functors, and coherent sheaf cohomology, which frame the construction and properties of both Grothendieck duality and dualizing complexes.
Grothendieck Duality: Statement and Scope
Grothendieck duality provides a fundamental framework relating the derived pushforward of a morphism of schemes to the derived pullback, establishing a duality between coherent sheaves in a relative setting. Its statement asserts the existence of a right adjoint to the derived pushforward functor, often constructed via a dualizing complex, and applies broadly to proper morphisms between noetherian schemes. The scope of Grothendieck duality extends to numerous areas such as coherent duality theory, local cohomology, and global duality phenomena in algebraic geometry, serving as a foundational tool for understanding dualizing complexes and their role in sheaf theory.
Dualizing Complexes: Construction and Examples
Dualizing complexes play a central role in Grothendieck duality by providing a framework for generalized duality on schemes beyond the classical setting of smooth varieties. They are constructed as bounded complexes of injective sheaves or modules that reflect the underlying geometric and homological properties of a scheme, enabling the definition of a dualizing functor compatible with the derived category structure. Key examples include the dualizing complex on a Gorenstein scheme, where it reduces to a shifted canonical bundle, and the complex associated to a Cohen-Macaulay scheme, illustrating how dualizing complexes generalize canonical sheaves and facilitate duality in singular or non-regular contexts.
Relationship Between Grothendieck Duality and Dualizing Complexes
Grothendieck duality provides a general framework for understanding adjunctions between derived functors in coherent sheaf theory, where dualizing complexes serve as fundamental objects realizing this duality explicitly. The dualizing complex on a scheme encodes the necessary data to establish the isomorphisms central to Grothendieck duality, making it a concrete tool to represent the dualizing functor. This relationship ensures that the abstract formalism of Grothendieck duality translates into computable and geometric terms via dualizing complexes.
Applications in Algebraic Geometry
Grothendieck duality provides a framework for understanding the relationship between direct and inverse image functors in derived categories, essential for formulating duality theorems on proper morphisms in algebraic geometry. The dualizing complex serves as a key object representing a coherent sheaf or complex that realizes this duality, enabling explicit calculations of cohomological invariants and residues. Applications include Serre duality generalizations, Riemann-Roch theorems, and the analysis of local cohomology, essential for studying singularities and the structure of algebraic varieties.
Major Differences and Comparative Analysis
Grothendieck duality is a fundamental theorem in algebraic geometry providing a duality between derived categories of coherent sheaves on a scheme, while the dualizing complex is a specific object that realizes this duality by serving as a kernel or reference complex. The major difference lies in scope: Grothendieck duality is the overarching duality framework, whereas the dualizing complex is a concrete construction used to implement this framework for a given morphism or scheme. Comparative analysis reveals that dualizing complexes vary with context--projective, Cohen-Macaulay, or Gorenstein schemes--whereas Grothendieck duality formulates a general categorical isomorphism, making the dualizing complex a tool within the broader duality theory.
Future Directions and Open Questions
Future directions in Grothendieck duality research focus on extending duality theorems to broader classes of schemes and enhancing computational tools for dualizing complexes. Open questions involve characterizing dualizing complexes in non-Noetherian contexts and understanding their behavior under derived categories and geometric morphisms. Advances may reveal deeper connections between homological algebra, derived geometry, and arithmetic geometry.
Grothendieck duality Infographic
 libterm.com
libterm.com