Understanding derivatives is essential for grasping changes in functions and analyzing rates of change in various fields such as physics, engineering, and finance. Derivatives provide insights into the behavior of functions by indicating slopes, maxima, and minima, which are critical for optimization problems. Explore the rest of the article to deepen your knowledge of derivatives and their applications.
Table of Comparison
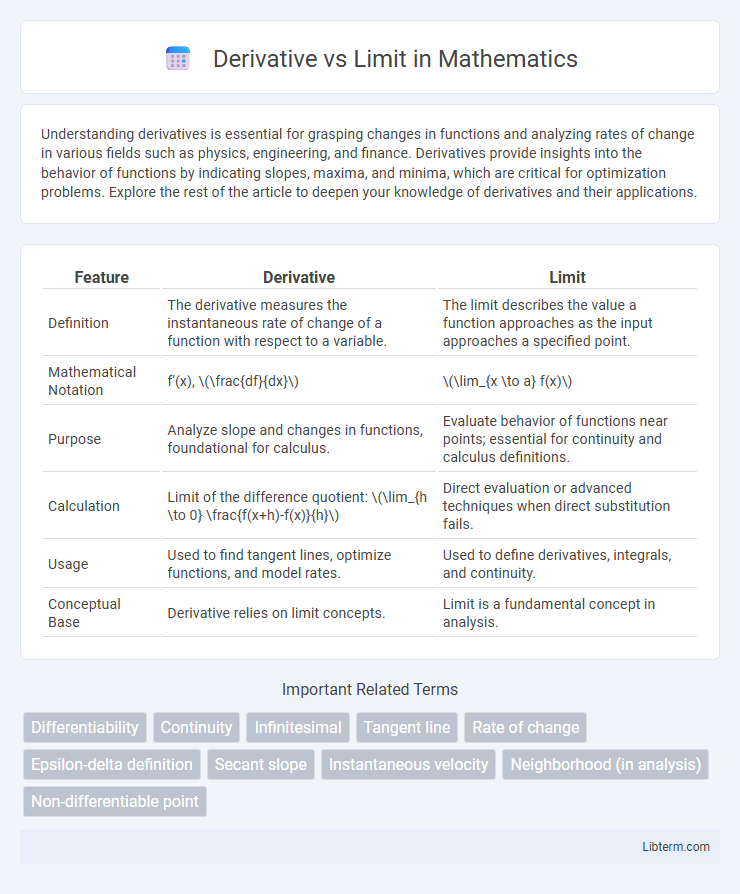
| Feature | Derivative | Limit |
|---|---|---|
| Definition | The derivative measures the instantaneous rate of change of a function with respect to a variable. | The limit describes the value a function approaches as the input approaches a specified point. |
| Mathematical Notation | f'(x), \(\frac{df}{dx}\) | \(\lim_{x \to a} f(x)\) |
| Purpose | Analyze slope and changes in functions, foundational for calculus. | Evaluate behavior of functions near points; essential for continuity and calculus definitions. |
| Calculation | Limit of the difference quotient: \(\lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\) | Direct evaluation or advanced techniques when direct substitution fails. |
| Usage | Used to find tangent lines, optimize functions, and model rates. | Used to define derivatives, integrals, and continuity. |
| Conceptual Base | Derivative relies on limit concepts. | Limit is a fundamental concept in analysis. |
Introduction to Derivatives and Limits
Derivatives measure the instantaneous rate of change of a function, defined as the limit of the average rate of change as the interval approaches zero. Limits establish the foundational concept required to rigorously define derivatives by describing the behavior of functions as inputs approach specific points. Understanding limits is essential for grasping how derivatives quantify slopes of tangent lines and rates of change in calculus.
Fundamental Definitions
A derivative represents the instantaneous rate of change of a function, defined as the limit of the average rate of change as the interval approaches zero. The formal definition uses the limit expression f'(x) = lim(h-0) [f(x+h) - f(x)] / h, capturing the slope of the tangent line at point x. Understanding limits is essential because they provide the foundational concept enabling the derivative to quantify how functions change at specific points.
Mathematical Relationship Between Derivative and Limit
The derivative of a function at a specific point is fundamentally defined as the limit of the average rate of change of the function as the interval approaches zero. Mathematically, the derivative f'(x) is expressed as the limit: f'(x) = lim(h-0) [f(x+h) - f(x)] / h, emphasizing the intrinsic relationship between the concepts of derivative and limit. This limit formulation captures the instantaneous rate of change, making the derivative a direct application of limit theory in calculus.
How Limits Are Used to Define Derivatives
Limits are fundamental in defining derivatives as they capture the instantaneous rate of change of a function. The derivative of a function at a point is the limit of the average rate of change as the interval approaches zero, expressed as lim(h-0) [f(x+h) - f(x)]/h. This limit process ensures the derivative accurately represents the slope of the tangent line to the function at a specific point.
Key Differences Between Derivatives and Limits
Derivatives represent the instantaneous rate of change of a function and are defined as the limit of the average rate of change as the interval approaches zero. Limits describe the value that a function approaches as the input approaches a specific point, serving as the foundational concept for defining derivatives. The key difference lies in that limits evaluate function behavior near a point, while derivatives quantify the exact slope or rate of change at that point.
Applications of Limits in Calculus
Limits form the foundational concept behind derivatives, enabling the precise calculation of instantaneous rates of change in functions. They are essential in determining continuity, evaluating function behavior near specific points, and solving problems in motion, growth, and optimization within calculus. Applications of limits extend to defining integrals, analyzing sequences, and understanding asymptotic behavior in mathematical modeling.
Real-World Applications of Derivatives
Derivatives play a crucial role in real-world applications by measuring the rate of change in various fields such as physics for velocity and acceleration, economics for marginal cost and revenue, and biology for growth rates. Unlike limits, which primarily provide the foundational concept of approaching values, derivatives directly quantify instantaneous changes, enabling precise modeling and optimization. This ability to capture dynamic behavior makes derivatives essential for predictive analytics, engineering design, and financial forecasting.
Common Misconceptions: Derivative vs Limit
A common misconception is that the derivative and the limit are interchangeable concepts, but the derivative specifically measures the instantaneous rate of change of a function, while a limit describes the value a function approaches as the input approaches a point. Another frequent error is assuming that every limit results in a derivative; however, limits can exist without defining a derivative, especially at points of discontinuity or sharp corners. Understanding that the derivative is a specific application of the limit concept applied to the difference quotient clarifies their distinct roles in calculus.
Visual Representation: Graphical Interpretation
The graphical interpretation of a derivative is the slope of the tangent line to a function's curve at a specific point, representing the instantaneous rate of change. In contrast, the limit visually corresponds to the value that the function's output approaches as the input nears a particular point. Understanding these visual cues helps distinguish how derivatives capture dynamic change while limits describe approaching behavior on a graph.
Summary: Choosing Between Derivative and Limit
Choosing between a derivative and a limit depends on the mathematical objective: derivatives measure the instantaneous rate of change of a function, while limits analyze the behavior of a function as it approaches a specific point. Derivatives require calculating the limit of the difference quotient, making limits foundational to understanding derivatives. For problems involving change and slope, derivatives are preferred, whereas limits are used for evaluating continuity and approaching values.
Derivative Infographic
 libterm.com
libterm.com