The Mellin transform is a powerful integral transform used in mathematical analysis to convert functions into a complex frequency domain, facilitating the solving of differential and integral equations. It plays a critical role in fields such as number theory, signal processing, and asymptotic analysis due to its ability to handle scale-invariant phenomena and multiplicative convolutions. Discover how understanding the Mellin transform can enhance your analytical toolkit by exploring the detailed applications and properties covered in the rest of this article.
Table of Comparison
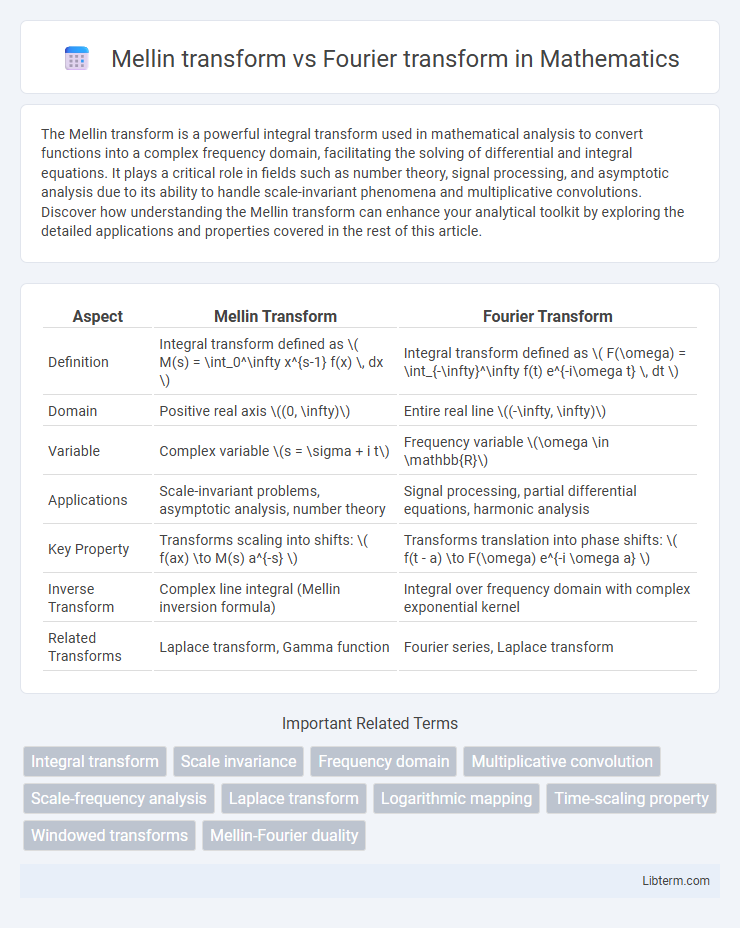
| Aspect | Mellin Transform | Fourier Transform |
|---|---|---|
| Definition | Integral transform defined as \( M(s) = \int_0^\infty x^{s-1} f(x) \, dx \) | Integral transform defined as \( F(\omega) = \int_{-\infty}^\infty f(t) e^{-i\omega t} \, dt \) |
| Domain | Positive real axis \((0, \infty)\) | Entire real line \((-\infty, \infty)\) |
| Variable | Complex variable \(s = \sigma + i t\) | Frequency variable \(\omega \in \mathbb{R}\) |
| Applications | Scale-invariant problems, asymptotic analysis, number theory | Signal processing, partial differential equations, harmonic analysis |
| Key Property | Transforms scaling into shifts: \( f(ax) \to M(s) a^{-s} \) | Transforms translation into phase shifts: \( f(t - a) \to F(\omega) e^{-i \omega a} \) |
| Inverse Transform | Complex line integral (Mellin inversion formula) | Integral over frequency domain with complex exponential kernel |
| Related Transforms | Laplace transform, Gamma function | Fourier series, Laplace transform |
Introduction to Mellin and Fourier Transforms
The Mellin transform is integral in analyzing functions characterized by scale invariance and multiplicative structures, mapping a function into the complex s-plane through integration against a power function x^(s-1). The Fourier transform decomposes a time or spatial domain signal into its frequency components by integrating against complex exponentials e^(-iox), facilitating analysis of periodicity and spectral content. Both transforms serve distinct but complementary roles in signal processing, with Mellin particularly effective for scale-invariant feature extraction and Fourier excelling in frequency and time-frequency analysis.
Mathematical Definitions and Formulations
The Mellin transform is defined as \( M\{f(t)\}(s) = \int_0^\infty t^{s-1} f(t) \, dt \), where \( s \) is a complex variable, mapping functions to the complex plane by scaling behaviors, useful in multiplicative scaling analysis. The Fourier transform is given by \( \mathcal{F}\{f(t)\}(\omega) = \int_{-\infty}^\infty f(t) e^{-i \omega t} \, dt \), mapping functions from the time domain to the frequency domain via oscillatory kernels, emphasizing frequency content. Both transforms involve integral kernels but differ fundamentally in their domains and applications: Mellin transform operates over positive real axis with power-law kernels, while Fourier transform operates over the entire real axis with exponential kernels.
Core Differences Between Mellin and Fourier Transforms
The Mellin transform analyzes functions by scaling and is particularly useful for problems involving multiplicative processes or scale-invariant phenomena, whereas the Fourier transform decomposes functions into sinusoidal frequencies, ideal for analyzing periodic or time-invariant signals. Mellin transforms convert convolution operations into products in a multiplicative domain, contrasting with Fourier transforms that do so in an additive frequency domain. The core mathematical distinction lies in Mellin's integration over positive real numbers with a kernel x^(s-1), compared to Fourier's integration over the entire real line with exponential kernels involving imaginary frequencies.
Domains of Application: Mellin vs Fourier
The Mellin transform excels in analyzing scale-invariant phenomena, making it ideal for applications in image processing, fractal analysis, and problems involving multiplicative scaling. The Fourier transform is predominantly used in signal processing, communications, and frequency analysis, handling time or spatial domain data with additive properties. Mellin's domain suits logarithmic scaling problems, while Fourier optimally addresses linear, periodic, or oscillatory domains.
Frequency and Scale Analysis: A Comparative Perspective
The Mellin transform excels in scale analysis by converting multiplicative scale changes into additive shifts, making it ideal for studying signals with varying scale properties, while the Fourier transform is primarily focused on frequency analysis by decomposing signals into sinusoidal components. Fourier transforms represent data in terms of frequency, providing detailed insights into periodic structures, whereas Mellin transforms analyze scaling behaviors, helpful in applications like image processing and fractal analysis. Both transforms offer complementary perspectives: Fourier for periodicity and Mellin for self-similarity and scale invariance in signals.
Transform Properties and Theoretical Foundations
The Mellin transform converts functions by scaling the input variable, making it well-suited for analyzing multiplicative structures and scale-invariant phenomena, while the Fourier transform decomposes functions into sinusoidal components, focusing on frequency content and shift invariance. The Mellin transform integrates a function multiplied by a power function of its variable, linking to complex analysis and the gamma function, contrasting with the Fourier transform's integration against complex exponentials tied to the Laplace transform and group theory. Both transforms share linearity and inversion properties but differ fundamentally in their treatment of dilation versus translation symmetries, reflecting their distinct theoretical foundations in harmonic analysis.
Computational Complexity and Implementation
The Mellin transform exhibits higher computational complexity than the Fourier transform due to its integration over logarithmic scales and its inherent difficulty with fast algorithm development. Fourier transform benefits from the Fast Fourier Transform (FFT) algorithm, reducing complexity from O(N2) to O(N log N), which facilitates efficient implementation in digital signal processing and various engineering applications. Implementing the Mellin transform often requires specialized numerical methods or approximations, limiting its widespread use compared to the Fourier transform's well-established, optimized libraries and hardware support.
Common Use Cases in Signal Processing
The Mellin transform is primarily used in scale-invariant signal analysis, making it suitable for applications like image scaling, pattern recognition, and radar signal analysis where scale changes occur. The Fourier transform excels in frequency analysis, filtering, and time-frequency signal processing tasks such as audio processing, communications, and vibration analysis. Both transforms complement each other by addressing different aspects of signal characterization: Mellin focuses on scale variations, while Fourier emphasizes frequency content.
Strengths and Limitations of Each Transform
The Mellin transform excels at analyzing scale-invariant features and multiplicative processes, making it ideal for applications like image scaling and fractal analysis, but it is less intuitive for periodic or time-domain signals. The Fourier transform provides powerful frequency-domain analysis for linear and time-invariant systems, widely used in signal processing and communications, yet it struggles with non-stationary signals and scaling phenomena. Each transform's mathematical framework dictates its optimal use cases, with Mellin favoring scale-based analysis and Fourier excelling in frequency and harmonic decomposition.
Choosing the Right Transform: Practical Guidelines
Choosing between the Mellin transform and the Fourier transform depends on the problem's nature and data properties. The Mellin transform excels in scaling and multiplicative convolution analysis, making it ideal for size-invariant pattern recognition and image processing. The Fourier transform is preferable for analyzing frequency content and linear time-invariant systems, widely used in signal processing and communications where additive properties dominate.
Mellin transform Infographic
 libterm.com
libterm.com