Coinitial provides a comprehensive suite of cloud communication solutions designed to enhance business connectivity and customer engagement. Their services include cloud telephony, contact center platforms, and collaboration tools tailored to improve operational efficiency and drive growth. Explore the rest of the article to discover how Coinitial can transform Your communication strategy and boost performance.
Table of Comparison
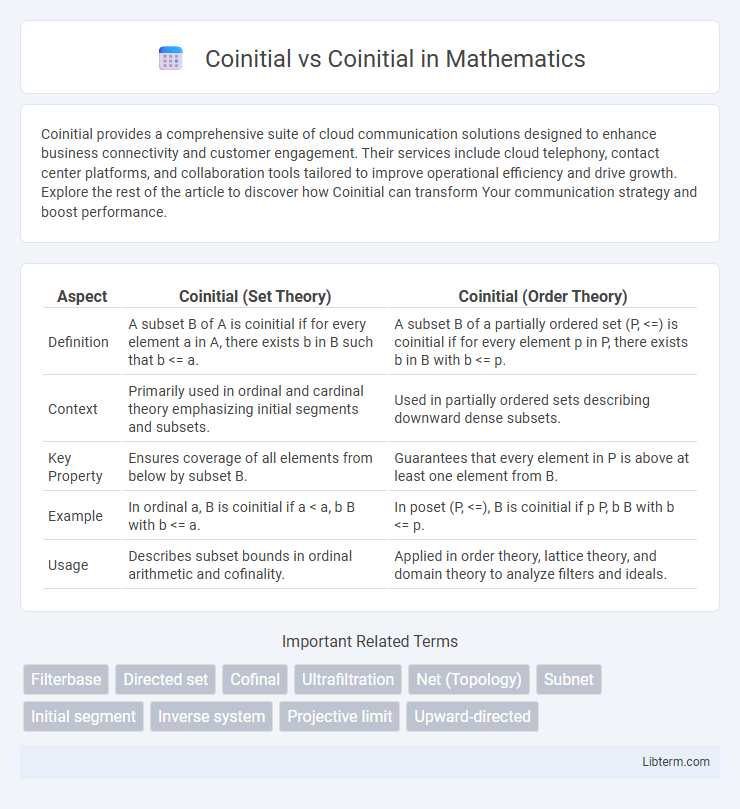
| Aspect | Coinitial (Set Theory) | Coinitial (Order Theory) |
|---|---|---|
| Definition | A subset B of A is coinitial if for every element a in A, there exists b in B such that b <= a. | A subset B of a partially ordered set (P, <=) is coinitial if for every element p in P, there exists b in B with b <= p. |
| Context | Primarily used in ordinal and cardinal theory emphasizing initial segments and subsets. | Used in partially ordered sets describing downward dense subsets. |
| Key Property | Ensures coverage of all elements from below by subset B. | Guarantees that every element in P is above at least one element from B. |
| Example | In ordinal a, B is coinitial if a < a, b B with b <= a. | In poset (P, <=), B is coinitial if p P, b B with b <= p. |
| Usage | Describes subset bounds in ordinal arithmetic and cofinality. | Applied in order theory, lattice theory, and domain theory to analyze filters and ideals. |
Understanding Coinitial: Definition and Meaning
Coinitial refers to two or more geometric figures that share the same initial point or origin, a concept commonly used in geometry and vector analysis. Understanding coinitiality helps in analyzing spatial relationships and directional properties when multiple lines or rays converge at a single point. This concept is fundamental in proving geometric theorems and solving vector problems involving angles and distances from a common vertex.
Coinitial vs Coinitial: Clarifying the Confusion
Coinitial and coincident both describe points or lines occupying the same position, but coinitial specifically refers to rays or segments sharing a common starting point, whereas coincident indicates complete overlap of geometric elements. Understanding the distinction clarifies that two rays are coinitial if they originate from the same endpoint, while coincident lines lie exactly on top of each other throughout their lengths. This precision in terminology helps avoid confusion in geometric proofs and constructions.
Coinitial in Set Theory: Key Concepts
Coinitial in set theory refers to a subset within a partially ordered set (poset) that intersects every nonempty initial segment, ensuring that for every element in the poset, there exists an element in the coinitial subset below it. This property is crucial for understanding dense orderings and the structure of ideals in ordered sets. In contrast, while both coinitial and cofinal subsets relate to order theory, coinitial subsets deal specifically with downward closure and intersections with initial segments, framing fundamental concepts in the analysis of posets and lattices.
Coinitial in Mathematics: Common Applications
Coinitial in mathematics refers to two elements in a partially ordered set that share a common lower bound, playing a crucial role in lattice theory and order theory. This concept is frequently applied in analyzing convergence of nets and filters in topology, where coinitial sets help characterize limits and continuity. In algebra, coinitial elements assist in understanding ideals and substructures by identifying elements that maintain specific order relationships within algebraic systems.
The Role of Coinitial in Order Theory
Coinitial in order theory refers to a subset of a partially ordered set (poset) that intersects every cofinal subset, playing a crucial role in the structure and analysis of posets by ensuring coverage of all significant elements above. This property helps in understanding minimal bounds and the behavior of directed sets, making coinitial subsets foundational in lattice theory and the study of ideal completions. By contrast, the term "coinitial" applied differently or redundantly often leads to confusion, emphasizing the importance of its precise definition within order-theoretic contexts.
Differences and Similarities between Coinitial Concepts
Coinitial concepts share the core principle of originating simultaneously from a common point, emphasizing their simultaneous or concurrent nature in various contexts. Differences arise in specific applications, where Coinitial in geometry refers to rays or lines having the same initial point, while in linguistics or semantics, it may denote ideas or events emerging at the same starting time. Both interpretations maintain the foundational idea of a shared origin, but their usage varies across disciplines, highlighting the conceptual overlap and contextual distinctions.
Common Misconceptions about Coinitial
Common misconceptions about coinitial often confuse it with coincident or concurrent, but coinitial specifically refers to two or more functions or sequences that share the same initial segment or starting point. Another misunderstanding is that coinitial implies identical behavior over the entire domain, whereas it strictly concerns agreement only at the beginning. Clarifying this helps distinguish coinitiality from full equivalence or coincidence in mathematical and computational contexts.
Practical Examples of Coinitial Usage
Coinitial points are essential in geometric constructions where multiple lines or segments originate from a single vertex, such as the concurrent medians of a triangle intersecting at the centroid. Practical examples include determining the center of an angle formed by rays that are coinitial, which helps in angle bisector problems. In coordinate geometry, identifying coinitial vectors simplifies vector addition and subtraction by placing them at the same origin for accurate calculations.
Importance of Coinitial in Advanced Mathematics
Coinitial sets play a crucial role in advanced mathematics, particularly in order theory and lattice theory, by ensuring every element has a corresponding element within the set that is less than or equal to it. This property is essential for analyzing directed sets, filters, and completeness conditions in posets, which are foundational for topology and domain theory. Recognizing coinitial subsets aids in simplifying complex mathematical structures, enabling rigorous proofs and facilitating convergence and approximation techniques in analysis.
Summary: Distinguishing Coinitial vs Coinitial
Coinitial refers to two or more geometric objects, such as segments or rays, sharing the same initial point or origin. This property is crucial in geometry when analyzing the relative positioning of figures, often simplifying proofs and constructions. Understanding the concept of coinitiality helps distinguish between different geometric configurations that originate from a common point.
Coinitial Infographic
 libterm.com
libterm.com