The Z-transform is a powerful mathematical tool used in digital signal processing to analyze discrete-time signals and systems by converting sequences into complex frequency domain representations. It simplifies solving difference equations and aids in system stability and frequency response analysis. Explore the rest of the article to deepen your understanding of how the Z-transform can enhance your signal processing projects.
Table of Comparison
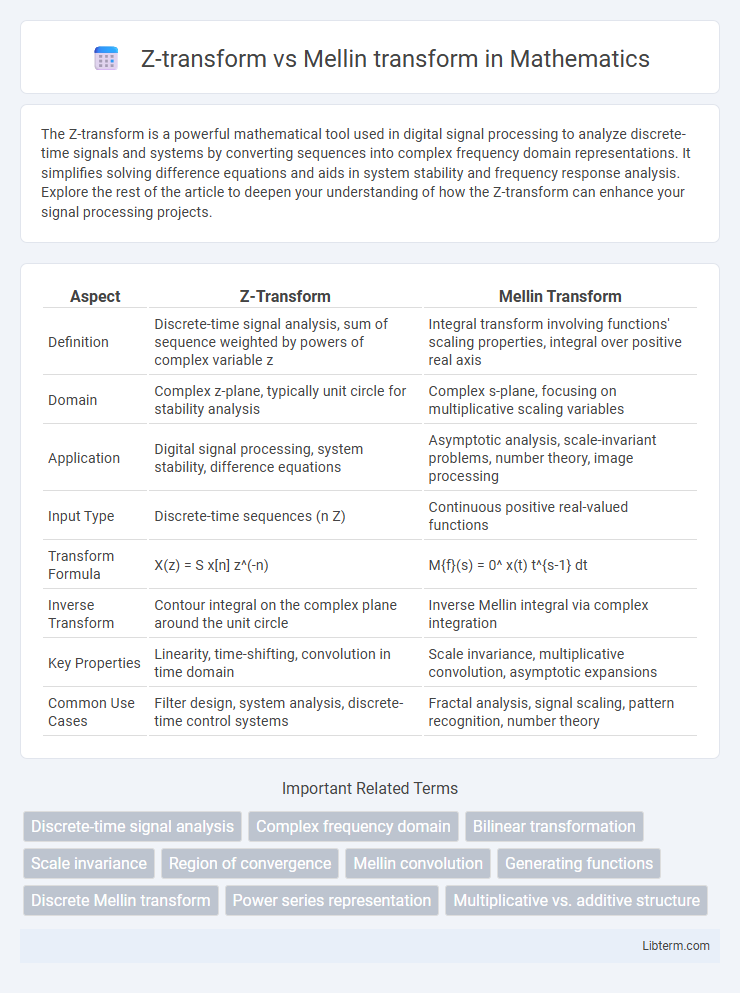
| Aspect | Z-Transform | Mellin Transform |
|---|---|---|
| Definition | Discrete-time signal analysis, sum of sequence weighted by powers of complex variable z | Integral transform involving functions' scaling properties, integral over positive real axis |
| Domain | Complex z-plane, typically unit circle for stability analysis | Complex s-plane, focusing on multiplicative scaling variables |
| Application | Digital signal processing, system stability, difference equations | Asymptotic analysis, scale-invariant problems, number theory, image processing |
| Input Type | Discrete-time sequences (n Z) | Continuous positive real-valued functions |
| Transform Formula | X(z) = S x[n] z^(-n) | M{f}(s) = 0^ x(t) t^{s-1} dt |
| Inverse Transform | Contour integral on the complex plane around the unit circle | Inverse Mellin integral via complex integration |
| Key Properties | Linearity, time-shifting, convolution in time domain | Scale invariance, multiplicative convolution, asymptotic expansions |
| Common Use Cases | Filter design, system analysis, discrete-time control systems | Fractal analysis, signal scaling, pattern recognition, number theory |
Introduction to Z-Transform and Mellin Transform
The Z-transform is a powerful tool used primarily in discrete-time signal processing to convert sequences into complex frequency domain representations, enabling analysis and design of digital filters and systems. The Mellin transform, in contrast, applies to functions defined on positive real numbers and is particularly useful in scale-invariant problems, image analysis, and asymptotic evaluations by transforming multiplicative scaling into additive shifts in the transform domain. Both transforms serve as integral transforms with distinct kernels and applications, where the Z-transform uses powers of a complex variable z and the Mellin transform integrates with a kernel involving power functions of the input variable.
Fundamental Concepts of Z-Transform
The Z-transform is a discrete-time counterpart of the Laplace transform, mapping sequences into the complex frequency domain, essential for analyzing linear, time-invariant systems in digital signal processing. Its fundamental concept revolves around representing sequences as power series in a complex variable \( z \), enabling the study of system stability, frequency response, and difference equation solutions. In contrast, the Mellin transform is primarily used for scale-invariant analysis, focusing on multiplicative scaling properties rather than time shifts, making it less common for discrete signal time-domain processing.
Core Principles of Mellin Transform
The Mellin transform operates by converting a function into a complex frequency domain via integration, emphasizing scale-invariant properties through multiplicative scaling rather than the additive shifts used in the Z-transform. Core principles include the transformation of functions based on powers of the input variable, enabling it to analyze signals and systems with scaling characteristics, making it ideal for applications in fractal analysis and pattern recognition. Unlike the Z-transform, which primarily addresses discrete-time signals and stability via poles and zeros within the unit circle, the Mellin transform handles continuous data and focuses on scale invariance and logarithmic relationships in the input.
Mathematical Definitions and Formulations
The Z-transform is defined as \( X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n} \), where \( z \) is a complex variable, primarily used for analyzing discrete-time signals and systems in the complex frequency domain. The Mellin transform is defined as \( M(s) = \int_0^\infty x(t) t^{s-1} dt \), with \( s \) a complex variable, commonly applied in scale-invariant signal processing and multiplicative convolution analysis. Both transforms convert their respective functions into complex domains, but the Z-transform operates on sequences indexed by integers, whereas the Mellin transform integrates over positive real axes emphasizing scale properties.
Domain of Applications
The Z-transform is widely used in digital signal processing, control systems, and discrete-time system analysis due to its effectiveness in handling sequences and discrete signals. The Mellin transform finds applications primarily in scale-invariant pattern recognition, image analysis, and solving differential equations involving multiplicative scaling. Both transforms serve different domains: Z-transform excels in time-domain discrete systems, while Mellin transform is powerful in fields requiring scale and dilation analysis.
Key Differences in Properties
The Z-transform maps discrete-time signals into the complex frequency domain and is primarily used for analyzing linear, time-invariant discrete systems, leveraging properties like time-shifting and convolution to facilitate digital signal processing. The Mellin transform, by contrast, operates on continuous functions and is scale-invariant, making it particularly suited for analyzing signals with multiplicative scale changes and image processing tasks. Key differences include the Z-transform's emphasis on discrete sequences and stability analysis in the unit circle, whereas the Mellin transform focuses on scale-invariant features by transforming the function into a logarithmic frequency domain.
Advantages and Limitations
The Z-transform offers strong advantages in analyzing discrete-time signals and systems, particularly in stability assessment and digital filter design, with its ability to handle causal sequences and implement easily via difference equations. Its limitation lies in its dependence on discrete-time data and less effectiveness for continuous-scale problems or scale-invariant systems. Conversely, the Mellin transform excels in scale-invariant analysis and multiplicative convolution, widely used in image processing and fractal analysis, but it is constrained by more complex implementation and less intuitive frequency domain interpretation for discrete-time signals.
Use Cases in Signal Processing
The Z-transform is widely used in digital signal processing for analyzing discrete-time systems, stability, and filtering, making it essential in designing digital filters and control systems. The Mellin transform excels in scale-invariant signal analysis and pattern recognition, particularly for applications involving multiplicative scaling such as image processing and radar signal analysis. Both transforms complement each other by addressing different aspects of signal behavior--Z-transform for time-shift properties and Mellin transform for scale-invariant features.
Comparative Analysis in System Analysis
The Z-transform excels in discrete-time signal processing by analyzing system stability and frequency response through complex variable mapping within the unit circle, making it ideal for digital filter design. In contrast, the Mellin transform is powerful for scale-invariant system analysis, particularly in image processing and fractal pattern recognition, due to its ability to convert scaling operations into shifts in the transform domain. Comparative analysis highlights the Z-transform's strength in time-shift and convolution handling for linear, time-invariant discrete systems, while the Mellin transform specializes in multiplicative scaling and dilation properties, offering complementary tools for distinct system analysis challenges.
Conclusion and Future Perspectives
Z-transform excels in discrete-time signal analysis and digital filter design due to its ability to handle sequences and stability regions effectively. Mellin transform offers distinct advantages in scale-invariant feature extraction and image processing, making it well-suited for applications involving multiplicative scaling and pattern recognition. Future research may explore hybrid approaches combining Z-transform's discrete-time capabilities with Mellin transform's scale invariance to enhance multidimensional signal processing and machine learning algorithms.
Z-transform Infographic
 libterm.com
libterm.com