A subring is a subset of a ring that itself forms a ring under the same operations of addition and multiplication. It must contain the additive identity and be closed under subtraction and multiplication to qualify as a subring. Explore the rest of this article to understand the properties and examples of subrings in detail.
Table of Comparison
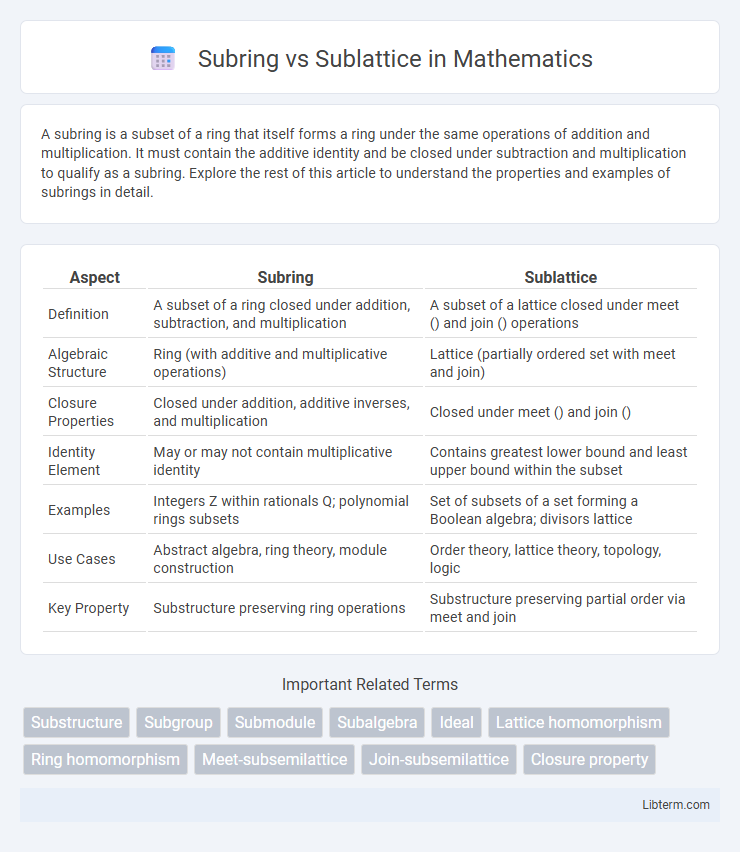
| Aspect | Subring | Sublattice |
|---|---|---|
| Definition | A subset of a ring closed under addition, subtraction, and multiplication | A subset of a lattice closed under meet () and join () operations |
| Algebraic Structure | Ring (with additive and multiplicative operations) | Lattice (partially ordered set with meet and join) |
| Closure Properties | Closed under addition, additive inverses, and multiplication | Closed under meet () and join () |
| Identity Element | May or may not contain multiplicative identity | Contains greatest lower bound and least upper bound within the subset |
| Examples | Integers Z within rationals Q; polynomial rings subsets | Set of subsets of a set forming a Boolean algebra; divisors lattice |
| Use Cases | Abstract algebra, ring theory, module construction | Order theory, lattice theory, topology, logic |
| Key Property | Substructure preserving ring operations | Substructure preserving partial order via meet and join |
Introduction to Subrings and Sublattices
Subrings are subsets of rings that themselves satisfy the ring axioms, including closure under addition, multiplication, and additive inverses, forming a smaller ring within a larger algebraic structure. Sublattices are subsets of lattices that maintain lattice operations meet and join, preserving order-theoretic properties such as associativity, commutativity, and absorption within the partial order framework. Understanding subrings and sublattices requires analyzing their structural properties to identify the preservation of algebraic and order-theoretic operations respectively.
Fundamental Definitions
A subring is a subset of a ring that is itself a ring under the same addition and multiplication operations, requiring closure under addition, multiplication, and the presence of the additive identity. A sublattice is a subset of a lattice that is closed under the lattice operations of meet (greatest lower bound) and join (least upper bound), preserving the partial order structure. While subrings emphasize algebraic properties of addition and multiplication in ring theory, sublattices focus on order-theoretic properties within lattice theory.
Algebraic Structures: Ring vs Lattice
A subring is a subset of a ring that itself forms a ring under the same addition and multiplication operations, preserving ring axioms including associativity, distributivity, and the presence of additive identity and inverses. A sublattice, in contrast, is a subset of a lattice that remains closed under the lattice operations of meet (greatest lower bound) and join (least upper bound), maintaining the lattice properties of idempotence, commutativity, and absorption. While subrings focus on algebraic structures with two binary operations modeled by rings, sublattices emphasize order-theoretic structures characterized by partially ordered sets and their suprema and infima.
Properties of Subrings
Subrings are subsets of rings that themselves satisfy ring axioms, including closure under addition, multiplication, and additive inverses, whereas sublattices focus on order-theoretic structures within lattices. Key properties of subrings include containing the multiplicative identity if the ring is unital, being closed under ring multiplication, and additive inverses, ensuring the subring forms a ring in its own right. Unlike sublattices, subrings emphasize algebraic operations and structures, making them fundamental in ring theory and algebraic structures analysis.
Properties of Sublattices
Sublattices inherit idempotent, commutative, and associative properties of meet and join operations from their parent lattices, ensuring closure under these operations. They preserve the partial order structure, allowing the transfer of lattice-theoretic concepts such as bounds, infima, and suprema within the sublattice. Unlike subrings, which require preservation of ring addition and multiplication, sublattices focus solely on maintaining lattice operations and order relations.
Key Differences Between Subring and Sublattice
A subring is a subset of a ring that is closed under ring operations--addition, subtraction, and multiplication--and contains the multiplicative identity when defined, whereas a sublattice is a subset of a lattice closed under the meet and join operations, focusing on order-theoretic structures. The key difference lies in algebraic structure: subrings pertain to algebraic systems with two binary operations and additive inverses, while sublattices involve partially ordered sets with idempotent, commutative, and associative meet and join. Subrings require the presence of additive inverses and multiplication, making them richer algebraic structures compared to sublattices, which emphasize order and lattice-theoretic properties.
Examples of Subrings in Mathematics
Subrings in mathematics include the set of even integers within the ring of all integers, showcasing closure under addition and multiplication while containing the additive identity zero. The set of all polynomials with integer coefficients forms a subring within the ring of polynomials with real coefficients, demonstrating the preservation of ring operations and a shared multiplicative identity. In matrix theory, the collection of upper triangular matrices with real entries constitutes a subring of the full ring of n-by-n real matrices, maintaining structure under matrix addition and multiplication.
Examples of Sublattices in Mathematics
Examples of sublattices in mathematics include subsets of the integer lattice Z^n that preserve the meet and join operations under componentwise minimum and maximum. For instance, the set of all integer points in a plane forming a grid that is closed under coordinatewise min and max forms a sublattice of Z^2. Unlike subrings, which require closure under addition and multiplication, sublattices emphasize order-theoretic structure within partially ordered sets or lattices.
Applications in Abstract Algebra
Subrings and sublattices serve distinct roles in abstract algebra, with subrings primarily used in ring theory to study algebraic structures equipped with two binary operations--addition and multiplication--preserving ring axioms within subsets. Sublattices, arising in lattice theory, focus on order structures by maintaining meet and join operations within subsets, crucial for analyzing partially ordered sets and their algebraic properties. Applications of subrings include constructing ideals and factor rings, while sublattices facilitate the investigation of algebraic lattices, modular lattices, and their role in universal algebra and logic.
Conclusion: Choosing Between Subring and Sublattice
Choosing between a subring and a sublattice depends on the algebraic structure and the operations involved; subrings require closure under addition, multiplication, and additive inverses while sublattices focus on closure under meet and join operations in lattice theory. For ring theory applications involving both additive and multiplicative structures, subrings provide a more robust framework. In contrast, sublattices are preferred in order theory and lattice-based structures where the emphasis is on ordering and combination rather than ring operations.
Subring Infographic
 libterm.com
libterm.com