A valuation ring is a type of integral domain that plays a crucial role in algebraic geometry and number theory by providing a way to measure the divisibility of elements within a field. It ensures that for every element in the field, either the element or its inverse belongs to the ring, allowing a total ordering based on valuation. Explore the rest of the article to understand how valuation rings influence modern mathematics and their applications in your studies or research.
Table of Comparison
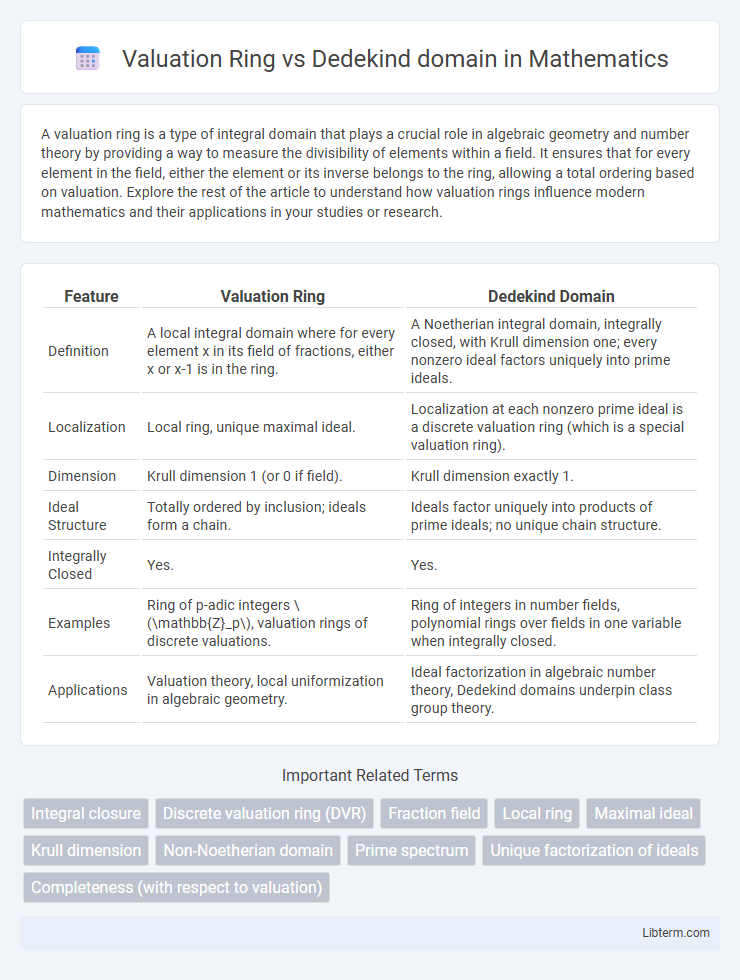
| Feature | Valuation Ring | Dedekind Domain |
|---|---|---|
| Definition | A local integral domain where for every element x in its field of fractions, either x or x-1 is in the ring. | A Noetherian integral domain, integrally closed, with Krull dimension one; every nonzero ideal factors uniquely into prime ideals. |
| Localization | Local ring, unique maximal ideal. | Localization at each nonzero prime ideal is a discrete valuation ring (which is a special valuation ring). |
| Dimension | Krull dimension 1 (or 0 if field). | Krull dimension exactly 1. |
| Ideal Structure | Totally ordered by inclusion; ideals form a chain. | Ideals factor uniquely into products of prime ideals; no unique chain structure. |
| Integrally Closed | Yes. | Yes. |
| Examples | Ring of p-adic integers \(\mathbb{Z}_p\), valuation rings of discrete valuations. | Ring of integers in number fields, polynomial rings over fields in one variable when integrally closed. |
| Applications | Valuation theory, local uniformization in algebraic geometry. | Ideal factorization in algebraic number theory, Dedekind domains underpin class group theory. |
Introduction to Valuation Rings and Dedekind Domains
Valuation rings are integral domains characterized by a totally ordered set of ideals, providing a local framework to study divisibility and valuation functions within a field. Dedekind domains, important in algebraic number theory, are Noetherian integral domains where every nonzero ideal factors uniquely into prime ideals, enabling a structured approach to ideal class groups and factorization. Both valuation rings and Dedekind domains serve as fundamental tools in algebraic geometry and number theory, with valuation rings often serving as localizations of Dedekind domains at prime ideals.
Fundamental Definitions
A valuation ring is an integral domain where for every element in its field of fractions, either the element or its inverse lies in the ring, characterizing a total ordering on divisibility. A Dedekind domain is an integral domain that is Noetherian, integrally closed, and has Krull dimension one, ensuring unique factorization of ideals into prime ideals. While valuation rings emphasize local valuation properties and linear ordering of ideals, Dedekind domains generalize factorization properties in rings of algebraic integers with broader structural conditions.
Key Properties of Valuation Rings
Valuation rings are integral domains characterized by the property that for every element in their field of fractions, either the element or its inverse lies in the ring, making them local and totally ordered by inclusion. They exhibit a well-defined valuation function that measures the divisibility of elements, leading to a valuation group that provides a rich structure for analyzing algebraic extensions and integral closures. Unlike Dedekind domains, which are Noetherian, integrally closed domains with dimension one and factorization into prime ideals, valuation rings may fail Noetherianity but retain important ideal-theoretic properties crucial for valuation theory and local uniformization.
Core Characteristics of Dedekind Domains
Dedekind domains are integral domains characterized by being Noetherian, integrally closed, and having Krull dimension one, which ensures every nonzero ideal factors uniquely into prime ideals. In contrast, valuation rings are local domains where every element or its inverse lies within the ring, reflecting total divisibility and producing a valuation that orders elements. The core characteristics of Dedekind domains emphasize ideal factorization and arithmetic structure, while valuation rings focus on valuation-theoretic properties related to divisibility and localization.
Structural Differences Between Valuation Rings and Dedekind Domains
Valuation rings are local integral domains characterized by a total ordering on their ideals, resulting in a unique maximal ideal and a valuation function that measures divisibility. Dedekind domains are Noetherian integral domains with dimension one, where every nonzero ideal factors uniquely into prime ideals, providing a more global arithmetic structure. The key structural difference lies in the valuation ring's total ordering and local nature versus Dedekind domains' Noetherian property and ideal factorization in a higher-level algebraic context.
Inclusion Relationships and Overlaps
A valuation ring is an integral domain in which for every element in its field of fractions, either the element or its inverse belongs to the ring, emphasizing a total ordering of ideals, while a Dedekind domain is a Noetherian integrally closed domain with dimension one and every nonzero prime ideal maximal. Every valuation ring is a local domain and integrally closed, often appearing as localizations of Dedekind domains at prime ideals, illustrating an inclusion relationship where valuation rings localize the global structure of Dedekind domains. The overlap occurs since valuation rings can serve as local models, capturing the discrete valuation properties present in Dedekind domains, thus linking the two concepts through their shared focus on ideal structure and integral closure.
Examples Illustrating Each Concept
A valuation ring is exemplified by the ring of p-adic integers, which provides a local ring structure crucial in number theory, while a Dedekind domain can be illustrated by the ring of integers in a number field, such as the ring of integers in the quadratic field Q(-5). Valuation rings are characterized by their total ordering of ideals, often appearing in valuation theory and algebraic geometry, whereas Dedekind domains generalize unique factorization properties through prime ideal factorization in algebraic number theory. The distinction is highlighted in examples where valuation rings serve as localizations of Dedekind domains at prime ideals, demonstrating their role as basic building blocks in the structure of Dedekind domains.
Applications in Algebraic Number Theory
Valuation rings provide a local perspective on algebraic structures, allowing precise control over divisibility and factorization within number fields, crucial for analyzing completions of number rings and local-global principles. Dedekind domains, characterized by their ideal factorization properties, serve as the foundational class of rings in algebraic number theory, ensuring unique factorization of ideals and facilitating the study of class groups and ideal class numbers. Applications often intertwine these concepts, using valuation rings to examine local properties and Dedekind domains to handle global arithmetic structure in algebraic number fields.
Pros and Cons: Valuation Rings vs Dedekind Domains
Valuation rings provide a local perspective on ring structures with a strong focus on divisibility properties and valuation theory, making them ideal for studying local behavior in algebraic geometry and number theory; however, their lack of global structure limits applications in broader algebraic contexts. Dedekind domains, characterized by ideal factorization into primes, offer a robust framework for global number theory and algebraic number fields, ensuring unique factorization of ideals but not necessarily elements, which can complicate explicit computations. While valuation rings excel in local analysis through a well-defined valuation function, Dedekind domains maintain a balance between local properties and global arithmetic structure, beneficial for ideal class group investigations but sometimes less flexible for valuation-based problems.
Conclusion and Further Reading
Valuation rings, characterized by their total ordering of ideals, serve as local models capturing valuation-theoretic properties, whereas Dedekind domains generalize unique factorization to ideal factorization in Noetherian integrally closed domains of dimension one. The comparison highlights that every valuation ring is a local Dedekind domain, but not all Dedekind domains are valuation rings, emphasizing their roles in algebraic number theory and algebraic geometry. For deeper insight, consult texts like Atiyah and Macdonald's *Introduction to Commutative Algebra* and Neukirch's *Algebraic Number Theory*, which explore these structures' foundational and applied aspects.
Valuation Ring Infographic
 libterm.com
libterm.com