Local businesses play a crucial role in driving community growth and fostering economic stability. By supporting these enterprises, you help sustain jobs, encourage entrepreneurship, and build a stronger neighborhood identity. Explore the rest of the article to discover how local initiatives can benefit your community and enhance your daily life.
Table of Comparison
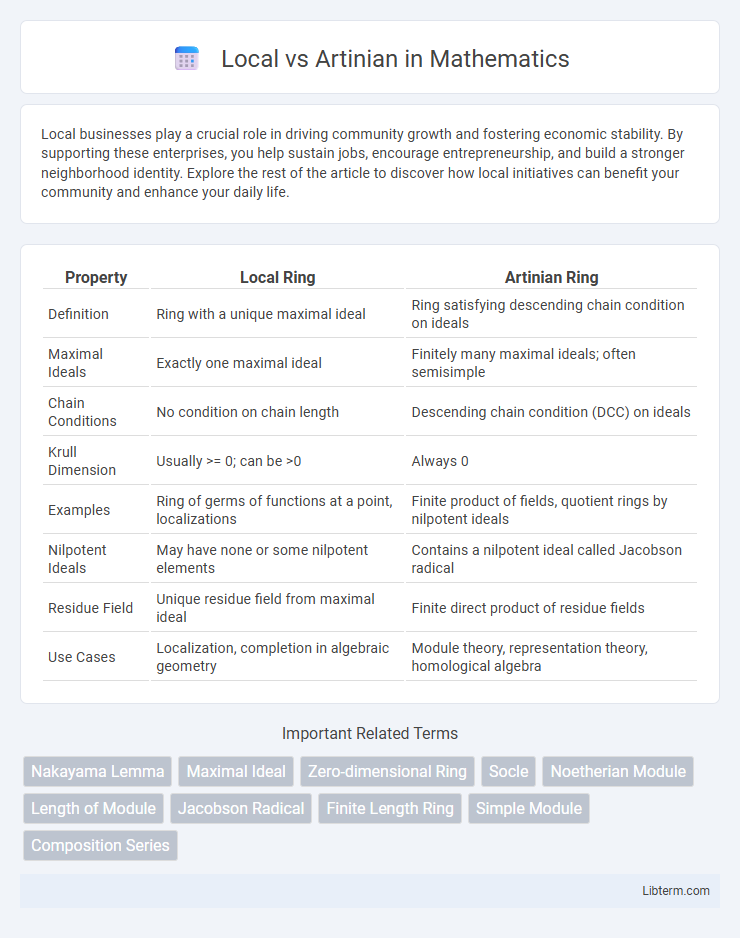
| Property | Local Ring | Artinian Ring |
|---|---|---|
| Definition | Ring with a unique maximal ideal | Ring satisfying descending chain condition on ideals |
| Maximal Ideals | Exactly one maximal ideal | Finitely many maximal ideals; often semisimple |
| Chain Conditions | No condition on chain length | Descending chain condition (DCC) on ideals |
| Krull Dimension | Usually >= 0; can be >0 | Always 0 |
| Examples | Ring of germs of functions at a point, localizations | Finite product of fields, quotient rings by nilpotent ideals |
| Nilpotent Ideals | May have none or some nilpotent elements | Contains a nilpotent ideal called Jacobson radical |
| Residue Field | Unique residue field from maximal ideal | Finite direct product of residue fields |
| Use Cases | Localization, completion in algebraic geometry | Module theory, representation theory, homological algebra |
Introduction to Local and Artinian Rings
Local rings are commutative rings with a unique maximal ideal, crucial in algebraic geometry and commutative algebra for studying local properties of spaces. Artinian rings are characterized by descending chain conditions on ideals, implying they are both Noetherian and of finite length, often decomposing into a finite product of local Artinian rings. Understanding local and Artinian rings provides foundational insight into ring structure, dimension theory, and module decomposition.
Defining Local Rings
Local rings are commutative rings with a unique maximal ideal, enabling a focused study of algebraic structures near a specific point. Artinian rings, characterized by the descending chain condition on ideals, often serve as well-behaved examples of local rings but emphasize finiteness properties. The key distinction lies in the local ring's emphasis on localization at a maximal ideal, while Artinian rings guarantee finiteness and minimal chain complexity.
Defining Artinian Rings
Artinian rings are defined by satisfying the descending chain condition on ideals, ensuring every decreasing sequence of ideals terminates after a finite number of steps. This property distinguishes Artinian rings as they are often zero-dimensional and exhibit well-behaved decompositions into local Artinian rings. Unlike general local rings that are characterized by having a unique maximal ideal, Artinian rings combine finiteness conditions with structural finiteness, enabling comprehensive classification and analysis in algebraic geometry and commutative algebra.
Key Properties of Local Rings
Local rings are characterized by having a unique maximal ideal, which directly influences their residue fields and module theory. They exhibit important properties such as the existence of a nilpotent Jacobson radical and the simplification of factorization structures due to the unique maximal ideal. In contrast, Artinian rings possess descending chain conditions on ideals, ensuring they are both Noetherian and semisimple when reduced, but local rings are not necessarily Artinian unless they satisfy additional finiteness conditions.
Key Properties of Artinian Rings
Artinian rings are characterized by the descending chain condition on ideals, ensuring every descending sequence of ideals stabilizes after finitely many steps. They are always Noetherian when commutative and possess a well-structured decomposition into a finite direct product of Artinian local rings, highlighting their key property of having a finite length as modules over themselves. Unlike local rings, which have a unique maximal ideal, Artinian rings can have multiple maximal ideals but maintain a finite length and a semisimple structure on their Jacobson radical quotient.
Similarities Between Local and Artinian Rings
Local and Artinian rings both possess a unique maximal ideal, which governs their algebraic structure, making them pivotal in commutative algebra and algebraic geometry. Both types of rings exhibit the descending chain condition on ideals, ensuring that every non-empty set of ideals has a minimal element, which simplifies their module theory. These shared properties facilitate the study of singularities and decomposition of modules, highlighting their foundational roles in ring theory.
Major Differences: Local vs Artinian Rings
Local rings are characterized by having a unique maximal ideal, making them essential in algebraic geometry and commutative algebra for studying local properties of spaces. Artinian rings satisfy the descending chain condition on ideals, ensuring that every descending sequence of ideals eventually stabilizes, which implies that Artinian rings have finite length as modules over themselves. A major difference lies in their structure: local rings emphasize uniqueness of maximal ideals while Artinian rings highlight finiteness conditions, and although many Artinian rings are local, not all local rings are Artinian.
Examples of Local and Artinian Rings
Examples of local rings include the ring of formal power series \(k[[x]]\) over a field \(k\) and the localization of a commutative ring \(R\) at a prime ideal \(P\), denoted \(R_P\). Artinian rings are exemplified by finite-dimensional algebras over a field, such as matrix rings over a field or the ring \(k[x]/(x^n)\), where \(k\) is a field and \(n\) is a positive integer. Every Artinian local ring is both local and satisfies the descending chain condition on ideals, while not all local rings are Artinian.
Applications in Algebra and Module Theory
Local rings play a crucial role in algebra and module theory by providing a framework for studying modules with unique maximal ideals, which simplifies localization and structure analysis. Artinian rings, characterized by descending chain conditions on ideals, are essential in understanding modules of finite length and decompositions into simple submodules. The interplay between local and Artinian rings facilitates classification problems, representation theory, and homological dimensions in algebraic systems.
Summary: Choosing Between Local and Artinian
Local rings have a unique maximal ideal and are crucial in algebraic geometry and commutative algebra for studying local properties of spaces. Artinian rings are characterized by descending chain conditions on ideals, ensuring a finite length and decomposition into simple modules. Choosing between local and Artinian rings depends on the context: local rings suit local analysis and dimension theory, while Artinian rings are ideal for understanding finite-dimensional algebraic structures and representation theory.
Local Infographic
 libterm.com
libterm.com