Ultrametric spaces feature a strong form of the triangle inequality, where the distance between two points is always less than or equal to the maximum of the distances connecting them through a third point. This concept is fundamental in various fields such as p-adic analysis, hierarchical clustering, and evolutionary biology, providing a framework to model branching structures and nested relationships. Explore the rest of the article to understand how ultrametrics shape complex data analysis and mathematical theories.
Table of Comparison
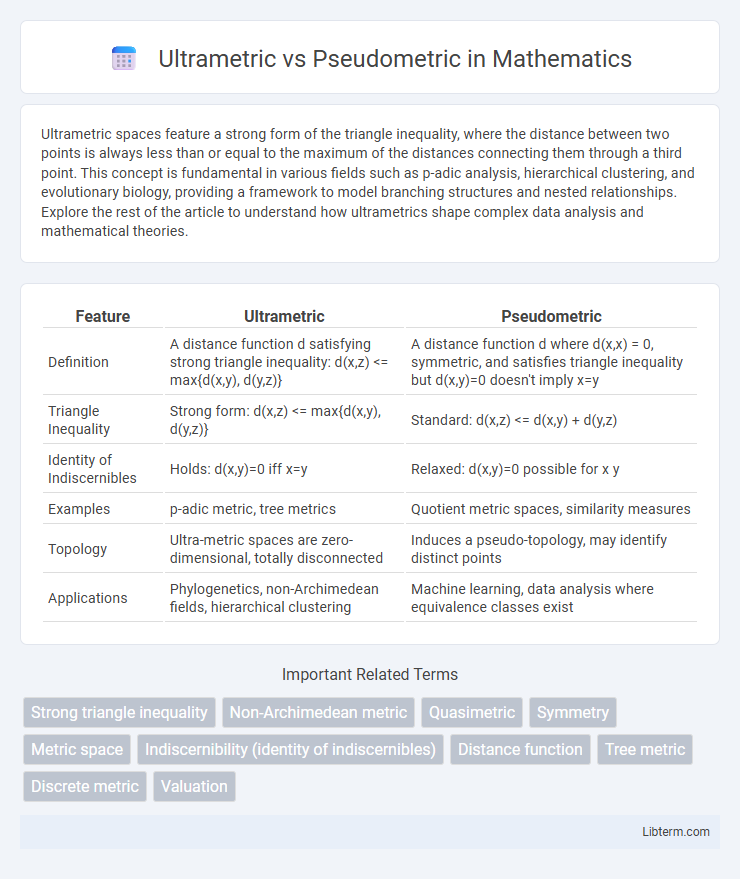
| Feature | Ultrametric | Pseudometric |
|---|---|---|
| Definition | A distance function d satisfying strong triangle inequality: d(x,z) <= max{d(x,y), d(y,z)} | A distance function d where d(x,x) = 0, symmetric, and satisfies triangle inequality but d(x,y)=0 doesn't imply x=y |
| Triangle Inequality | Strong form: d(x,z) <= max{d(x,y), d(y,z)} | Standard: d(x,z) <= d(x,y) + d(y,z) |
| Identity of Indiscernibles | Holds: d(x,y)=0 iff x=y | Relaxed: d(x,y)=0 possible for x y |
| Examples | p-adic metric, tree metrics | Quotient metric spaces, similarity measures |
| Topology | Ultra-metric spaces are zero-dimensional, totally disconnected | Induces a pseudo-topology, may identify distinct points |
| Applications | Phylogenetics, non-Archimedean fields, hierarchical clustering | Machine learning, data analysis where equivalence classes exist |
Introduction to Ultrametric and Pseudometric Spaces
Ultrametric spaces are specialized metric spaces where the distance function satisfies a stronger version of the triangle inequality, known as the ultrametric inequality: for any points x, y, z, the distance d(x, z) <= max{d(x, y), d(y, z)}. Pseudometric spaces generalize metric spaces by allowing distinct points to have zero distance, relaxing the separation axiom while preserving non-negativity, symmetry, and the triangle inequality. These foundational concepts play a crucial role in topology, analysis, and applications such as p-adic number theory and hierarchical clustering.
Defining Key Concepts: Metrics, Pseudometrics, and Ultrametrics
Metrics define a distance function that satisfies non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. Pseudometrics relax the identity of indiscernibles, allowing distinct points to have zero distance, preserving all other metric properties. Ultrametrics strengthen the triangle inequality to an ultrametric inequality, where the distance between two points is at most the maximum of their distances to a third point, creating a hierarchical clustering structure.
Mathematical Properties of Ultrametric Spaces
Ultrametric spaces satisfy a stronger form of the triangle inequality, known as the ultrametric inequality, where for any points x, y, z, the distance d(x, z) <= max{d(x, y), d(y, z)} holds. This property leads to distinctive features such as all triangles being isosceles with the two longer sides equal, and open balls being both open and closed sets, resulting in a highly non-Euclidean topology. In contrast to pseudometrics, ultrametrics enforce a hierarchical clustering structure, making them essential in p-adic analysis, taxonomy, and phylogenetics.
Fundamental Characteristics of Pseudometric Spaces
Pseudometric spaces generalize metric spaces by allowing distinct points to have zero distance, thus relaxing the identity of indiscernibles property. Unlike ultrametric spaces which satisfy the strong triangle inequality \( d(x,z) \leq \max\{d(x,y), d(y,z)\} \), pseudometrics only require the standard triangle inequality \( d(x,z) \leq d(x,y) + d(y,z) \). This fundamental relaxation enables pseudometric spaces to model similarity rather than strict distance, proving useful in contexts like functional analysis and theoretical computer science.
Ultrametric vs Pseudometric: Core Differences
Ultrametrics are a specialized class of pseudometrics characterized by the strong triangle inequality \( d(x,z) \leq \max\{d(x,y), d(y,z)\} \), which is stricter than the standard triangle inequality in pseudometrics. Unlike pseudometrics, ultrametrics often induce hierarchical clustering structures due to their non-Archimedean property, making them essential in fields like taxonomy and phylogenetics. Pseudometrics allow distinct points to have zero distance, but ultrametrics impose a more rigid geometric framework, leading to ultrametric spaces with unique topological and combinatorial properties.
Examples of Ultrametric and Pseudometric Spaces
Ultrametric spaces include the p-adic numbers, where the distance between two numbers reflects their highest power of a prime dividing their difference, clearly satisfying the strong triangle inequality. Pseudometric spaces arise in scenarios like function spaces with a distance defined by the difference in function values, allowing distinct points to have zero distance. These examples highlight that ultrametrics impose a more rigid structure than pseudometrics, ensuring hierarchical clustering in datasets such as evolutionary trees and non-Archimedean geometry.
Applications in Data Analysis and Clustering
Ultrametric spaces are essential in hierarchical clustering, enabling the representation of data with strong nested structures that reflect strict triangle inequality properties, ideal for phylogenetic trees and taxonomy. Pseudometric spaces allow some data points to have zero distance despite being distinct, facilitating clustering in noisy or ambiguous datasets where traditional metrics fail to differentiate small variations. These properties influence the choice of clustering algorithms, such as ultrametric-based dendrogram construction versus pseudometric approaches in soft clustering and dimensionality reduction tasks.
Role in Topology and Geometry
Ultrametrics impose a strong form of the triangle inequality, d(x,z) <= max{d(x,y), d(y,z)}, which significantly shapes the topology by producing totally disconnected, often fractal-like spaces relevant in p-adic analysis and hierarchical clustering. Pseudometrics allow distinct points to have zero distance, enabling the study of quotient spaces and finer equivalence relations in topology, useful in identifying minimal critical points in geometry. The rigidity of ultrametrics fosters non-Archimedean geometry, while pseudometrics facilitate generalized metric structures essential for geometric group theory and functional analysis.
Advantages and Limitations of Each Metric
Ultrametrics provide a strong hierarchical structure ideal for clustering and phylogenetic analysis, ensuring the triangle inequality holds with a maximum distance metric that simplifies data interpretation. Their limitation lies in reduced flexibility, often forcing rigid tree-like representations unsuitable for datasets lacking inherent hierarchical patterns. Pseudometrics offer greater flexibility by allowing zero distance between distinct points, accommodating more general similarity measures but potentially complicating interpretations due to relaxed identity requirements and less structured geometric constraints.
Summary and Future Research Directions
Ultrametric spaces, characterized by a strengthened triangle inequality, facilitate hierarchical clustering and have applications in phylogenetics and p-adic analysis, whereas pseudometric spaces relax the requirement of distinguishability, allowing nonzero distances between identical points and enabling studies in functional analysis and topology. Current research explores metric embedding techniques, generalizations of ultrametrics in data science, and the interplay between pseudometric-induced topologies and convergence properties. Future directions include developing scalable algorithms for ultrametric learning, investigating pseudometric structures in machine learning and network analysis, and extending theoretical frameworks to accommodate complex data hierarchies and uncertainty modeling.
Ultrametric Infographic
 libterm.com
libterm.com