A lattice-ordered group combines the algebraic structure of a group with a lattice order, allowing elements to be compared using both group operations and a partial order that is compatible with the group structure. This blend facilitates advanced analysis in algebra and order theory, particularly in solving inequalities and understanding symmetries within ordered frameworks. Explore the rest of the article to deepen your understanding of how lattice-ordered groups function and their applications.
Table of Comparison
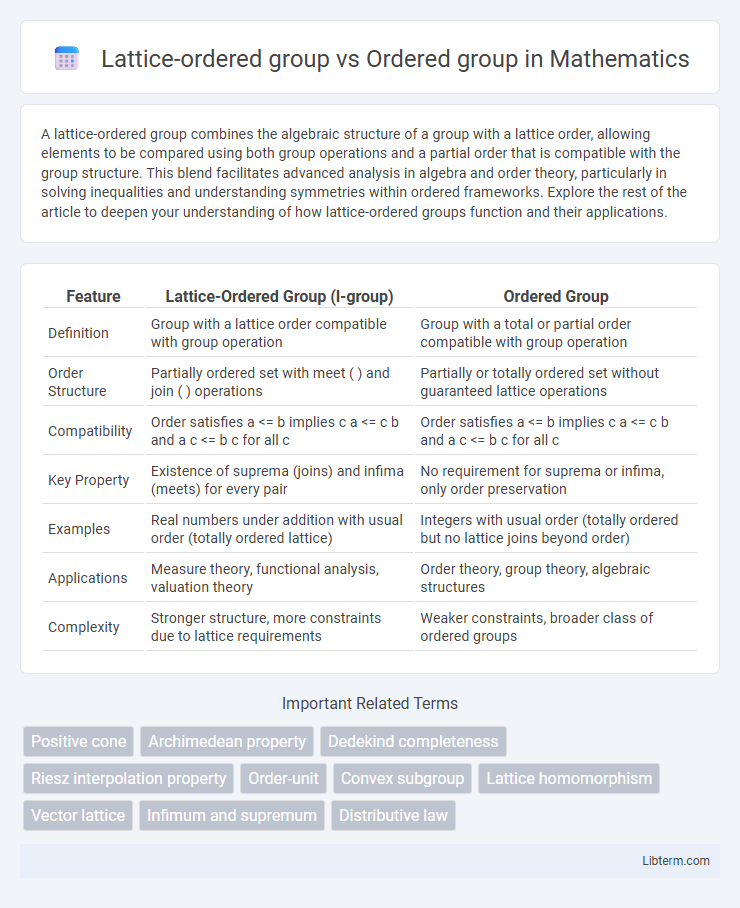
| Feature | Lattice-Ordered Group (l-group) | Ordered Group |
|---|---|---|
| Definition | Group with a lattice order compatible with group operation | Group with a total or partial order compatible with group operation |
| Order Structure | Partially ordered set with meet ( ) and join ( ) operations | Partially or totally ordered set without guaranteed lattice operations |
| Compatibility | Order satisfies a <= b implies c a <= c b and a c <= b c for all c | Order satisfies a <= b implies c a <= c b and a c <= b c for all c |
| Key Property | Existence of suprema (joins) and infima (meets) for every pair | No requirement for suprema or infima, only order preservation |
| Examples | Real numbers under addition with usual order (totally ordered lattice) | Integers with usual order (totally ordered but no lattice joins beyond order) |
| Applications | Measure theory, functional analysis, valuation theory | Order theory, group theory, algebraic structures |
| Complexity | Stronger structure, more constraints due to lattice requirements | Weaker constraints, broader class of ordered groups |
Introduction to Ordered Structures in Algebra
Lattice-ordered groups (l-groups) extend the concept of ordered groups by combining group theory with lattice theory, enabling both algebraic and order-theoretic operations to coexist harmoniously. Unlike ordered groups, which only require a total or partial order compatible with the group operation, lattice-ordered groups possess a lattice order where every pair of elements has a well-defined supremum (join) and infimum (meet). This enriched structure facilitates the study of algebraic systems with intricate order properties, making l-groups central to advanced research in ordered structures within algebra.
Defining Ordered Groups: Key Concepts
Ordered groups are algebraic structures combining a group operation with a total or partial order compatible with the group operation, ensuring order preservation under group multiplication. Lattice-ordered groups (l-groups) extend ordered groups by requiring the order to form a lattice, meaning every pair of elements has both a least upper bound (join) and greatest lower bound (meet). This lattice structure enables more refined comparisons and algebraic manipulations within the group, making l-groups a crucial object of study in order theory and algebra.
Understanding Lattice-Ordered Groups (l-groups)
Lattice-ordered groups (l-groups) are algebraic structures combining group and lattice properties, where every pair of elements has a well-defined least upper bound and greatest lower bound, enhancing the ordered group's framework. Unlike general ordered groups that only require a total or partial order compatible with the group operation, l-groups impose a lattice order, facilitating refined algebraic and order-theoretic analysis. Understanding l-groups involves studying how lattice operations interact with group operations to create a richer structure applicable in areas like functional analysis and mathematical logic.
Fundamental Properties of Ordered Groups
Ordered groups possess a total or partial order compatible with the group operation, ensuring that if \(a \leq b\), then \(ga \leq gb\) for all \(g\) in the group. Lattice-ordered groups (l-groups) extend ordered groups by requiring the order to form a lattice, meaning every pair of elements has both a meet (greatest lower bound) and join (least upper bound). Fundamental properties of ordered groups include translation invariance of the order and the preservation of order under group inverses, with lattice-ordered groups further enabling algebraic manipulations based on lattice operations that enhance structural analysis.
Core Characteristics of Lattice-Ordered Groups
Lattice-ordered groups (l-groups) are algebraic structures combining group operations with a lattice order, ensuring every pair of elements has a well-defined least upper bound (join) and greatest lower bound (meet). The lattice order in l-groups is translation-invariant, meaning that group multiplication preserves order relations, a property not required in general ordered groups. Core characteristics of l-groups include the compatibility of the lattice structure with group operations, existence of lattice bounds for any element pair, and the ability to perform algebraic and order-theoretic operations simultaneously.
Differences Between Ordered Groups and l-Groups
Lattice-ordered groups (l-groups) extend ordered groups by requiring that every pair of elements has both a least upper bound and a greatest lower bound, embedding a lattice structure within the group. Ordered groups only require a total or partial order compatible with the group operation, lacking the guaranteed existence of suprema and infima for arbitrary pairs. This lattice condition in l-groups enables more robust algebraic and order-theoretic properties, distinguishing them from general ordered groups.
Examples Illustrating Ordered Groups
Ordered groups, such as the group of integers \((\mathbb{Z}, +)\) with the usual order, exemplify structures where the group operation is compatible with a total order, ensuring \(a \leq b\) implies \(a + c \leq b + c\) for all \(c\). Lattice-ordered groups extend this concept by requiring the order to be a lattice, where any two elements have a least upper bound and greatest lower bound, with the real numbers \((\mathbb{R}, +, \leq)\) forming a key example of a lattice-ordered group. Concrete examples like the additive integers as an ordered group and the real numbers as a lattice-ordered group highlight the distinction in order structures and their algebraic compatibility.
Examples of Lattice-Ordered Groups in Mathematics
Lattice-ordered groups (l-groups) extend ordered groups by ensuring every pair of elements has a greatest lower bound and least upper bound, exemplified by the group of real-valued continuous functions on a compact space with pointwise order. Another key example is the group of automorphisms of a linearly ordered set preserving the order, forming a lattice structure under composition. These lattice-ordered groups find applications in functional analysis and algebraic topology, highlighting their richer structure compared to general ordered groups.
Applications of Ordered and Lattice-Ordered Groups
Ordered groups facilitate the modeling of hierarchical and temporal structures in computer science, economics, and decision theory by providing a framework where elements maintain a consistent order compatible with group operations. Lattice-ordered groups (l-groups) extend this framework, enabling applications in functional analysis, particularly in the study of Riesz spaces and vector lattices, as well as in algebraic topology and measure theory by supporting both order and algebraic operations simultaneously. The interplay between order and lattice properties in l-groups enhances solutions in optimization problems and provides more refined tools for handling non-linear structures in mathematical physics.
Conclusion: Choosing Between Ordered and Lattice-Ordered Groups
Ordered groups provide a foundational structure with a total or partial order compatible with the group operation, ideal for applications requiring simpler hierarchical relations. Lattice-ordered groups (l-groups) extend ordered groups by integrating lattice operations, enabling the definition of suprema and infima, which supports more complex algebraic and analytical problems. Choosing between ordered and lattice-ordered groups depends on whether the problem requires the additional lattice structure for completeness and richer algebraic behavior or if a basic order suffices for the group dynamics.
Lattice-ordered group Infographic
 libterm.com
libterm.com