A projective set is a concept in descriptive set theory characterized by its definability through projections of Borel sets and closed under operations like complementation and continuous preimages. These sets play a crucial role in understanding the complexities of definable sets in Polish spaces and have applications in real analysis, logic, and theoretical computer science. Explore the rest of the article to dive deeper into the structure and properties of projective sets.
Table of Comparison
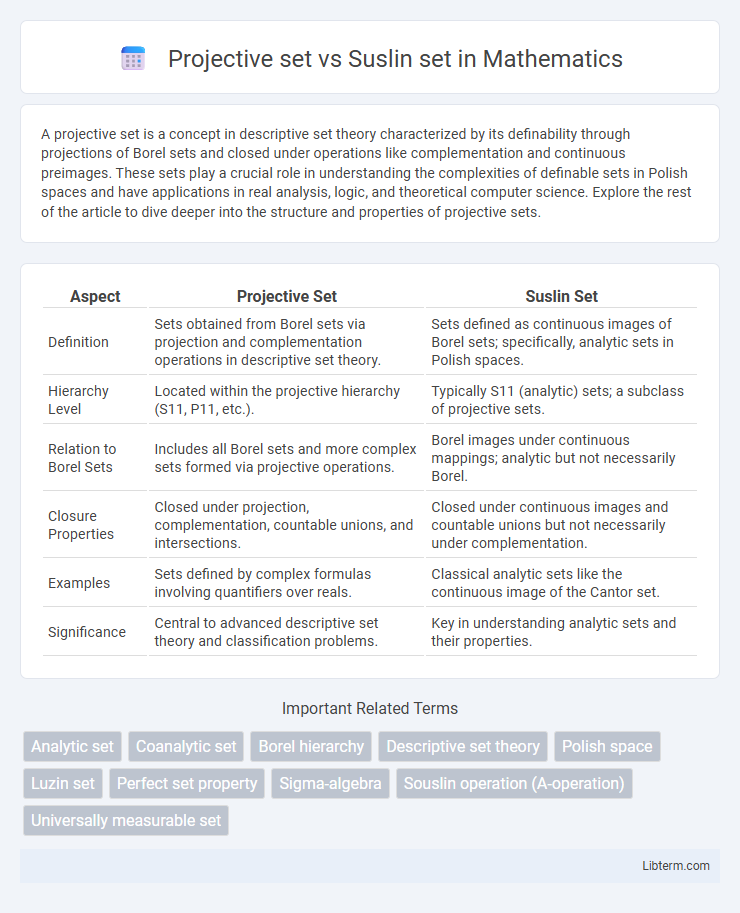
| Aspect | Projective Set | Suslin Set |
|---|---|---|
| Definition | Sets obtained from Borel sets via projection and complementation operations in descriptive set theory. | Sets defined as continuous images of Borel sets; specifically, analytic sets in Polish spaces. |
| Hierarchy Level | Located within the projective hierarchy (S11, P11, etc.). | Typically S11 (analytic) sets; a subclass of projective sets. |
| Relation to Borel Sets | Includes all Borel sets and more complex sets formed via projective operations. | Borel images under continuous mappings; analytic but not necessarily Borel. |
| Closure Properties | Closed under projection, complementation, countable unions, and intersections. | Closed under continuous images and countable unions but not necessarily under complementation. |
| Examples | Sets defined by complex formulas involving quantifiers over reals. | Classical analytic sets like the continuous image of the Cantor set. |
| Significance | Central to advanced descriptive set theory and classification problems. | Key in understanding analytic sets and their properties. |
Introduction to Projective and Suslin Sets
Projective sets are defined through operations of projection and complementation starting from Borel sets, forming a rich hierarchy important in descriptive set theory. Suslin sets, also known as analytic sets, arise as continuous images of Borel sets and represent the first level of complexity beyond Borel sets in this hierarchy. Understanding the distinction between projective and Suslin sets is essential for analyzing definability, complexity, and measurable properties in Polish spaces.
Historical Background and Development
Projective sets, emerging from descriptive set theory in the early 20th century, were initially studied through the works of Luzin and Suslin, who explored their definability and measure properties. Suslin sets, a crucial subclass of analytic sets, were introduced by Mikhail Suslin in 1917, revealing limitations in the classical Borel hierarchy and prompting deeper investigations into projective hierarchies. The development of effective descriptive theory and advances by researchers like Addison and Moschovakis further clarified the structural differences and relationships between projective and Suslin sets within set theory.
Definitions: Projective Sets Explained
Projective sets form a hierarchy of definable sets of real numbers obtained from Borel sets through operations of projection and complementation, starting with analytic sets (S11). A set is projective if it can be constructed using a finite number of projections and complements beginning with Borel sets, encompassing classes such as S11, P11, S21, and so forth. Suslin sets, synonymous with analytic sets or S11 sets, are precisely the continuous images of Borel sets and constitute the first level of the projective hierarchy.
Definitions: Suslin Sets Uncovered
Suslin sets, also known as analytic sets, are defined as continuous images of Borel sets in Polish spaces and can be constructed using Suslin operations on sequences of closed sets. Projective sets form a hierarchy generated from Borel sets through operations of projection and complementation, with Suslin sets corresponding to the first level, denoted as S11. The key distinction lies in Suslin sets being the analytic subsets of Polish spaces, while projective sets encompass higher complexity levels obtained through successive projections and complements.
Hierarchical Structure in Descriptive Set Theory
Projective sets form a hierarchy starting with Borel sets and extending through definability levels like analytic (S11) and coanalytic (P11) sets, structured by operations of projection and complementation. Suslin sets, often identified with analytic sets, occupy the first projective level as projections of Borel sets and highlight the foundational role of continuous images of Polish spaces in the hierarchy. The projective hierarchy elaborates complex definability while Suslin sets anchor this structure, providing a crucial base for understanding higher-level projective classes in descriptive set theory.
Key Properties and Differences
Projective sets are definable through projections and complements starting from Borel sets and include classes like analytic and coanalytic sets, while Suslin sets specifically refer to analytic sets generated by continuous images of Borel sets. Key properties of projective sets include closure under projection, complementation, and countable unions, whereas Suslin sets primarily exhibit closure under continuous images and countable unions but are not closed under complementation. The main difference lies in the broader definability hierarchy of projective sets compared to the narrower analytic category of Suslin sets, impacting their roles in descriptive set theory and measure theory.
Interrelations Between Projective and Suslin Sets
Projective sets arise from operations on Borel sets through projections and complements, forming an increasing hierarchy such as the S^1_n and P^1_n classes, while Suslin sets are precisely the analytic sets obtained as continuous images of Borel sets. The interrelation between projective and Suslin sets reveals that all Suslin sets are S^1_1 projective sets, but higher-level projective sets extend beyond Suslin sets by incorporating complements and iterative projections. Understanding this hierarchy is fundamental in descriptive set theory, as it delineates the complexity and definability of sets within Polish spaces.
Examples and Applications
Projective sets include all definable sets obtained from Borel sets through operations like projection and complementation, with examples such as analytic sets (S11) that arise in descriptive set theory. Suslin sets, a subset of the projective sets, are defined as projections of closed sets and serve as key examples in measure theory and real analysis. Applications of these sets span from effective classification problems in topology to advanced measure-theoretic results in probability and functional analysis.
Importance in Modern Set Theory
Projective sets, defined through projections of Borel sets and closure under operations like continuous images and complements, form a central hierarchy in descriptive set theory, revealing complex structural properties of definable sets of reals. Suslin sets, also known as analytic sets, are the initial level of this hierarchy, serving as foundational examples of non-Borel sets with crucial regularity properties such as measurability and the property of Baire. The study of Projective and Suslin sets drives advances in determinacy axioms and inner model theory, underpinning key results on definability, large cardinals, and the interaction between set theory and real analysis in modern research.
Open Problems and Research Directions
Projective sets form an extensive hierarchy within descriptive set theory, characterized by operations of projection and complementation applied to Borel sets, while Suslin sets specifically denote analytic sets arising as continuous images of Borel sets. Open problems in the study of projective sets include the exploration of regularity properties such as Lebesgue measurability, the perfect set property, and determinacy hypotheses beyond projective levels, especially in the absence of large cardinal axioms. Research directions focus on refining the classification of Suslin sets within larger projective classes, analyzing their structural complexity through effective descriptive set theory, and investigating connections with inner model theory and determinacy principles.
Projective set Infographic
 libterm.com
libterm.com