Complex analysis explores functions of complex variables, revealing intricate behaviors like analyticity, contour integration, and residue theory. Mastery of these concepts unlocks powerful techniques for solving real-world mathematical and engineering problems. Dive into the rest of the article to deepen your understanding of this fascinating field.
Table of Comparison
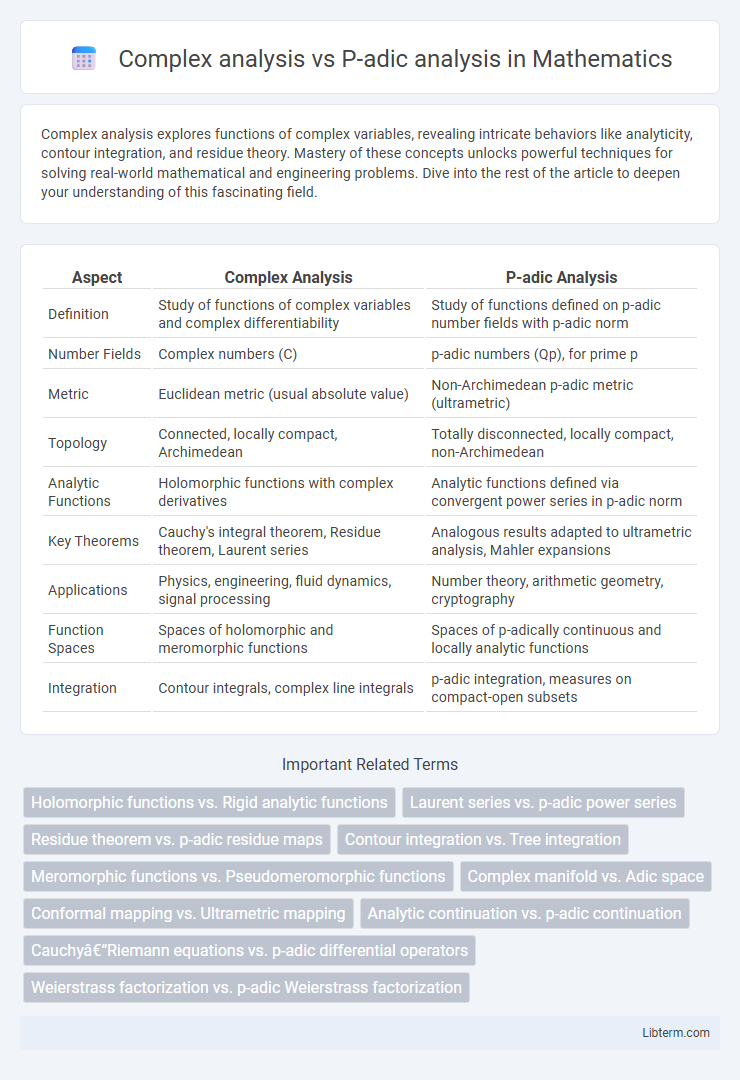
| Aspect | Complex Analysis | P-adic Analysis |
|---|---|---|
| Definition | Study of functions of complex variables and complex differentiability | Study of functions defined on p-adic number fields with p-adic norm |
| Number Fields | Complex numbers (C) | p-adic numbers (Qp), for prime p |
| Metric | Euclidean metric (usual absolute value) | Non-Archimedean p-adic metric (ultrametric) |
| Topology | Connected, locally compact, Archimedean | Totally disconnected, locally compact, non-Archimedean |
| Analytic Functions | Holomorphic functions with complex derivatives | Analytic functions defined via convergent power series in p-adic norm |
| Key Theorems | Cauchy's integral theorem, Residue theorem, Laurent series | Analogous results adapted to ultrametric analysis, Mahler expansions |
| Applications | Physics, engineering, fluid dynamics, signal processing | Number theory, arithmetic geometry, cryptography |
| Function Spaces | Spaces of holomorphic and meromorphic functions | Spaces of p-adically continuous and locally analytic functions |
| Integration | Contour integrals, complex line integrals | p-adic integration, measures on compact-open subsets |
Introduction to Complex and P-adic Analysis
Complex analysis studies functions of complex variables focusing on holomorphic functions, analytic continuation, and contour integration, fundamental in classical mathematics and physics. P-adic analysis explores functions over p-adic number fields, emphasizing non-Archimedean metrics and unique convergence properties, crucial in number theory and algebraic geometry. Both fields analyze functions but differ in their underlying number systems, topology, and applications.
Foundations: Complex Numbers vs. P-adic Numbers
Complex analysis is grounded in the field of complex numbers, which extend the real numbers by introducing the imaginary unit i, enabling a rich geometric interpretation on the complex plane and the study of holomorphic functions. P-adic analysis is based on p-adic numbers, constructed through the completion of rational numbers with respect to the p-adic norm, which measures divisibility by a prime p and leads to a non-Archimedean metric space. The fundamental difference in their foundations--complex numbers forming a continuous Euclidean field versus p-adic numbers creating an ultrametric topology--profoundly influences the structure of functions, convergence, and analytic properties in each domain.
Topological Structures in Both Analyses
Complex analysis explores functions over the complex numbers with a rich topological structure defined by the Euclidean metric, where open sets form a connected, locally compact, and complete metric space. P-adic analysis operates on the field of p-adic numbers, featuring a non-Archimedean ultrametric topology that is totally disconnected, locally compact, and complete, leading to fundamentally different notions of continuity and convergence. These contrasting topologies influence the respective analytic frameworks, with complex analysis relying on connectedness and holomorphic functions, while p-adic analysis leverages the unique, tree-like structure of p-adic spaces for rigid analytic geometry and number-theoretic applications.
Analytic Functions: Definitions and Properties
Analytic functions in complex analysis are defined as functions locally expressible by convergent power series with complex coefficients, exhibiting properties like holomorphy and conformality. In p-adic analysis, analytic functions are similarly expressed via convergent power series but within the non-Archimedean p-adic number field, where convergence and differentiability reflect the ultrametric norm's unique topology. The behavior and structure of analytic functions differ significantly due to the distinct field characteristics, influencing concepts such as continuity, differentiability, and the radius of convergence.
Convergence Concepts: Absolute vs. P-adic Convergence
In complex analysis, convergence is typically studied through absolute convergence, where a series converges if the sum of the absolute values of its terms is finite, ensuring analytic functions have well-defined limits and power series expansions. P-adic analysis employs a non-Archimedean norm, leading to a different notion of convergence where a series converges if its terms tend to zero with respect to the p-adic valuation, emphasizing the ultrametric inequality and often resulting in stronger convergence properties. This fundamental difference highlights how absolute convergence under the usual Euclidean metric contrasts with p-adic convergence governed by the p-adic norm, impacting the behavior of analytic functions in their respective fields.
Integration and Cauchy’s Theorem: Contrasts and Parallels
Complex analysis studies integration of holomorphic functions over contours in the complex plane, where Cauchy's Theorem guarantees that integrals around closed loops vanish when functions are analytic inside the region. P-adic analysis, defined over p-adic fields, involves integration with respect to Haar measures on totally disconnected spaces, lacking classical pathwise integrals and instead relying on measure-theoretic tools. While Cauchy's Theorem has no direct analog in p-adic analysis, parallels arise through rigid analytic spaces and p-adic differential equations, illustrating distinct but related structural roles in each theory.
Applications in Number Theory
Complex analysis provides powerful tools for number theory, including the study of modular forms and L-functions, which are essential for understanding the distribution of prime numbers and solving Diophantine equations. P-adic analysis extends these methods to p-adic numbers, facilitating local-global principles and offering insights into arithmetic geometry, such as the proof of Fermat's Last Theorem through p-adic Galois representations. Both frameworks complement each other by linking analytic properties with algebraic structures to advance modern number theory research.
Notable Theorems: Similarities and Differences
Complex analysis and p-adic analysis both feature foundational theorems such as Cauchy's integral theorem and the residue theorem, adapted to their respective number systems. In complex analysis, these theorems utilize contour integration in the complex plane, while p-adic analysis employs analogous constructs within the non-Archimedean p-adic field, leading to key differences in convergence and analytic continuation principles. Despite these differences, both theories share common goals in understanding holomorphic functions, with notable results like the p-adic analog of Liouville's theorem highlighting their structural similarities and unique behaviors.
Open Problems and Research Directions
Complex analysis explores properties of holomorphic functions over the complex numbers, with open problems including the distribution of zeros of zeta functions and value distribution theory. P-adic analysis studies functions defined over p-adic number fields, where ongoing research investigates the extension of classical complex analytic results, p-adic differential equations, and the development of p-adic Hodge theory. Current directions emphasize bridging these fields through non-archimedean geometry and applications in number theory, such as understanding p-adic L-functions and their analytic continuation.
Conclusion: Bridging Complex and P-adic Worlds
Complex analysis and p-adic analysis both explore functions and continuity but operate within fundamentally different number systems: the complex numbers involve Archimedean absolute values, while p-adic analysis is rooted in non-Archimedean valuation. Bridging these domains reveals deep connections, such as through the study of zeta functions and arithmetic geometry, which utilize tools from both frameworks to understand number-theoretic phenomena. This interplay enriches mathematical insights by combining analytic techniques to address problems inaccessible within a single system alone.
Complex analysis Infographic
 libterm.com
libterm.com