Homomorphism is a fundamental concept in algebra that describes a structure-preserving map between two algebraic systems, such as groups, rings, or vector spaces. This mapping ensures that operations performed within one system correspond directly to operations in the other, maintaining the integrity of algebraic properties. Explore the rest of the article to understand how homomorphisms apply to various mathematical structures and why they are essential in abstract algebra.
Table of Comparison
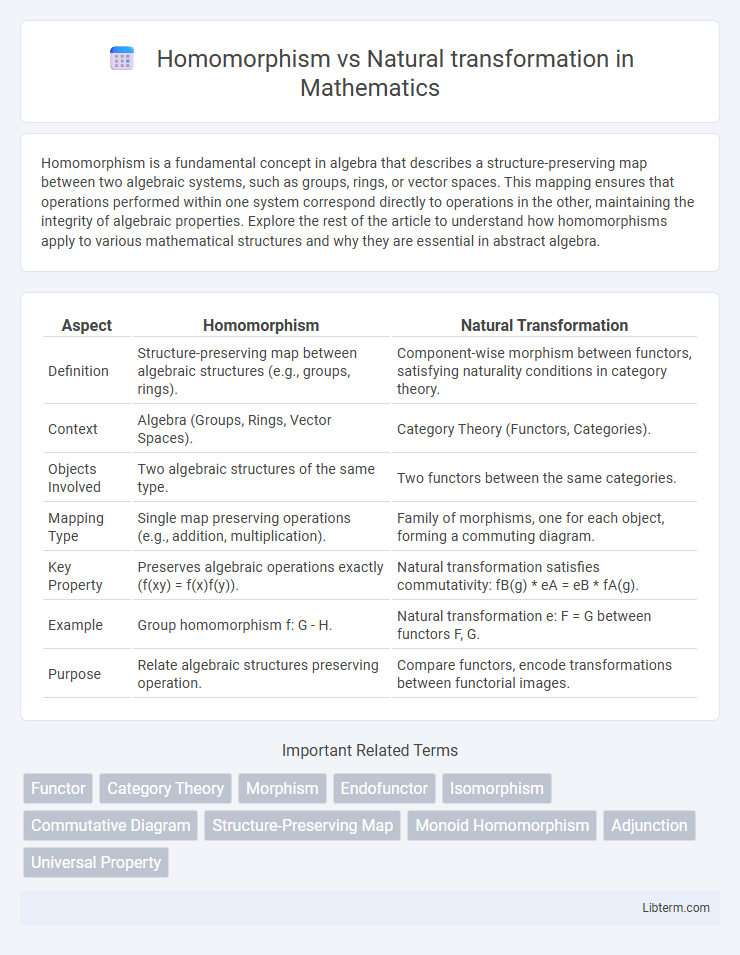
| Aspect | Homomorphism | Natural Transformation |
|---|---|---|
| Definition | Structure-preserving map between algebraic structures (e.g., groups, rings). | Component-wise morphism between functors, satisfying naturality conditions in category theory. |
| Context | Algebra (Groups, Rings, Vector Spaces). | Category Theory (Functors, Categories). |
| Objects Involved | Two algebraic structures of the same type. | Two functors between the same categories. |
| Mapping Type | Single map preserving operations (e.g., addition, multiplication). | Family of morphisms, one for each object, forming a commuting diagram. |
| Key Property | Preserves algebraic operations exactly (f(xy) = f(x)f(y)). | Natural transformation satisfies commutativity: fB(g) * eA = eB * fA(g). |
| Example | Group homomorphism f: G - H. | Natural transformation e: F = G between functors F, G. |
| Purpose | Relate algebraic structures preserving operation. | Compare functors, encode transformations between functorial images. |
Introduction to Homomorphism and Natural Transformation
Homomorphisms are structure-preserving maps between algebraic structures such as groups, rings, or vector spaces, ensuring operations within these structures are consistently maintained. Natural transformations, fundamental in category theory, provide a way to transform one functor into another while respecting the internal structure of categories involved. Both concepts capture essential notions of morphisms, but homomorphisms operate within algebraic frameworks, whereas natural transformations function at the level of functors between categories.
Fundamental Concepts in Category Theory
Homomorphisms are structure-preserving maps between algebraic objects such as groups, rings, or vector spaces, ensuring operations remain consistent within the target structure. Natural transformations provide a way to compare functors, mapping between categories by assigning morphisms that satisfy the naturality condition, reflecting categorical coherence. Both concepts are central in category theory, with homomorphisms highlighting object-level morphisms and natural transformations emphasizing morphisms between functors, fundamental for understanding categorical structures and their interrelations.
Definition of Homomorphism
A homomorphism is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defining those structures. It ensures that the image of the operation applied to elements in the domain equals the operation applied to their images in the codomain, maintaining the algebraic relationships intact. Compared to a natural transformation, which involves morphisms between functors in category theory, a homomorphism directly relates elements within algebraic objects rather than mapping between functorial contexts.
Definition of Natural Transformation
A natural transformation is a morphism between two functors that preserves the internal structure and commutes with all the morphisms in the source category, providing a way to compare functors categorically. While a homomorphism is a structure-preserving map between algebraic structures like groups or rings, a natural transformation operates at the level of functors, ensuring coherence between their actions on objects and morphisms. It consists of a family of morphisms indexed by objects, satisfying the naturality condition essential for categorical consistency.
Structural Differences Between Homomorphism and Natural Transformation
Homomorphisms are structure-preserving maps between algebraic objects like groups or rings, maintaining operations such as addition or multiplication within a fixed category. Natural transformations, in contrast, exist between functors and provide a systematic way to transform one functor into another while respecting the internal structure of categories and objects. The key structural difference lies in homomorphisms acting on elements within a single category, whereas natural transformations operate at the level of morphisms between functors, relating entire category mappings.
Examples of Homomorphism in Mathematics
Homomorphisms in mathematics are structure-preserving maps between algebraic objects such as groups, rings, or vector spaces, exemplified by a group homomorphism f: G - H that satisfies f(xy) = f(x)f(y) for all x, y in G. For instance, the exponential map from the additive group of real numbers (R, +) to the multiplicative group of positive real numbers (R^+, x), defined by f(x) = e^x, is a classic example of a group homomorphism. Unlike natural transformations, which are mappings between functors preserving categorical structure across different categories, homomorphisms focus on preserving algebraic operations within a single category.
Examples of Natural Transformation in Category Theory
Natural transformations provide a concrete way to compare functors by assigning a morphism to each object while preserving structural consistency across categories. For example, consider the natural transformation between the identity functor and the double dual functor on the category of vector spaces, where each vector space V maps to the canonical embedding of V into its double dual V. Another classic example is the natural transformation from the free group functor to the underlying set functor, illustrating how natural transformations capture systematic relationships beyond mere homomorphisms.
Applications in Algebra and Topology
Homomorphisms serve as fundamental tools in algebra for preserving structure when mapping between groups, rings, or vector spaces, enabling the classification and analysis of algebraic objects through kernel and image properties. Natural transformations provide a way to compare functors, facilitating the study of relationships between different categories, especially in topology where they are instrumental in defining homology and cohomology theories. Applications in algebra include the use of homomorphisms in group theory and module theory, while natural transformations underpin the structural understanding of continuous mappings and fibrations in algebraic topology.
Comparative Analysis: Homomorphism vs Natural Transformation
Homomorphisms are structure-preserving maps between algebraic structures like groups or rings, ensuring that operations remain consistent under the mapping. Natural transformations provide a systematic way to compare functors between categories, offering a higher-level correspondence that respects the composition and identities within those categories. Unlike homomorphisms that operate on individual algebraic objects, natural transformations function between entire functors, enabling comparisons across categories rather than just within a single algebraic structure.
Conclusion and Key Takeaways
Homomorphisms are structure-preserving maps between algebraic structures, essential for understanding internal symmetries and operations within a single category. Natural transformations provide a way to compare functors, highlighting relationships between different categories through component-wise morphisms that respect the categorical framework. The key takeaway is that homomorphisms operate within structures, while natural transformations operate between functors, making each fundamental in category theory but serving distinct conceptual roles.
Homomorphism Infographic
 libterm.com
libterm.com