Multiple value concepts enhance decision-making by integrating diverse perspectives and data sources, leading to more comprehensive and balanced outcomes. These approaches drive innovation and adaptability in complex environments by acknowledging the importance of varied stakeholder needs and interests. Explore the rest of the article to discover how you can leverage multiple value strategies for improved results.
Table of Comparison
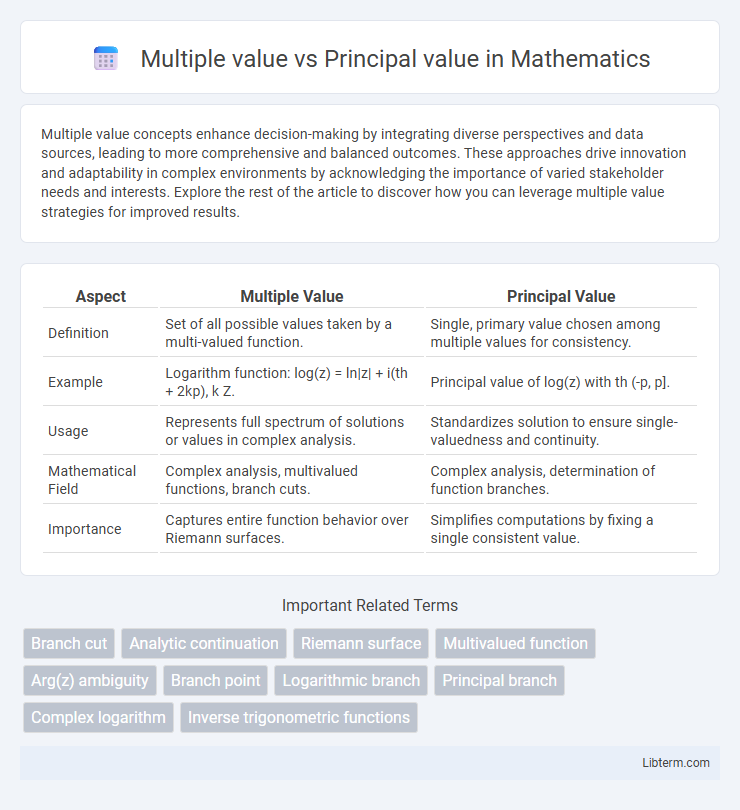
| Aspect | Multiple Value | Principal Value |
|---|---|---|
| Definition | Set of all possible values taken by a multi-valued function. | Single, primary value chosen among multiple values for consistency. |
| Example | Logarithm function: log(z) = ln|z| + i(th + 2kp), k Z. | Principal value of log(z) with th (-p, p]. |
| Usage | Represents full spectrum of solutions or values in complex analysis. | Standardizes solution to ensure single-valuedness and continuity. |
| Mathematical Field | Complex analysis, multivalued functions, branch cuts. | Complex analysis, determination of function branches. |
| Importance | Captures entire function behavior over Riemann surfaces. | Simplifies computations by fixing a single consistent value. |
Understanding Multiple Value and Principal Value
Multiple value refers to the set of all possible outputs of a complex function, such as the multiple values of the complex logarithm resulting from its periodicity. Principal value is a single, specifically chosen value from this set that serves as a standard or reference, for example, the principal branch of the logarithm defined with an argument between -p and p. Understanding the distinction between multiple values and principal value is crucial in complex analysis to correctly interpret multi-valued functions and ensure consistency in calculations.
Definition of Multiple Value
Multiple value refers to the set of all possible outputs or results obtained from a complex function or operation, often involving multi-valued functions such as the complex logarithm or square root. In contrast, the principal value is a specific branch or single value selected from the multiple possible values to maintain consistency and avoid ambiguity. Understanding multiple values is crucial in complex analysis for accurately describing functions that inherently produce more than one result.
Definition of Principal Value
Principal value refers to the unique value assigned to a function with multiple values, such as a complex logarithm or inverse trigonometric function, by restricting its domain and range to ensure a single, consistent output. Multiple values arise naturally in these functions due to periodicity or branch cuts, leading to various possible outputs. The principal value is critical in complex analysis for providing a standard solution that simplifies calculations and interpretation.
Key Differences Between Multiple Value and Principal Value
Multiple value refers to all possible values a function can output for a given input in complex analysis, while principal value specifically denotes the primary or main value selected from these multiple possibilities. The principal value is often used to define a single-valued function from a multi-valued one by restricting the domain or range, especially in functions like logarithms and inverse trigonometric functions. Key differences include multiple value representing the full set of solutions, whereas principal value is a conventionally chosen single value for consistent computation and interpretation.
Mathematical Contexts: Where Each Applies
Multiple value solutions commonly appear in complex analysis, especially with multi-valued functions like the complex logarithm or inverse trigonometric functions, where branches of values exist due to periodicity or multi-branch nature. Principal value refers to selecting a specific single value from these multiple values, often by defining a branch cut to maintain continuity and consistency in complex integrals or functions. In integral calculus and Hilbert transforms, principal value integrals handle singularities by symmetrically limiting the integral, while multiple values arise naturally in solving differential equations or complex functions with ambiguous outputs.
Examples Illustrating Multiple Values
Complex functions like the logarithm exhibit multiple values due to periodicity, for example, the complex logarithm \( \log z = \ln|z| + i(\arg z + 2\pi k) \) where \( k \) is any integer, leading to infinitely many values. Another example is the complex square root function, where \( \sqrt{z} \) has two values for each nonzero \( z \), typically represented as \( r^{1/2} e^{i\theta/2} \) and \( -r^{1/2} e^{i\theta/2} \). These examples illustrate how multiple values arise from branch cuts and the multivalued nature of inverse functions in the complex plane, contrasting with the principal value which selects a single, consistent branch.
Examples Illustrating Principal Values
Principal value refers to the single, specific value assigned within a defined range, such as the principal branch of a complex logarithm or the principal angle between -p and p in trigonometry. For example, the principal value of the inverse tangent function, arctan(x), lies between -p/2 and p/2, providing a unique angle despite multiple possible coterminal angles. Similarly, the principal value of the complex logarithm Log(z) is typically taken with the argument (angle) restricted to (-p, p], ensuring a consistent and single-valued output compared to multiple possible logarithmic values.
Importance in Complex Analysis
Multiple values arise in complex analysis when functions like the complex logarithm or complex roots assign several valid outputs to a single input, reflecting the function's multi-valued nature on the complex plane. The principal value selects a specific branch of these multiple values, ensuring a single, consistent output essential for defining branches of multi-valued functions and performing integrals. Understanding the distinction and proper usage of principal values is crucial for solving complex integrals, evaluating contour integrals, and applying branch cuts in analytic continuation.
Common Misconceptions and Pitfalls
Multiple value solutions often cause confusion as they represent all possible angles in trigonometric equations, whereas principal value refers to the single, primary angle within a specified range. A common misconception is treating the principal value as the only valid solution, ignoring the infinite set of solutions that arise due to periodicity. Pitfalls include incorrect problem-solving by overlooking multiple values, leading to incomplete or erroneous results in trigonometry and inverse function evaluations.
Practical Applications in Science and Engineering
Multiple values in complex analysis arise when solving equations like roots and logarithms, providing comprehensive solutions essential for electronic circuit design and control systems. Principal value selects a single, well-defined branch from these multiple values, facilitating practical computation and interpretation in signal processing and fluid dynamics. Engineers rely on principal values to maintain consistency and stability in numerical simulations and analytical modeling.
Multiple value Infographic
 libterm.com
libterm.com