Coanalytic sets, also known as P11 sets, are complements of analytic sets within descriptive set theory, playing a crucial role in the hierarchy of definable sets in Polish spaces. These sets are intricate and often arise in contexts involving projective sets, showing properties vital for understanding complexity beyond Borel sets. Explore the rest of this article to deepen your comprehension of coanalytic sets and their applications in advanced mathematical theory.
Table of Comparison
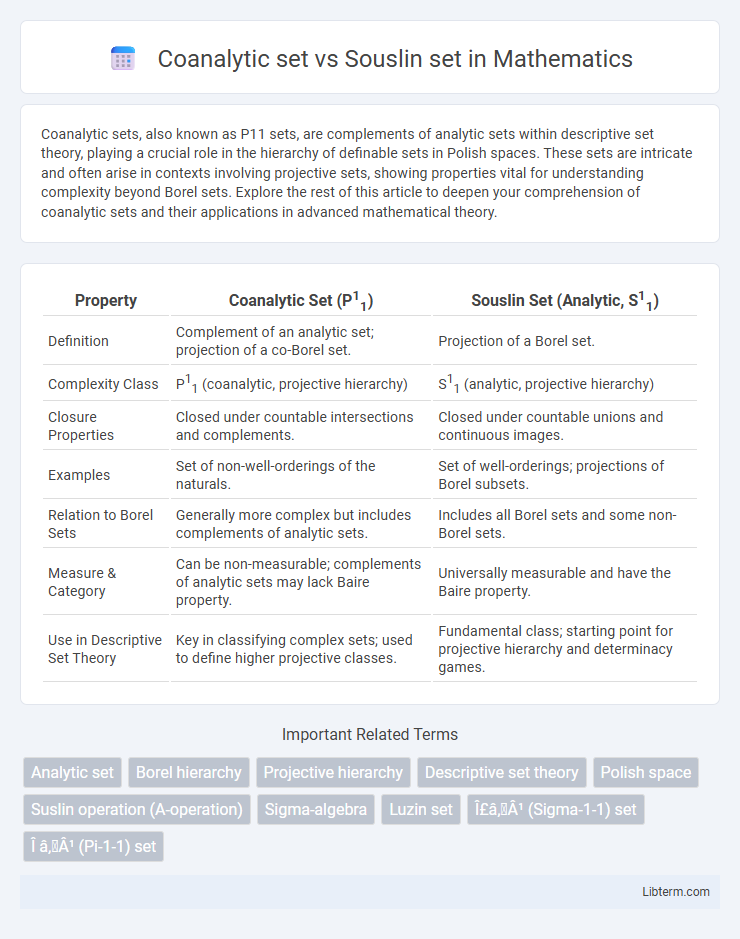
| Property | Coanalytic Set (P11) | Souslin Set (Analytic, S11) |
|---|---|---|
| Definition | Complement of an analytic set; projection of a co-Borel set. | Projection of a Borel set. |
| Complexity Class | P11 (coanalytic, projective hierarchy) | S11 (analytic, projective hierarchy) |
| Closure Properties | Closed under countable intersections and complements. | Closed under countable unions and continuous images. |
| Examples | Set of non-well-orderings of the naturals. | Set of well-orderings; projections of Borel subsets. |
| Relation to Borel Sets | Generally more complex but includes complements of analytic sets. | Includes all Borel sets and some non-Borel sets. |
| Measure & Category | Can be non-measurable; complements of analytic sets may lack Baire property. | Universally measurable and have the Baire property. |
| Use in Descriptive Set Theory | Key in classifying complex sets; used to define higher projective classes. | Fundamental class; starting point for projective hierarchy and determinacy games. |
Introduction to Coanalytic and Souslin Sets
Coanalytic sets, also known as P11 sets, are complements of analytic (S11) sets in descriptive set theory and play a crucial role in the projective hierarchy by representing complex definable sets beyond Borel sets. Souslin sets, synonymous with analytic sets, are constructed through continuous images of Borel sets and provide a foundational class in analyzing the complexities of real-valued functions and Polish spaces. Understanding the distinction between coanalytic and Souslin sets is essential for exploring measurability, determinacy, and classification problems in advanced mathematical logic.
Defining Coanalytic Sets: Key Properties
Coanalytic sets, also known as P11 sets, are complements of analytic (S11) sets and are definable by universal quantification over Borel sets in descriptive set theory. These sets exhibit closure under countable intersections and continuous preimages but are not necessarily Borel, reflecting their position in the projective hierarchy. Key properties include their role in characterizing determinacy results and their nontrivial projective complexity compared to Souslin sets, which are analytic and obtained as continuous images of Borel sets.
Understanding Souslin Sets in Descriptive Set Theory
Souslin sets, also known as analytic sets, are projections of Borel sets in descriptive set theory, characterized by their definability through continuous images of Polish spaces. Coanalytic sets, or complements of analytic sets, represent a broader complexity class, often studied through their descriptive and topological properties. Understanding Souslin sets involves analyzing their position within the projective hierarchy, where they serve as foundational examples of definable non-Borel sets with significant applications in measure theory and effective descriptive set theory.
Historical Background: Origins of Coanalytic and Souslin Sets
Coanalytic sets, also known as P11 sets, were first studied in the 20th century as a key class in descriptive set theory, extending the Borel hierarchy beyond analytic sets. Souslin sets originated from Mikhail Souslin's work in 1917, who identified these sets while investigating the properties of analytic sets and counterexamples to the completeness of Borel sets. The development of coanalytic and Souslin sets laid foundational groundwork for modern descriptive set theory, influencing the understanding of projective hierarchies and measurable selection theorems.
Relationship Between Coanalytic Sets and Souslin Sets
Coanalytic sets, also known as P11 sets, are complements of analytic (S11) sets in descriptive set theory, while Souslin sets refer to analytic sets characterized by a tree-like representation known as the Souslin operation. The relationship between coanalytic sets and Souslin sets is that every analytic set is a Souslin set, and coanalytic sets are complements of these Souslin sets in Polish spaces. This duality means coanalytic sets frequently arise as complements of Souslin sets, highlighting a fundamental interplay in the projective hierarchy between analytic (Souslin) and coanalytic classes.
Important Theorems Involving Coanalytic and Souslin Sets
Important theorems involving coanalytic and Souslin sets include the Lusin separation theorem, which states that any two disjoint coanalytic sets can be separated by a Borel set, highlighting the structural clarity of these classes. The Souslin operation characterizes analytic sets and shows that Souslin sets can be represented as continuous images of Polish spaces, linking topology and descriptive set theory. Moreover, the Luzin hierarchy demonstrates that coanalytic sets are complements of analytic sets, establishing a duality crucial for measure and category arguments in Polish spaces.
Differences Between Coanalytic Sets and Souslin Sets
Coanalytic sets, also known as P11 sets, are complements of analytic sets and are characterized by their definability in descriptive set theory, whereas Souslin sets are synonymous with analytic sets defined by continuous images of Borel sets. The primary difference lies in their construction: coanalytic sets arise as complements, emphasizing their position in the projective hierarchy, while Souslin sets are typically generated through projection operations from Borel sets. This distinction impacts their topological and measure-theoretic properties, with Souslin sets being universally measurable and coanalytic sets potentially more complex and less regular.
Examples of Coanalytic and Souslin Sets
Coanalytic sets, also known as \(\mathbf{\Pi^1_1}\) sets, include classic examples such as the set of all well-orderings of the natural numbers and the set of all real numbers coding non-well-founded trees. Souslin sets, which are projections of Borel sets, notably contain all analytic sets (\(\mathbf{\Sigma^1_1}\)) and can be exemplified by the projection of the set of infinite branches through a closed tree on \(\mathbb{N}\times \mathbb{N}\). While every analytic set is Souslin, not all Souslin sets are Borel, and coanalytic sets often arise as complements of analytic sets, highlighting their distinct definability in descriptive set theory.
Applications in Modern Mathematics
Coanalytic sets, defined as complements of analytic sets in descriptive set theory, play a crucial role in fields like recursion theory and effective descriptive set theory by characterizing complex definability and computability properties. Souslin sets, also known as analytic sets, are vital in measure theory, topology, and functional analysis due to their closure properties and ability to represent complex Borel hierarchies, enabling advanced classification of measurable and topological spaces. Applications of these sets extend to real analysis, probability theory, and dynamical systems, where they facilitate the study of definable sets and functions, impacting problems involving measurability, classification, and complexity.
Open Problems and Future Directions in Set Theory
Coanalytic sets, defined as complements of analytic sets, present open problems related to their descriptive complexity and structural characteristics, particularly in relation to projective determinacy and definability hierarchies. Souslin sets, characterized by their construction through Souslin schemes and linked to classical descriptive set theory, raise questions about their boundary with Borel and analytic classes, and the potential for new hierarchies beyond established frameworks. Future directions in set theory explore the interactions between large cardinal axioms and the classification of these sets, aiming to resolve unresolved problems regarding uniformization, regularity properties, and finer stratifications within the projective hierarchy.
Coanalytic set Infographic
 libterm.com
libterm.com