Consistency plays a crucial role in achieving long-term success by establishing reliable habits and building trust. Maintaining a steady routine enhances productivity and ensures continual progress toward your goals. Explore the rest of this article to learn effective strategies for staying consistent in every aspect of your life.
Table of Comparison
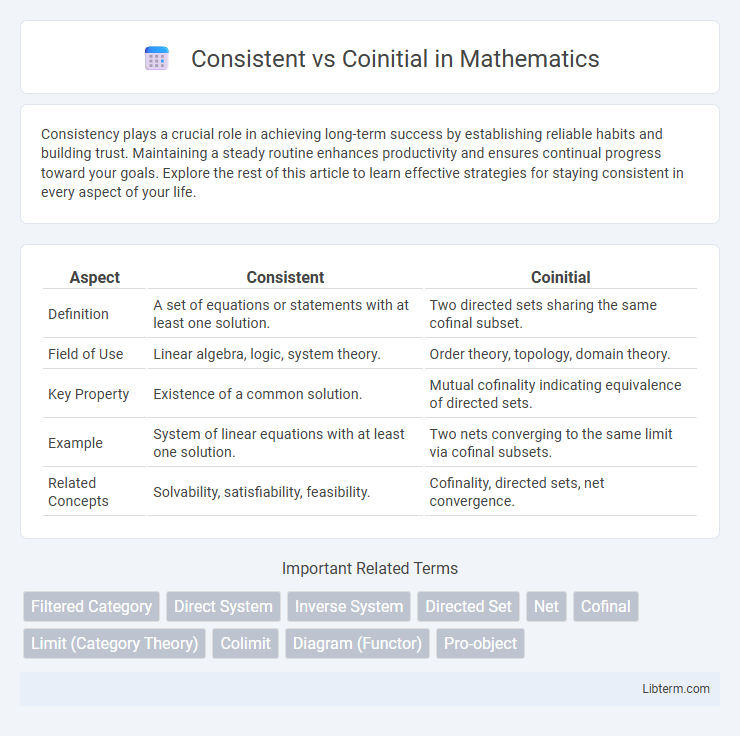
| Aspect | Consistent | Coinitial |
|---|---|---|
| Definition | A set of equations or statements with at least one solution. | Two directed sets sharing the same cofinal subset. |
| Field of Use | Linear algebra, logic, system theory. | Order theory, topology, domain theory. |
| Key Property | Existence of a common solution. | Mutual cofinality indicating equivalence of directed sets. |
| Example | System of linear equations with at least one solution. | Two nets converging to the same limit via cofinal subsets. |
| Related Concepts | Solvability, satisfiability, feasibility. | Cofinality, directed sets, net convergence. |
Introduction to Consistent and Coinitial
Consistent and coinitial are key concepts in order theory and lattice theory, describing relationships between elements in partially ordered sets. A consistent set consists of elements that can coexist without contradiction, ensuring that no element conflicts with another within the set. Coinitiality refers to a subset where every element of the larger set has a lower bound within the subset, effectively capturing the notion of a set being "initial" or "starting point" in terms of order relation.
Defining Consistency in Mathematical Structures
Consistency in mathematical structures refers to the absence of contradictions within a set of axioms or propositions, ensuring that no statement and its negation can both be derived. Consistent systems permit the development of theorems and logical deductions that are reliable and verifiable within that framework. This foundational property distinguishes consistent theories from inconsistent or contradictory ones, maintaining the integrity of mathematical logic and reasoning.
Understanding Coinitiality: A Semantic Perspective
Coinitiality refers to two or more sets starting at the same point in a partially ordered structure, often studied within the context of order theory and lattice theory. Understanding coinitiality involves analyzing how these sets share a common lower bound, which influences properties like completeness and convergence in semantic domains. This concept contrasts with consistency, which concerns the compatibility or non-contradiction of elements rather than their positional relationships within an ordered set.
Key Differences Between Consistent and Coinitial
Consistent filters ensure that the order of elements is preserved when refining data sets, maintaining semantic integrity across operations. Coinitial filters, by contrast, focus on the initial segments that overlap between sets, emphasizing common starting points rather than full order preservation. The key difference lies in consistent filters prioritizing order consistency, while coinitial filters prioritize shared initial elements for data comparison or merging.
Applications of Consistent Sets in Logic
Consistent sets in logic are crucial for ensuring that no contradictions arise within a given theory, enabling reliable deduction and inference in formal systems. Applications of consistent sets include the construction of models in model theory, where they help confirm the satisfiability of a set of formulas and support completeness theorems. These sets underpin automated theorem proving by guaranteeing that derived conclusions maintain logical coherence throughout computational processes.
Coinitial Sets in Order Theory and Their Importance
Coinitial sets in order theory are subsets of a partially ordered set where every element in the larger set is greater than or equal to some element in the coinitial set, ensuring coverage from below. These sets are crucial for analyzing lower bounds and constructing infima, playing a vital role in completeness properties of ordered structures. Unlike consistent sets that maintain logical coherence, coinitial sets provide foundational elements that anchor the structure's ordering hierarchy.
Real-World Examples of Consistent and Coinitial Concepts
Consistent concepts often appear in software versioning where backward compatibility ensures stable user experience, such as maintaining API functionality across updates. Coinitial examples emerge in linguistics when different expressions share identical starting points in semantic structure despite divergent meanings, like synonyms initiating similar conceptual frameworks. In physics, consistent temporal sequences of events contrast with coinitial events occurring simultaneously yet diverging in outcome, illustrating the practical distinction between these concepts.
Why Distinguishing Between Consistent and Coinitial Matters
Distinguishing between consistent and coinitial properties is crucial in formal logic and model theory for accurately analyzing the structure of theories and their extensions. Consistent sets represent collections of formulas that can coexist without contradiction, ensuring the existence of at least one model, while coinitial sets relate to minimal elements in partially ordered sets and influence the evaluation of initial segments in ordered structures. Understanding these differences impacts the development of proofs, the classification of theories, and the assessment of logical entailment, thereby enhancing the precision of theoretical foundations and applications in computational logic.
Common Misconceptions About Consistent vs Coinitial
Common misconceptions about consistent vs coinitial terms often arise from confusing their distinct mathematical properties; consistent refers to conditions that do not contradict each other, while coinitial relates to elements sharing the same initial point in an ordered structure. Many incorrectly assume that coinitial implies consistency or vice versa, overlooking that consistency addresses logical compatibility and coinitiality pertains to positional alignment within sets or sequences. Clarifying these differences enhances understanding in fields such as topology, algebra, and order theory, where precise definitions impact theorem formulation and proofs.
Summary: Choosing the Right Concept for Your Framework
Consistent frameworks prioritize maintaining uniformity in data or processes, ensuring reliability and predictability across different operations. Coinitial frameworks focus on aligning starting points or initial conditions to facilitate comparability and coordination in complex systems. Selecting the appropriate concept depends on whether uniformity or initial alignment better supports your specific application's goals and operational context.
Consistent Infographic
 libterm.com
libterm.com