Preordering ensures you secure the latest products before they officially launch, avoiding stock shortages and price hikes. It offers the advantage of exclusive bonuses and early access that are often unavailable after the release date. Discover how preordering can benefit your shopping experience by reading the rest of this article.
Table of Comparison
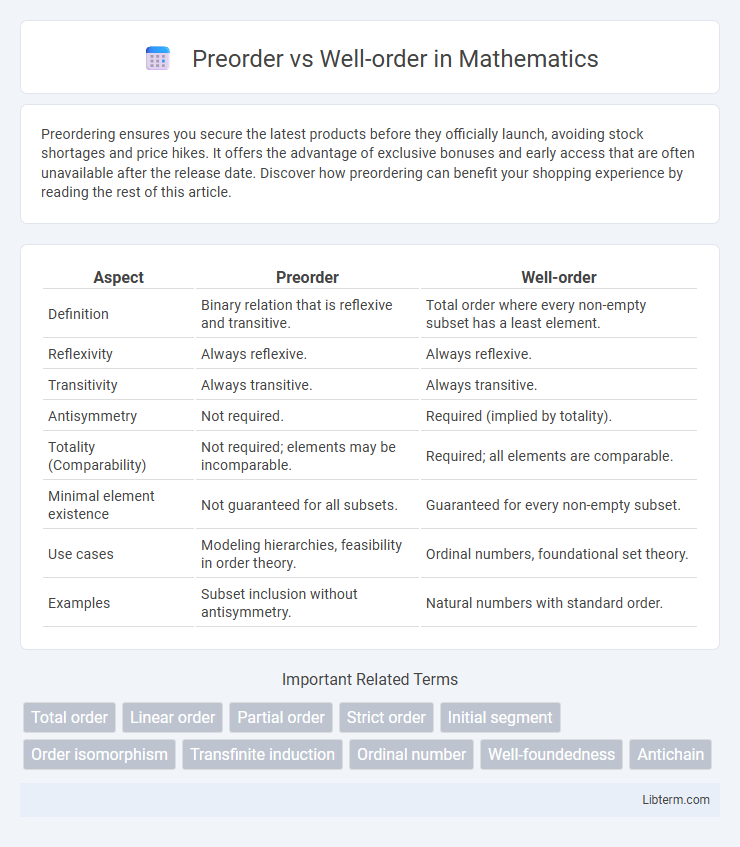
| Aspect | Preorder | Well-order |
|---|---|---|
| Definition | Binary relation that is reflexive and transitive. | Total order where every non-empty subset has a least element. |
| Reflexivity | Always reflexive. | Always reflexive. |
| Transitivity | Always transitive. | Always transitive. |
| Antisymmetry | Not required. | Required (implied by totality). |
| Totality (Comparability) | Not required; elements may be incomparable. | Required; all elements are comparable. |
| Minimal element existence | Not guaranteed for all subsets. | Guaranteed for every non-empty subset. |
| Use cases | Modeling hierarchies, feasibility in order theory. | Ordinal numbers, foundational set theory. |
| Examples | Subset inclusion without antisymmetry. | Natural numbers with standard order. |
Introduction to Order Relations
Order relations classify sets based on how elements compare, with preorder relations allowing reflexivity and transitivity but not requiring antisymmetry, forming a broader category than well-orders. Well-orders impose stricter conditions by being total, well-founded, and antisymmetric, ensuring every non-empty subset has a least element. Understanding preorder versus well-order distinctions is crucial for analyzing hierarchical structures and organizing data in mathematics and computer science.
Defining Preorder Structures
Preorder structures are binary relations that are reflexive and transitive, allowing elements to be compared in a way that may not be antisymmetric, distinguishing them from partial orders. In a preorder, elements can be related in cycles or equivalently without implying strict order, making it a more general framework. Well-order structures extend partial orders by requiring every non-empty subset to have a least element, a property not guaranteed in preorders.
Understanding Well-order Concepts
Well-ordering is a strict total order on a set where every non-empty subset has a least element, distinguishing it from a preorder which may lack such minimal elements. This property ensures that induction principles apply, enabling proofs and constructions based on the smallest element in any subset. Understanding well-orders is fundamental in set theory and ordinal analysis, highlighting their role in defining transfinite sequences and hierarchies.
Key Differences Between Preorder and Well-order
A preorder is a binary relation that is reflexive and transitive, allowing for elements to be incomparable, whereas a well-order is a total order that is also well-founded, ensuring every non-empty subset has a least element. Preorders do not require antisymmetry, so distinct elements can be mutually related, but well-orders are antisymmetric, making orderings strictly linear. Well-orders facilitate induction and recursion principles due to their minimal element property, while preorders lack this guarantee, limiting their use in constructive arguments.
Examples of Preorder in Mathematics
A preorder in mathematics is a binary relation that is reflexive and transitive but not necessarily antisymmetric, making it more general than a partial order or well-order. Examples of preorders include the reachability relation in directed graphs, where one vertex can reach another through a sequence of edges, and the divisibility relation on natural numbers without enforcing antisymmetry on equivalence classes. Another example is the set of words ordered by the prefix relation, which is reflexive and transitive but does not establish a total or well-ordering.
Examples of Well-order in Mathematics
Well-orders appear prominently in set theory, where the set of all ordinal numbers exemplifies a fundamental well-ordered structure, ensuring every non-empty subset has a least element. The natural numbers \(\mathbb{N}\) with their usual ordering form a canonical example of a well-ordered set, essential for defining induction and recursion. Beyond \(\mathbb{N}\), the lexicographic ordering on finite sequences of natural numbers also establishes a well-order, utilized in proofs involving transfinite induction.
Properties of Preorders
Preorders are binary relations on a set that are reflexive and transitive, ensuring every element relates to itself and that the relation maintains consistency through chains of elements. Unlike partial orders, preorders do not require antisymmetry, allowing distinct elements to be mutually comparable. These properties enable preorders to generalize partial orders, serving as foundational structures in fields like category theory and computer science for modeling hierarchical or preference relations without strict ordering constraints.
Properties of Well-orders
Well-orders are total orders with the additional property that every non-empty subset has a least element, ensuring no infinite descending chains exist. This minimum element characteristic enables transfinite induction and recursion on ordinals, making well-orders foundational in set theory. Unlike preorders, well-orders guarantee antisymmetry and linearity, resulting in a strict hierarchical structure critical for ordinal classification.
Applications in Set Theory and Logic
Preorders, characterized by reflexivity and transitivity, are essential in computer science for modeling type hierarchies and ordinal analysis in set theory. Well-orders, which extend linear orders by requiring every non-empty subset to have a least element, underpin the definition of ordinals and enable transfinite induction, a cornerstone technique in proofs and model theory. Applications in logic leverage well-orders to establish consistency proofs and ordinal assignments, while preorders support reasoning about equivalence classes and partial information structures.
Summary: Choosing Between Preorder and Well-order
Preorders and well-orders differ primarily in their structural properties and applications: preorders allow reflexivity and transitivity without requiring antisymmetry, making them suitable for modeling scenarios with indistinct elements or equivalence classes. Well-orders are total orders with the added property that every non-empty subset has a least element, essential for inductive arguments and ordinal analysis. Choosing between preorder and well-order depends on whether the application demands strict hierarchy and minimal elements (well-order) or more flexible, possibly non-antisymmetric relations (preorder).
Preorder Infographic
 libterm.com
libterm.com