Preorder is a purchasing method allowing you to reserve a product before its official release, ensuring early access and guaranteed availability. This strategy benefits both consumers eager for the latest items and businesses managing demand forecasts effectively. Discover how preorder can enhance your shopping experience by exploring the full article.
Table of Comparison
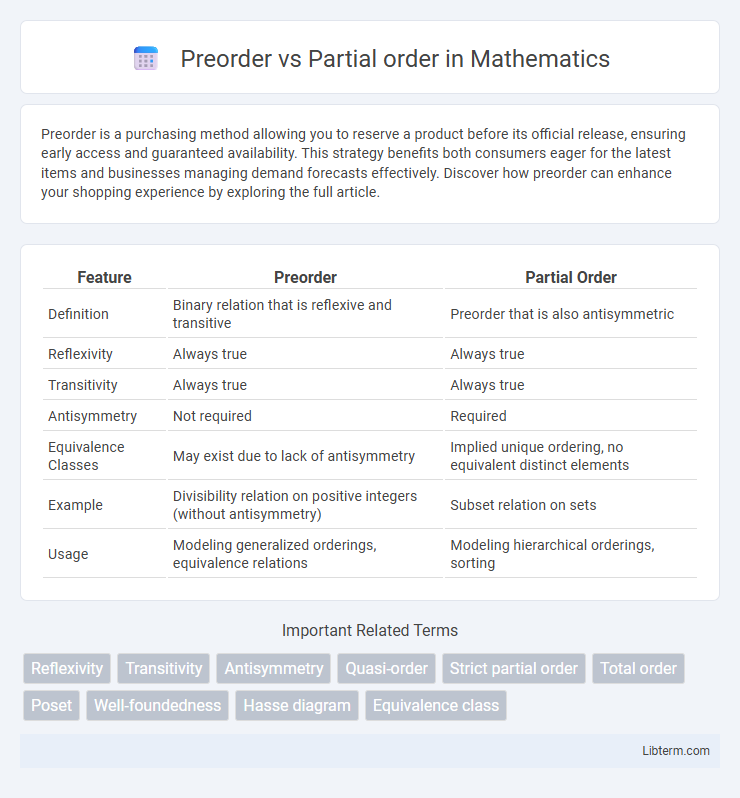
| Feature | Preorder | Partial Order |
|---|---|---|
| Definition | Binary relation that is reflexive and transitive | Preorder that is also antisymmetric |
| Reflexivity | Always true | Always true |
| Transitivity | Always true | Always true |
| Antisymmetry | Not required | Required |
| Equivalence Classes | May exist due to lack of antisymmetry | Implied unique ordering, no equivalent distinct elements |
| Example | Divisibility relation on positive integers (without antisymmetry) | Subset relation on sets |
| Usage | Modeling generalized orderings, equivalence relations | Modeling hierarchical orderings, sorting |
Introduction to Preorder and Partial Order
Preorders and partial orders are mathematical structures used to describe relationships between elements based on a binary relation. A preorder is a relation that is reflexive and transitive, allowing for elements to be comparable in a non-strict hierarchy, but not necessarily antisymmetric. Partial orders extend preorders by adding the antisymmetry property, which ensures that no two distinct elements are mutually related, providing a stricter framework for ordering elements without requiring total comparability.
Defining Preorder: Key Characteristics
A preorder is a binary relation on a set that is reflexive and transitive, meaning every element is related to itself, and if an element is related to a second element, which in turn is related to a third, then the first is related to the third. Unlike a partial order, a preorder does not require antisymmetry, so two distinct elements can be mutually related. This relaxation allows preorders to represent more general ordering structures where equivalences or cycles may exist.
Understanding Partial Order: Main Features
Partial orders are binary relations characterized by reflexivity, antisymmetry, and transitivity, ensuring elements can be compared without requiring all pairs to be related. Unlike preorders, partial orders prohibit cycles where distinct elements relate bidirectionally, providing a structured hierarchy ideal for sorting and hierarchy modeling. This distinction allows partial orders to represent well-defined partial hierarchies in data structures, posets, and lattice theory applications.
Mathematical Foundations of Preorder and Partial Order
A preorder on a set is a binary relation that is reflexive and transitive, allowing elements to be comparable in a non-antisymmetric way, meaning distinct elements can relate mutually. Partial orders refine preorders by enforcing antisymmetry, ensuring if two elements relate to each other, they must be identical, which structures the set into a hierarchy without cycles. Both concepts underpin order theory in mathematics, with partial orders forming posets fundamental to lattice theory, while preorders accommodate more general relational frameworks.
Symmetry, Reflexivity, and Transitivity: A Comparison
Preorders and partial orders both exhibit reflexivity and transitivity, ensuring every element relates to itself and that the relation is consistent across elements. Partial orders differ by being antisymmetric, prohibiting two distinct elements from mutually relating, whereas preorders allow symmetry without this restriction. This distinction means partial orders form a stricter hierarchy, while preorders accommodate equivalence classes through symmetric relations.
Visual Representation: Hasse Diagrams and Beyond
Preorder relations, characterized by reflexivity and transitivity, are visually represented by directed graphs that allow cycles and self-loops, whereas partial orders--being antisymmetric in addition--are depicted using Hasse diagrams, which eliminate reflexive loops and transitive edges for clarity. Hasse diagrams provide a simplified, transitive reduction form that highlights the immediate cover relations without showing implied connections, making partial order structures more intuitive and less cluttered. Beyond Hasse diagrams, alternative visualizations such as order dimension embeddings or lattice diagrams extend the analysis of partial orders by illustrating additional algebraic or topological properties unavailable in standard Hasse representations.
Real-World Applications: Where Preorder and Partial Order Apply
Preorders are commonly used in task scheduling and preference modeling where elements need to be compared with possible ties, enabling flexible ranking scenarios such as prioritizing customer demands or workflow steps. Partial orders find critical applications in dependency resolution systems like package managers, version control, and event scheduling, where a strict hierarchical structure without cycles ensures consistency and correctness. Both structures support hierarchical data organization, but partial orders enable defining clear precedence relations vital for critical path analysis and resource allocation.
Key Differences Between Preorder and Partial Order
Preorder relations allow reflexivity and transitivity but do not require antisymmetry, meaning distinct elements can be mutually related. Partial orders mandate antisymmetry along with reflexivity and transitivity, ensuring no two different elements are comparable in both directions. Consequently, all partial orders are preorders, but not all preorders qualify as partial orders due to the antisymmetry condition.
Choosing the Right Relation for Your Problem
Preorder relations allow reflexivity and transitivity without requiring antisymmetry, making them ideal for scenarios where elements can be equivalent but not strictly ordered, such as task scheduling with dependencies. Partial orders introduce antisymmetry, ensuring that no two distinct elements are mutually related, which fits hierarchical structures like file directory systems or version control histories. Choosing between preorder and partial order depends on whether equivalence classes need to be identified or a strict hierarchy must be maintained in the problem domain.
Conclusion: Preorder vs Partial Order Summarized
A preorder is a binary relation that is reflexive and transitive, allowing elements to be comparable without antisymmetry, meaning distinct elements can relate mutually. A partial order extends a preorder by adding antisymmetry, ensuring that if two elements relate bidirectionally, they must be identical, which provides a clearer hierarchical structure. Therefore, every partial order is a preorder, but not all preorders qualify as partial orders due to the absence of antisymmetry.
Preorder Infographic
 libterm.com
libterm.com