A non-measurable set is a collection of points that cannot be assigned a meaningful length, area, or volume using standard measures like the Lebesgue measure. These sets often arise in advanced mathematics, particularly in measure theory, challenging the intuitive notion of size and extent. Explore the rest of the article to understand how non-measurable sets impact mathematical analysis and your grasp of measurable spaces.
Table of Comparison
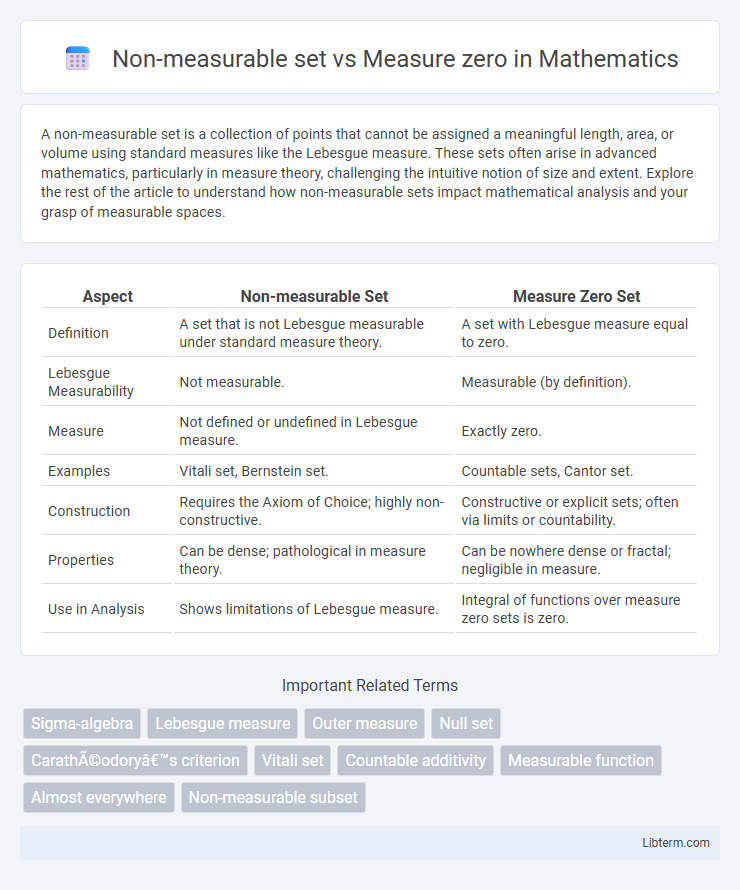
| Aspect | Non-measurable Set | Measure Zero Set |
|---|---|---|
| Definition | A set that is not Lebesgue measurable under standard measure theory. | A set with Lebesgue measure equal to zero. |
| Lebesgue Measurability | Not measurable. | Measurable (by definition). |
| Measure | Not defined or undefined in Lebesgue measure. | Exactly zero. |
| Examples | Vitali set, Bernstein set. | Countable sets, Cantor set. |
| Construction | Requires the Axiom of Choice; highly non-constructive. | Constructive or explicit sets; often via limits or countability. |
| Properties | Can be dense; pathological in measure theory. | Can be nowhere dense or fractal; negligible in measure. |
| Use in Analysis | Shows limitations of Lebesgue measure. | Integral of functions over measure zero sets is zero. |
Introduction to Measure Theory Concepts
Non-measurable sets arise in measure theory when certain subsets of a given space cannot be assigned a consistent measure, illustrating limitations of standard Lebesgue measure. Sets of measure zero, also known as null sets, have measure zero yet remain measurable and often serve as counterexamples or boundary cases within the theory. Understanding the distinction between non-measurable sets and measure zero sets is fundamental for grasping complexities in sigma algebras and measurable functions.
Defining Measure Zero Sets
Measure zero sets are subsets of a given measure space that can be covered by countably many intervals whose total length (measure) is arbitrarily small, effectively having zero "size" in terms of measure. Non-measurable sets, in contrast, cannot be assigned a consistent measure according to the rules of measure theory, often constructed using the axiom of choice. Defining measure zero sets involves verifying that for every e > 0, there exists a countable collection of intervals whose union contains the set and whose total measure sums to less than e.
Understanding Non-measurable Sets
Non-measurable sets arise in measure theory when certain subsets of real numbers cannot be assigned a consistent Lebesgue measure, contrasting with sets of measure zero which, despite having zero size in terms of measure, remain measurable. The Vitali set exemplifies a classic non-measurable set, constructed using the axiom of choice, demonstrating how translation-invariant measures fail to apply. Understanding non-measurable sets is crucial for grasping the limitations of Lebesgue measure and the necessity of careful set selection in analysis.
Criteria for Measurability
Non-measurable sets lack a well-defined outer measure consistent with the axioms of Lebesgue measure, failing Caratheodory's criterion which requires the measure of any set to be equal to the sum of the measures of its intersections with any partitioning set. Sets of measure zero satisfy this criterion trivially because their outer measure is zero, ensuring additivity and measurability. The primary difference lies in the Caratheodory condition: measure zero sets meet this criterion, while non-measurable sets do not, making the criterion essential for distinguishing measurable subsets in the Lebesgue measure framework.
Key Differences: Measure Zero vs Non-measurable Sets
Measure zero sets are subsets of a given space that can be covered by intervals with arbitrarily small total length, implying their Lebesgue measure is zero. Non-measurable sets, in contrast, lack a well-defined Lebesgue measure due to their construction, often relying on the axiom of choice, making them impossible to assign a consistent measure. The key difference lies in that measure zero sets are measurable with zero measure, whereas non-measurable sets defy any consistent measure assignment within Lebesgue theory.
Examples of Measure Zero Sets
Examples of measure zero sets include the Cantor set, the set of rational numbers within any interval, and finite or countable collections of points on the real line. These sets are negligible in terms of Lebesgue measure because their total length sums to zero despite containing infinitely many points. Non-measurable sets, such as the Vitali set, differ fundamentally as they cannot be assigned a consistent Lebesgue measure, contrasting measure zero sets that have well-defined zero measure.
Examples of Non-measurable Sets
Non-measurable sets arise in measure theory as subsets of real numbers that cannot be assigned a consistent Lebesgue measure, unlike measure-zero sets which have zero size in terms of Lebesgue measure. Classic examples of non-measurable sets include the Vitali set, constructed using the axiom of choice, which contains representatives from each equivalence class of real numbers modulo rational shifts and defies Lebesgue measurability. In contrast, measure-zero sets like the Cantor set are uncountably infinite yet still measurable, illustrating the fundamental difference between non-measurability and having zero measure.
Role of the Axiom of Choice
Non-measurable sets arise primarily due to the Axiom of Choice, which enables the selection of elements to construct sets without a well-defined Lebesgue measure. In contrast, measure zero sets have a definite measure of zero and can be constructed without invoking the Axiom of Choice. The Axiom of Choice is essential in demonstrating the existence of non-measurable sets like the Vitali set, highlighting its critical role in measure theory.
Implications in Real Analysis
Non-measurable sets demonstrate the limitations of Lebesgue measure by lacking a well-defined measure, highlighting challenges in extending countable additivity beyond measurable subsets of the real line. Sets of measure zero, although having no length, serve as critical examples where functions may be modified without affecting integrals or convergence properties in real analysis. Understanding the distinction clarifies the boundaries of measure theory, affecting the application of integration techniques, almost everywhere convergence, and differentiation theorems.
Applications and Importance in Mathematics
Non-measurable sets challenge the foundations of measure theory by lacking a well-defined Lebesgue measure, which complicates integration and probability calculations in real analysis. Sets of measure zero, however, are crucial in approximation, allowing mathematicians to ignore negligible subsets in limit processes and ensuring properties like almost everywhere convergence in functional analysis. These concepts underpin advanced fields such as ergodic theory, harmonic analysis, and fractal geometry, where distinguishing between measurable and non-measurable sets influences the formulation of theorems and practical problem-solving.
Non-measurable set Infographic
 libterm.com
libterm.com