An abelian category is a mathematical framework that generalizes the properties of abelian groups and modules, allowing for a structured study of homological algebra. This category features exact sequences, kernels, and cokernels, enabling the analysis of morphisms and objects with well-defined algebraic operations. Explore the full article to understand how abelian categories provide a foundation for advanced concepts in algebra and topology.
Table of Comparison
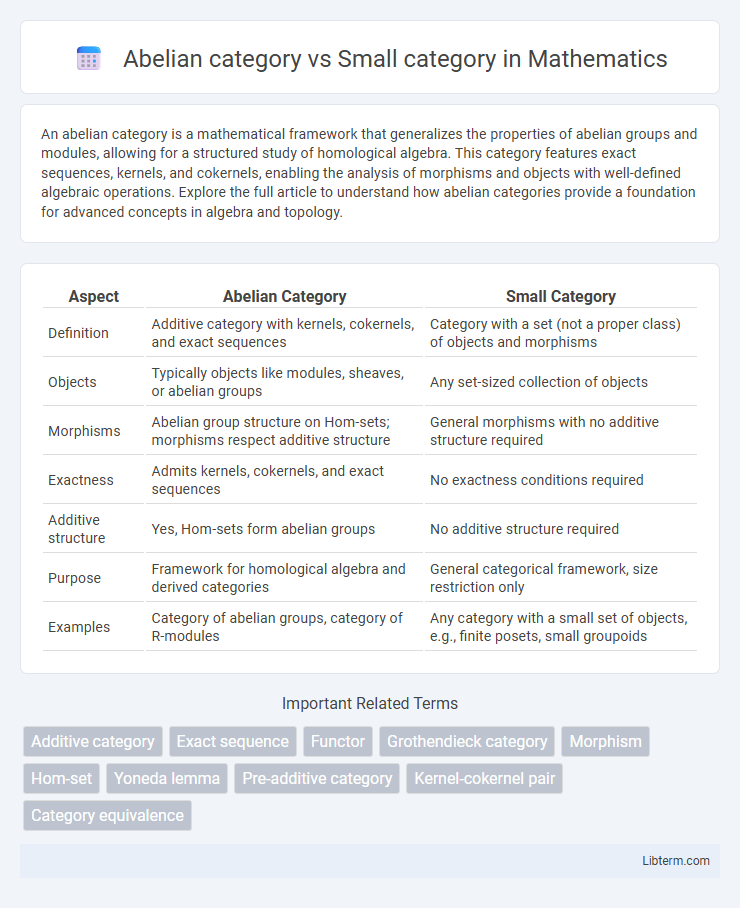
| Aspect | Abelian Category | Small Category |
|---|---|---|
| Definition | Additive category with kernels, cokernels, and exact sequences | Category with a set (not a proper class) of objects and morphisms |
| Objects | Typically objects like modules, sheaves, or abelian groups | Any set-sized collection of objects |
| Morphisms | Abelian group structure on Hom-sets; morphisms respect additive structure | General morphisms with no additive structure required |
| Exactness | Admits kernels, cokernels, and exact sequences | No exactness conditions required |
| Additive structure | Yes, Hom-sets form abelian groups | No additive structure required |
| Purpose | Framework for homological algebra and derived categories | General categorical framework, size restriction only |
| Examples | Category of abelian groups, category of R-modules | Any category with a small set of objects, e.g., finite posets, small groupoids |
Introduction to Abelian and Small Categories
Abelian categories are additive categories where morphisms have kernels and cokernels, enabling exact sequences crucial for homological algebra. Small categories consist of objects and morphisms forming a set rather than a proper class, emphasizing foundational aspects in category theory. Understanding Abelian categories involves exploring their structure in additive settings, while small categories focus on size constraints impacting categorical constructions.
Defining Abelian Categories
Abelian categories are additive categories with kernels and cokernels, where every monomorphism and epimorphism is normal, enabling exact sequence formulations essential in homological algebra. Small categories, by contrast, are defined by having a set (rather than a proper class) of objects and morphisms, focusing on size rather than algebraic structure. The defining feature of an Abelian category lies in its ability to generalize modules over rings, incorporating exactness, biproducts, and the existence of both kernels and cokernels.
Defining Small Categories
Small categories are defined as categories whose collection of objects and morphisms both form sets, rather than proper classes, ensuring manageable size within set theory. Abelian categories, in contrast, are additive categories with exact sequences, enriched by kernels and cokernels, but their size is not necessarily small. Understanding small categories is fundamental for category theory's foundations, as this notion restricts categories to those accessible within standard set-theoretic frameworks.
Key Properties of Abelian Categories
Abelian categories are enriched with exact sequences, kernels, cokernels, and biproducts, enabling a robust framework for homological algebra, unlike small categories which are defined by the size constraint on their objects and morphisms. Key properties of Abelian categories include the existence of all finite limits and colimits, the fact that every monomorphism and epimorphism is normal, and that every morphism decomposes uniquely into an epimorphism followed by a monomorphism. These structures make Abelian categories essential for studying modules, sheaves, and derived functors in algebra and topology.
Key Characteristics of Small Categories
Small categories are categories whose collections of objects and morphisms form sets rather than proper classes, ensuring manageability in size and foundational simplicity. They possess key characteristics such as closure under composition, existence of identity morphisms for each object, and associativity of morphisms, aligning with the basic axioms of category theory. Unlike Abelian categories, which emphasize additive structures and exact sequences, small categories focus primarily on the size restriction and fundamental structural properties without imposing additional algebraic conditions.
Differences between Abelian and Small Categories
Abelian categories are additive categories with kernels and cokernels where every monomorphism and epimorphism is normal, enabling a rich theory of exact sequences and homological algebra. Small categories are categories whose collections of objects and morphisms form sets, emphasizing size constraints without imposing algebraic structure or exactness properties. The fundamental difference lies in Abelian categories' algebraic framework supporting homological operations versus small categories' focus on cardinality without additional structure.
Examples of Abelian Categories
Examples of Abelian categories include the category of abelian groups, the category of modules over a ring, and the category of coherent sheaves on a smooth projective variety, each characterized by exact sequences and kernels that enable homological algebra techniques. Small categories, in contrast, are defined by having a set of objects, but do not necessarily possess the exact structure required for an abelian category. Abelian categories provide a rich framework for studying complex algebraic structures through morphisms and exactness, which is crucial in areas like algebraic geometry and homological algebra.
Examples of Small Categories
Small categories are categories whose objects and morphisms both form sets rather than proper classes, making them manageable in size and suitable for concrete examples. Examples of small categories include the category of finite sets, finite groups, or any category constructed from a finite diagram such as a partially ordered set viewed as a category. Unlike Abelian categories, which require additive and exact structure for homological algebra, small categories emphasize size constraints and serve as foundational models in category theory.
Applications in Mathematics
Abelian categories provide a framework for homological algebra, enabling rigorous treatment of exact sequences and derived functors, essential in algebraic geometry and representation theory. Small categories, with a set of objects and morphisms, serve as foundational structures in category theory, allowing for categorical constructions and functorial analysis across various mathematical disciplines. Applications of Abelian categories often involve cohomology theories and module categories, while small categories facilitate the study of algebraic topology, category-based algebra, and the formalization of mathematical concepts.
Summary: Choosing Between Abelian and Small Categories
Abelian categories provide a rich structure ideal for homological algebra due to their additive nature and exact sequences, making them essential in modules and sheaf theory. Small categories focus on size, with objects and morphisms forming a set, facilitating foundational work in category theory and limiting complexity. Choosing between Abelian and small categories depends on the need for algebraic structure versus set-theoretic simplicity within the categorical framework.
Abelian category Infographic
 libterm.com
libterm.com