Adjoint functors are pairs of functors that establish a precise correspondence between categories, capturing a universal property that relates objects and morphisms in a structured way. They play a crucial role in category theory by enabling the construction of limits, colimits, and other fundamental concepts in mathematics and computer science. Explore the article to understand how adjoint functors connect different mathematical structures and enhance your comprehension of categorical relationships.
Table of Comparison
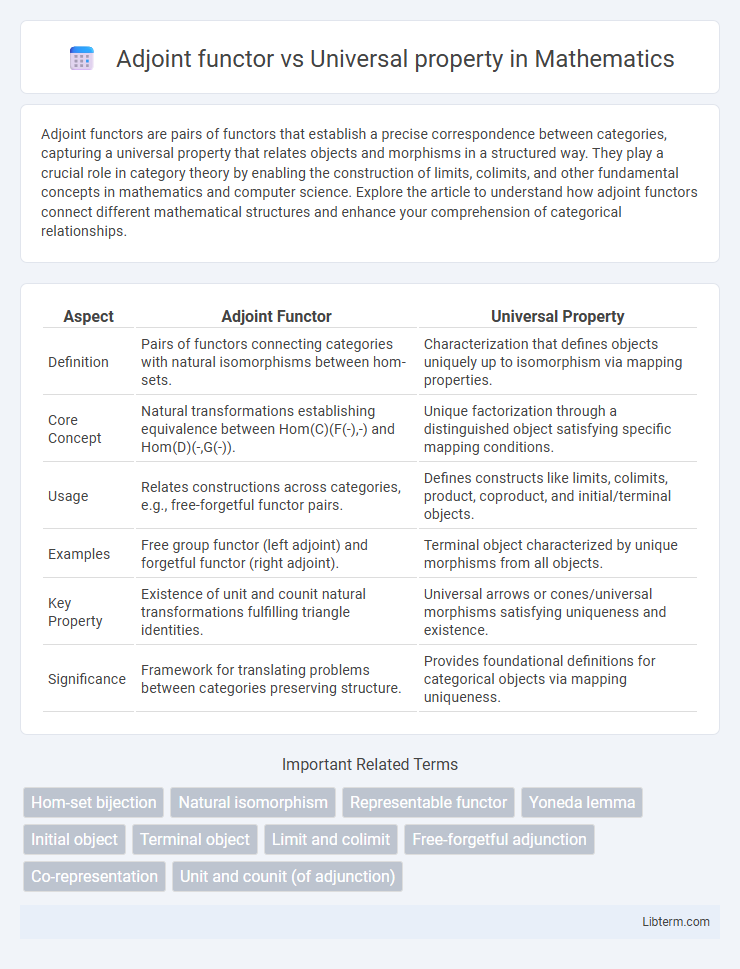
| Aspect | Adjoint Functor | Universal Property |
|---|---|---|
| Definition | Pairs of functors connecting categories with natural isomorphisms between hom-sets. | Characterization that defines objects uniquely up to isomorphism via mapping properties. |
| Core Concept | Natural transformations establishing equivalence between Hom(C)(F(-),-) and Hom(D)(-,G(-)). | Unique factorization through a distinguished object satisfying specific mapping conditions. |
| Usage | Relates constructions across categories, e.g., free-forgetful functor pairs. | Defines constructs like limits, colimits, product, coproduct, and initial/terminal objects. |
| Examples | Free group functor (left adjoint) and forgetful functor (right adjoint). | Terminal object characterized by unique morphisms from all objects. |
| Key Property | Existence of unit and counit natural transformations fulfilling triangle identities. | Universal arrows or cones/universal morphisms satisfying uniqueness and existence. |
| Significance | Framework for translating problems between categories preserving structure. | Provides foundational definitions for categorical objects via mapping uniqueness. |
Introduction to Adjoint Functors
Adjoint functors arise naturally in category theory, establishing a precise relationship between two categories via a pair of functors that are each other's best approximations. They capture the concept of universal construction by formalizing how certain objects can be characterized uniquely through hom-set isomorphisms, reflecting the underlying universal property. This correspondence simplifies complex categorical structures, enabling a deeper understanding of morphisms and natural transformations across diverse mathematical contexts.
Understanding Universal Properties
Universal properties characterize mathematical objects uniquely up to isomorphism by expressing their optimal or canonical relationships within a category. Adjoint functors arise naturally from universal properties, as they formalize the idea of best approximations or solutions to certain problems through pairs of functors that stand in a specific correspondence. Understanding universal properties is crucial for grasping how adjoint functors capture fundamental constructions in category theory, such as limits, colimits, and free objects.
Core Concepts: Functors and Categories
Adjoint functors are pairs of functors between categories that establish a precise correspondence between morphisms, capturing a universal relationship fundamental to category theory. The universal property characterizes objects or morphisms uniquely up to isomorphism by expressing a universal mapping condition within a category. Both concepts revolve around functors and categories, with adjoint functors providing a categorical framework that encodes universal properties through natural isomorphisms of Hom-sets.
Formal Definition of Adjoint Functors
An adjoint functor pair (F G) between categories C and D consists of two functors F: C - D and G: D - C, such that for every object c in C and d in D, there is a natural isomorphism Hom_D(F(c), d) Hom_C(c, G(d)). This natural bijection characterizes the adjunction and encodes the universal property that F is left adjoint to G, making G a right adjoint. The definition emphasizes the role of natural transformations and hom-set correspondences, distinguishing adjoint functors as a profound categorical concept underpinning universal constructions.
The Essence of Universal Properties
Universal properties characterize mathematical objects by their unique mapping properties within a category, providing canonical solutions to specific problems. They encapsulate existence and uniqueness in terms of representable functors, forming the foundational concept behind adjoint functors. Adjoint functors arise naturally from universal properties by establishing a correspondence between hom-sets that respect these canonical universal constructions.
Relationship Between Adjoint Functors and Universal Properties
Adjoint functors can be characterized by universal properties that specify unique morphisms satisfying certain conditions, making the concept of adjoints deeply intertwined with universal constructions. Each adjunction corresponds to a pair of functors where the unit and counit natural transformations embody universal properties enabling the bijection of hom-sets. Understanding the relationship between adjoint functors and universal properties reveals how these categorical structures encode optimal solutions to diagrammatic problems in category theory.
Key Examples in Category Theory
The adjoint functor pairs such as the free-forgetful adjunction between Set and Groups illustrate the universal property of free groups, characterizing objects via unique morphisms from free constructions. Another key example is the product in a category, defined by a universal property stating the existence of a unique cone mapping to the product from any object with projections, corresponding to a right adjoint to the diagonal functor. These examples demonstrate how adjoint functors encapsulate universal properties by establishing natural isomorphisms between hom-sets, fundamentally linking construction processes with uniqueness criteria in category theory.
Practical Applications of Adjoint Functors
Adjoint functors are instrumental in category theory and algebraic topology for constructing objects universally characterized by their mapping properties, streamlining solutions to optimization problems and homological algebra. Practical applications include defining free objects, such as free groups or free modules, where the adjunction provides a systematic way to embed elements while preserving essential structures. This framework also facilitates the development of sheaf theory and database theory by encoding constraints and dependencies through the universal properties tied to adjoints.
Comparing Structural Features
Adjoint functors characterize a pair of categories by establishing a natural isomorphism between hom-sets, reflecting a precise correspondence of morphisms that preserves structural relationships. Universal properties define objects up to unique isomorphism by specifying their interaction with other objects through a universal mapping condition, emphasizing existence and uniqueness in constructions. Both concepts capture fundamental categorical structures, with adjoint functors providing a bidirectional framework for morphism correspondence, whereas universal properties focus on the defining optimality and uniqueness of objects within categorical diagrams.
Summary and Further Resources
Adjoint functors characterize a pair of functors between categories that reflect universal properties through natural isomorphisms, providing a framework to represent solutions to optimization or extension problems. Universal properties define objects uniquely up to isomorphism by their relationships to other objects, forming the foundation for constructing adjoint pairs by capturing minimal or maximal conditions. For deeper understanding, consult Mac Lane's "Categories for the Working Mathematician" and Awodey's "Category Theory," as well as online lecture notes and research articles from nLab.
Adjoint functor Infographic
 libterm.com
libterm.com