A normal subgroup is a subgroup invariant under conjugation by any element of the parent group, meaning its left and right cosets coincide. This property enables the construction of quotient groups, which are fundamental in group theory for analyzing group structure. Explore the rest of the article to understand how normal subgroups shape group theory's landscape and impact your study of algebraic systems.
Table of Comparison
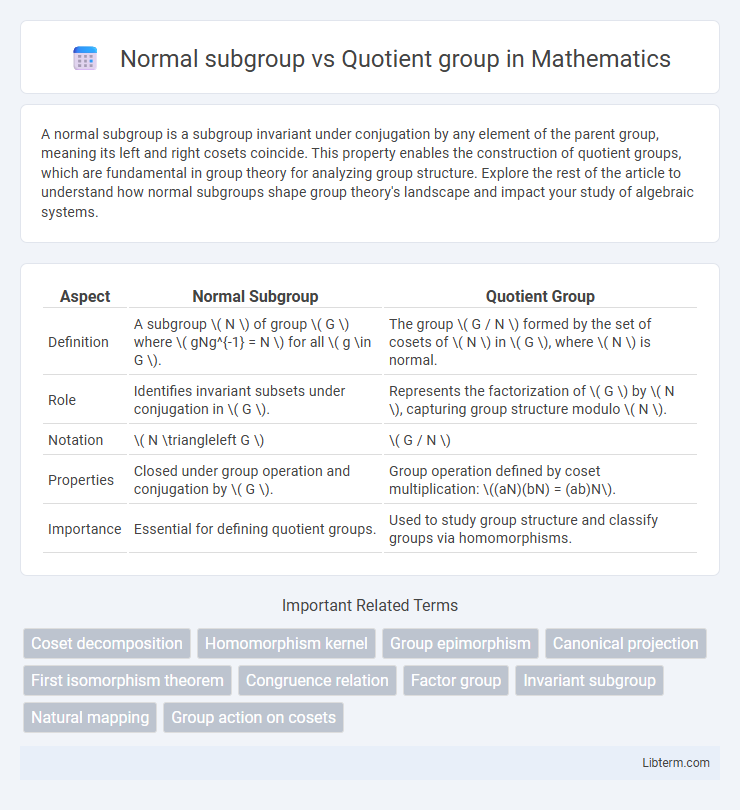
| Aspect | Normal Subgroup | Quotient Group |
|---|---|---|
| Definition | A subgroup \( N \) of group \( G \) where \( gNg^{-1} = N \) for all \( g \in G \). | The group \( G / N \) formed by the set of cosets of \( N \) in \( G \), where \( N \) is normal. |
| Role | Identifies invariant subsets under conjugation in \( G \). | Represents the factorization of \( G \) by \( N \), capturing group structure modulo \( N \). |
| Notation | \( N \triangleleft G \) | \( G / N \) |
| Properties | Closed under group operation and conjugation by \( G \). | Group operation defined by coset multiplication: \((aN)(bN) = (ab)N\). |
| Importance | Essential for defining quotient groups. | Used to study group structure and classify groups via homomorphisms. |
Introduction to Group Theory
A normal subgroup is a subgroup N of a group G that is invariant under conjugation by elements of G, meaning gNg-1 = N for all g in G, which allows the construction of the quotient group G/N. The quotient group G/N consists of the cosets of N in G, with the group operation defined as (aN)(bN) = (ab)N, effectively partitioning G into distinct equivalence classes based on N. Understanding normal subgroups and quotient groups is fundamental in group theory as they facilitate the study of group structure and enable the classification of groups through homomorphic images.
Definition of Normal Subgroup
A normal subgroup is defined as a subgroup \(N\) of a group \(G\) such that for every element \(g \in G\), the conjugate \(gNg^{-1}\) is contained in \(N\), ensuring invariance under conjugation. This property allows the construction of a quotient group \(G/N\), where the elements are the cosets of \(N\) in \(G\) and the group operation is well-defined. Normal subgroups are crucial in group theory because they facilitate the formation of homomorphic images and simplify the analysis of group structure.
Properties of Normal Subgroups
Normal subgroups are characterized by being invariant under conjugation by any group element, ensuring that for every element \( n \) in the normal subgroup \( N \) and every \( g \) in the parent group \( G \), the element \( gng^{-1} \) also lies in \( N \). This property guarantees that the set of left cosets coincides with the set of right cosets, enabling the construction of the quotient group \( G/N \). The quotient group inherits a well-defined group structure where the operation on cosets is consistent, stemming directly from the normality condition of the subgroup.
Definition of Quotient Group
A quotient group is formed by partitioning a group G into cosets of a normal subgroup N, where the set of these cosets inherits a group structure under the operation defined by (aN)(bN) = (ab)N. The normality of N ensures that the product of two cosets is well-defined and independent of representatives chosen from each coset. This construction creates a new group G/N, representing the original group's structure modulo the subgroup N.
Construction of Quotient Groups
A normal subgroup \( N \) of a group \( G \) allows the construction of a quotient group \( G/N \), which consists of cosets \( gN \) for \( g \in G \). The quotient group \( G/N \) inherits group operations defined by \( (gN)(hN) = (gh)N \), ensuring well-defined multiplication due to the normality of \( N \). This construction is fundamental for analyzing group structures via homomorphisms and for simplifying complex groups into more manageable quotient groups.
Relationship between Normal Subgroups and Quotient Groups
A normal subgroup \( N \) of a group \( G \) satisfies the condition \( gNg^{-1} = N \) for all \( g \in G \), ensuring that the set of left cosets coincides with the set of right cosets. The quotient group \( G/N \) comprises these cosets as elements, with group operation defined by \((aN)(bN) = (ab)N\), preserving the group structure. The existence of a normal subgroup \( N \) is both a necessary and sufficient condition for \( G/N \) to form a well-defined quotient group, establishing a fundamental link between subgroup normality and factor groups.
Examples of Normal Subgroups and Quotient Groups
In the group \( \mathbb{Z} \) of integers under addition, \( 3\mathbb{Z} \) is a normal subgroup whose corresponding quotient group \( \mathbb{Z}/3\mathbb{Z} \) consists of cosets \( \{0+3\mathbb{Z}, 1+3\mathbb{Z}, 2+3\mathbb{Z}\} \). In the symmetric group \( S_4 \), the Klein four-group \( V_4 = \{e, (12)(34), (13)(24), (14)(23)\} \) is a normal subgroup, and the quotient group \( S_4 / V_4 \) has order 6, isomorphic to \( S_3 \). The key property of normal subgroups is that their left and right cosets coincide, enabling the well-defined group structure on the set of cosets forming the quotient group.
Significance in Abstract Algebra
Normal subgroups are fundamental in abstract algebra because they allow the construction of quotient groups, which are essential for analyzing group structure and simplifying complex groups. A normal subgroup \(N\) of a group \(G\) ensures that the set of cosets \(G/N\) forms a well-defined quotient group, capturing the idea of partitioning the group into equivalence classes consistent with the group operation. Quotient groups facilitate the study of homomorphisms, factor groups, and the classification of groups via isomorphism theorems, making them pivotal in advanced algebraic theories.
Applications in Mathematics and Beyond
Normal subgroups are fundamental in constructing quotient groups, which partition a group into distinct cosets, facilitating the analysis of group structures and symmetries. Quotient groups play a crucial role in algebraic topology for defining fundamental groups and in Galois theory for understanding field extensions and solvability of polynomials. Beyond pure mathematics, these concepts are applied in cryptography for designing secure protocols and in physics for studying symmetry-breaking phenomena and particle interactions.
Key Differences and Summary
A normal subgroup \(N\) of a group \(G\) is a subgroup invariant under conjugation by elements of \(G\), meaning \(gNg^{-1} = N\) for all \(g \in G\). A quotient group \(G/N\) is the set of cosets of \(N\) in \(G\) equipped with group operation defined by \((gN)(hN) = (gh)N\), existing only when \(N\) is normal. The key difference lies in a normal subgroup being a specific subset of the original group, while the quotient group constructs a new group whose elements are cosets formed by this normal subgroup.
Normal subgroup Infographic
 libterm.com
libterm.com