The Ext functor measures the extent to which modules fail to be projective by classifying extensions between modules in homological algebra. It plays a critical role in understanding the relationships and structure of modules over a ring, especially in derived categories. Discover how the Ext functor can deepen your grasp of module theory by exploring the detailed explanations in the rest of this article.
Table of Comparison
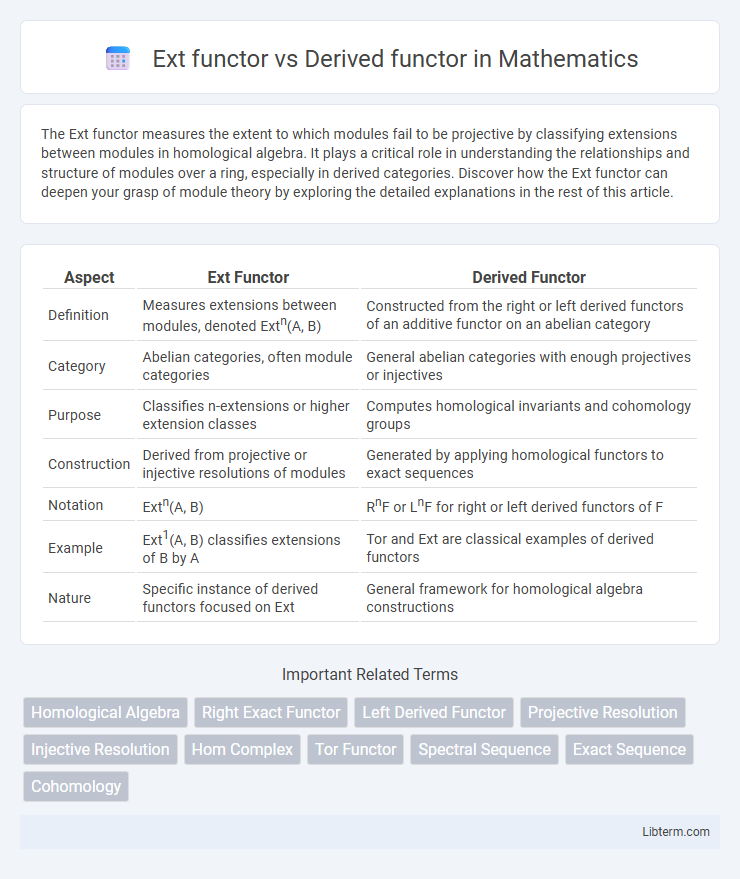
| Aspect | Ext Functor | Derived Functor |
|---|---|---|
| Definition | Measures extensions between modules, denoted Extn(A, B) | Constructed from the right or left derived functors of an additive functor on an abelian category |
| Category | Abelian categories, often module categories | General abelian categories with enough projectives or injectives |
| Purpose | Classifies n-extensions or higher extension classes | Computes homological invariants and cohomology groups |
| Construction | Derived from projective or injective resolutions of modules | Generated by applying homological functors to exact sequences |
| Notation | Extn(A, B) | RnF or LnF for right or left derived functors of F |
| Example | Ext1(A, B) classifies extensions of B by A | Tor and Ext are classical examples of derived functors |
| Nature | Specific instance of derived functors focused on Ext | General framework for homological algebra constructions |
Introduction to Ext Functor and Derived Functor
Ext functor measures extensions of modules by classifying equivalence classes of module extensions, playing a central role in homological algebra. Derived functors generalize classical functors, such as Hom, by systematically computing derived objects through projective or injective resolutions. The Ext functor arises as a specific derived functor of Hom, capturing higher-dimensional module extension data essential for understanding module structure and morphisms.
Fundamental Concepts in Homological Algebra
Ext functor is a key example of a derived functor that measures extensions between modules, capturing obstructions to lifting module homomorphisms. Derived functors generalize classical functors by systematically computing homology groups from projective or injective resolutions, revealing deeper algebraic structures. In homological algebra, understanding Ext as a derived functor of Hom elucidates relationships between module categories, enabling powerful classifications of module extensions and cohomology theories.
What is the Ext Functor?
The Ext functor is a fundamental tool in homological algebra that measures extensions between modules, capturing how one module can be embedded into another via exact sequences. It is defined as the right derived functor of the Hom functor, providing a systematic way to compute extension groups Ext^n(M, N) for modules M and N over a ring. Ext groups classify n-step extensions and detect obstructions to splitting, making them essential in understanding module structure and relationships in derived categories.
Understanding Derived Functors
Derived functors generalize classical homological constructions by extending functors to chain complexes, enabling the systematic calculation of objects like Ext and Tor groups. The Ext functor is a specific example of a derived functor arising from the right derived functors of Hom, capturing extension classes of modules over a ring. Understanding derived functors involves mastering projective and injective resolutions that allow the computation of these invariants in categories such as modules over a ring or sheaves on a topological space.
Construction and Computation of Ext
The Ext functor, derived from the Hom functor, measures extensions of modules and is constructed via projective or injective resolutions in homological algebra. Computationally, Ext groups Ext^n(M, N) are obtained by applying the Hom functor to a projective resolution of M or an injective resolution of N, followed by taking the n-th cohomology. Derived functors generalize this process by systematically capturing higher-dimensional data from non-exact functors, with Ext as a specific example illustrating the method of deriving functors to compute extension classes.
Derived Functors: Formal Definition and Examples
Derived functors generalize the notion of functors by capturing higher-dimensional homological information, constructed via resolutions in abelian categories. Formally, given a left exact functor \( F: \mathcal{A} \to \mathcal{B} \) between abelian categories, its right derived functors \( R^nF \) are defined by applying \( F \) to an injective resolution of an object in \( \mathcal{A} \) and taking the \( n \)-th cohomology. For example, the Ext functor \( \mathrm{Ext}^n_R(M, -) \) arises as the \(n\)-th right derived functor of the Hom functor \(\mathrm{Hom}_R(M, -)\) in module categories.
Key Differences Between Ext Functor and Derived Functor
Ext functor is a specific example of a derived functor measuring extensions between modules, particularly capturing classes of short exact sequences. Derived functors generalize homological constructions by systematically deriving functors to higher degrees, capturing more complex cohomological information. The key difference lies in Ext being a particular derived functor associated with Hom, while derived functors encompass a broader class, including Tor, cohomology, and beyond.
Applications in Module Theory and Algebraic Topology
Ext functors measure extensions of modules, classifying equivalence classes of module extensions and revealing obstructions in splitting sequences, critical for understanding module structure and homological dimensions. Derived functors generalize Ext by systematically constructing higher-order invariants from non-exact functors, facilitating the computation of homology and cohomology groups in algebraic topology. Applications in module theory include characterizing projective and injective modules, while in algebraic topology, derived functors translate topological spaces' homological properties into algebraic invariants through tools like spectral sequences.
Advantages and Limitations of Each Functor
The Ext functor provides a concrete method for classifying extensions of modules, offering explicit computations in homological algebra that are particularly useful for understanding module structures and their extensions. Derived functors generalize this approach, enabling the study of more complex homological properties through long exact sequences and allowing the systematic computation of cohomology beyond first-degree extensions. However, Ext functors are limited to extension classes and may fail to capture deeper or higher-dimensional homological relations, while derived functors can become computationally intensive and abstract, requiring projective or injective resolutions that complicate explicit calculations.
Conclusion: Choosing Between Ext and Derived Functors
Ext functors specifically measure extensions and classify module extensions, making them ideal for analyzing exact sequences and module structures. Derived functors provide a broader framework that generalizes homological constructions, useful for computing cohomology in various contexts beyond module extensions. Choosing between Ext and derived functors depends on the problem's focus: use Ext for explicit extension classification and derived functors for more comprehensive homological analyses.
Ext functor Infographic
 libterm.com
libterm.com