A principal bundle is a mathematical structure in differential geometry consisting of a total space, a base space, and a Lie group acting freely and transitively on the fibers. This concept plays a crucial role in gauge theory and the study of fiber bundles with group actions, providing a framework for understanding symmetry and connections. Explore the rest of the article to uncover how principal bundles underpin modern geometry and physics.
Table of Comparison
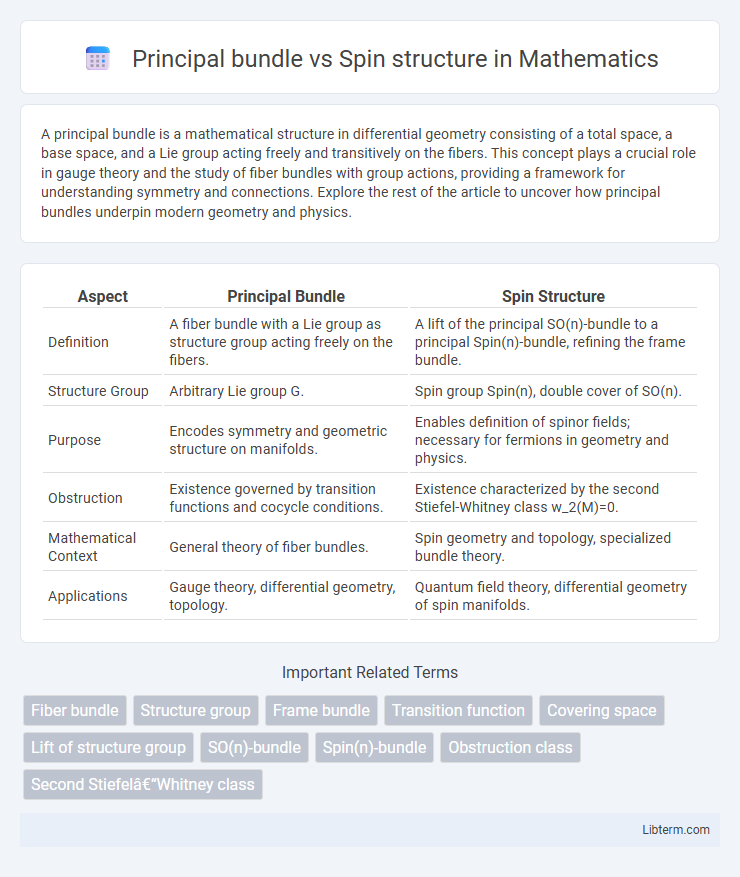
| Aspect | Principal Bundle | Spin Structure |
|---|---|---|
| Definition | A fiber bundle with a Lie group as structure group acting freely on the fibers. | A lift of the principal SO(n)-bundle to a principal Spin(n)-bundle, refining the frame bundle. |
| Structure Group | Arbitrary Lie group G. | Spin group Spin(n), double cover of SO(n). |
| Purpose | Encodes symmetry and geometric structure on manifolds. | Enables definition of spinor fields; necessary for fermions in geometry and physics. |
| Obstruction | Existence governed by transition functions and cocycle conditions. | Existence characterized by the second Stiefel-Whitney class w_2(M)=0. |
| Mathematical Context | General theory of fiber bundles. | Spin geometry and topology, specialized bundle theory. |
| Applications | Gauge theory, differential geometry, topology. | Quantum field theory, differential geometry of spin manifolds. |
Introduction to Principal Bundles
Principal bundles are fundamental geometric structures consisting of a total space, a base space, and a Lie group serving as the structure group that acts freely and transitively on the fibers. They generalize fiber bundles by incorporating group symmetries, enabling the formulation of gauge theories and connections on manifolds. Spin structures arise as special lifts of principal SO(n)-bundles to their double cover, the Spin(n) group, providing the necessary framework to define spinor fields in differential geometry and theoretical physics.
Understanding Spin Structures
Spin structures arise as lifts of the principal SO(n)-bundle of oriented orthonormal frames on a manifold to a principal Spin(n)-bundle, enabling the definition of spinor fields. Understanding Spin structures involves examining their existence conditions, characterized by the second Stiefel-Whitney class vanishing, and their role in allowing spin representations crucial for fermionic fields in geometry and physics. The distinction between a principal bundle and a Spin structure lies in the additional topological and algebraic constraints that enable Spin groups to serve as double covers of the special orthogonal groups.
The Role of the Structure Group
The structure group of a principal bundle defines the fiber's symmetries and governs how local trivializations intersect, while a Spin structure refines the principal SO(n)-bundle by lifting its structure group to the Spin group, which is a double cover of SO(n). This lift is crucial for defining spinor fields in differential geometry and theoretical physics, as Spin structures provide the necessary framework to describe fermions on manifolds. The existence of a Spin structure depends on the vanishing of the second Stiefel-Whitney class, linking topological properties of the principal SO(n)-bundle's structure group to the feasibility of this lift.
Principal Bundles in Differential Geometry
Principal bundles are fundamental objects in differential geometry that consist of a total space equipped with a smooth, free action of a Lie group G, projecting onto a base manifold M. They provide a framework for defining geometric structures and connections, serving as the underlying setup for gauge theories and characteristic classes. Unlike spin structures, which are specific lifts of the frame bundle to the Spin group to handle spinors, principal bundles are more general and include any Lie group symmetries acting smoothly on manifolds.
Spin Groups and Their Significance
Spin groups, denoted as Spin(n), serve as double covers of the special orthogonal groups SO(n) and are fundamental in defining spin structures on principal bundles. A spin structure is essentially a lift of the SO(n)-principal bundle associated with a manifold's tangent bundle to a Spin(n)-principal bundle, enabling the definition of spinor fields crucial for fermionic field theories. The significance of spin groups lies in their ability to resolve topological obstructions in orientable manifolds, allowing for the consistent formulation of quantum fields with half-integer spin through spin geometry and representation theory.
Relationship Between Principal Bundles and Spin Structures
Spin structures arise as lifts of principal SO(n)-bundles to principal Spin(n)-bundles, enabling the definition of spinor fields on manifolds. The principal bundle associated to the frame bundle underlies the construction of the spin structure by a double covering group homomorphism Spin(n) - SO(n). This relationship is fundamental in differential geometry and theoretical physics, especially in the study of manifolds with spinors and fermions.
Existence Conditions and Obstructions
Principal bundles require the structure group to act freely and transitively on the fibers, with their existence determined by characteristic classes such as Chern or Stiefel-Whitney classes. Spin structures exist as lifts of the principal SO(n)-bundle to a Spin(n)-bundle, and their existence is obstructed by the second Stiefel-Whitney class \( w_2 \) vanishing on the manifold. Obstructions to Spin structures highlight topological constraints in the underlying manifold, making \( w_2 = 0 \) the key criterion for the existence of a Spin structure.
Applications in Topology and Physics
Principal bundles provide the foundational framework for describing fiber bundles with a continuous group action, playing a crucial role in gauge theory and the study of characteristic classes in topology. Spin structures, which are liftings of the frame bundle to the Spin group, enable the definition of spinor fields essential for describing fermions in quantum field theory and the analysis of Dirac operators in differential geometry. Both tools facilitate the understanding of topological obstructions and anomalies in physics, with principal bundles capturing gauge symmetries and spin structures ensuring the consistent formulation of spinors on manifolds.
Comparing Principal Bundles and Spin Structures
Principal bundles serve as the foundational framework in differential geometry, characterized by a smooth manifold equipped with a continuous group action, typically a Lie group like SO(n). Spin structures refine principal SO(n)-bundles by lifting them to the Spin(n) group, a universal cover of SO(n), enabling the definition of spinor fields on manifolds. Unlike general principal bundles, spin structures exist only under specific topological conditions related to the second Stiefel-Whitney class, ensuring orientability and the existence of spinor representations essential in quantum field theory and differential topology.
Summary and Further Directions
Principal bundles provide the foundational framework for describing geometric structures on manifolds by encoding symmetry groups as fibers, while Spin structures refine this concept by lifting the frame bundle to its double cover, enabling the definition of spinors and addressing topological obstructions in orientable manifolds. The study of Spin structures is pivotal for understanding fermionic fields in quantum field theory and for the classification of manifolds in differential topology. Future research aims to explore generalized Spin structures in higher dimensions, their role in string theory, and connections with non-commutative geometry and index theory.
Principal bundle Infographic
 libterm.com
libterm.com