Linear functions are foundational in mathematics, representing relationships where variables change at a constant rate. They are characterized by a straight-line graph and an equation of the form y = mx + b, where m is the slope and b is the y-intercept. Explore the rest of this article to deepen your understanding of linear functions and their real-world applications.
Table of Comparison
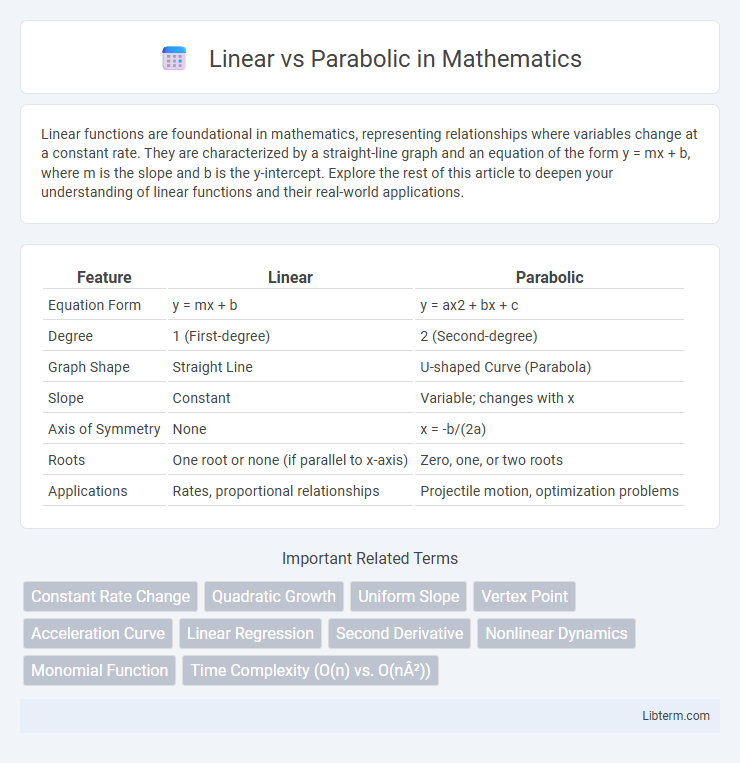
| Feature | Linear | Parabolic |
|---|---|---|
| Equation Form | y = mx + b | y = ax2 + bx + c |
| Degree | 1 (First-degree) | 2 (Second-degree) |
| Graph Shape | Straight Line | U-shaped Curve (Parabola) |
| Slope | Constant | Variable; changes with x |
| Axis of Symmetry | None | x = -b/(2a) |
| Roots | One root or none (if parallel to x-axis) | Zero, one, or two roots |
| Applications | Rates, proportional relationships | Projectile motion, optimization problems |
Introduction to Linear vs Parabolic Concepts
Linear equations represent relationships where the rate of change is constant, resulting in a straight-line graph defined by the equation y = mx + b. Parabolic equations, characterized by quadratic expressions such as y = ax^2 + bx + c, display a curved, U-shaped graph known as a parabola due to the variable being squared. Understanding these fundamental differences is crucial for interpreting their applications in physics, economics, and engineering.
Defining Linear Structures
Linear structures are characterized by elements arranged in a sequential, one-dimensional order where each item is connected to its predecessor and successor, such as arrays and linked lists. This organization enables straightforward traversal and manipulation, optimizing efficiency for operations like searching and insertion. In contrast, parabolic or nonlinear structures expand beyond linearity to include hierarchical or networked connections, serving different computational and organizational needs.
Understanding Parabolic Structures
Parabolic structures efficiently distribute loads by following the natural path of tension and compression forces, minimizing bending moments and material usage. Unlike linear elements that resist loads through uniform stress distribution, parabolic arches adapt to varying load intensities, resulting in enhanced structural stability and durability. Engineers utilize parabolic curves in bridges and roofs to optimize strength, reduce deflections, and achieve aesthetically pleasing designs with superior load-bearing capacities.
Key Differences Between Linear and Parabolic
Linear functions exhibit a constant rate of change, represented by straight lines with a uniform slope, while parabolic functions are quadratic, characterized by a variable rate of change and curved graphs with a distinct vertex. In linear equations, the highest exponent of the variable is one, contrasting with parabolic equations where the highest exponent is two, impacting the shape and properties of the graph. Linear models best describe uniform growth or decline scenarios, whereas parabolic models effectively capture acceleration or deceleration patterns in phenomena like projectile motion or quadratic optimization problems.
Applications of Linear Models
Linear models are extensively applied in fields such as economics for demand forecasting, physics for motion analysis, and environmental science for modeling pollutant dispersion. Their simplicity allows for efficient computation and clear interpretation, making them ideal for real-time decision-making in finance and operations research. Linear regression also plays a crucial role in predictive analytics, enabling businesses to identify trends and optimize strategic planning effectively.
Applications of Parabolic Models
Parabolic models are widely applied in physics and engineering fields such as projectile motion, where objects follow a curved trajectory under constant acceleration due to gravity. They are essential in optimizing design parameters for satellite dishes and car headlights, which focus signals and light along a parabolic curve for maximum efficiency. Parabolic equations also model heat distribution and diffusion processes, enabling precise simulations in material science and environmental studies.
Advantages of Linear Approaches
Linear approaches offer simplicity and computational efficiency, making them ideal for large datasets and real-time applications. They provide interpretable models with straightforward parameter estimation, facilitating easier debugging and implementation. Their scalability and robustness to overfitting enhance performance in high-dimensional spaces where parabolic methods may become computationally intensive.
Benefits of Parabolic Approaches
Parabolic approaches enhance modeling accuracy by capturing nonlinear relationships that linear methods often miss, improving prediction quality in complex datasets. These techniques enable better optimization in various fields, such as finance and engineering, by accommodating variable rates of change and curvature in data trends. Parabolic models also offer flexibility in fitting data patterns, leading to more robust and reliable analytical outcomes.
Choosing Between Linear and Parabolic Solutions
Choosing between linear and parabolic solutions depends on the problem's complexity and accuracy requirements. Linear models offer simplicity and faster computation for problems with proportional relationships, while parabolic models capture curvature and non-linear dynamics, enhancing precision in scenarios like projectile motion or optimization curves. Evaluating the trade-off between computational efficiency and model fidelity guides the selection to best fit specific engineering, physics, or data modeling applications.
Conclusion: Linear vs Parabolic Analysis
Linear models offer simplicity and faster computation but often lack the flexibility to capture complex patterns in data, leading to underfitting in nonlinear scenarios. Parabolic models, by incorporating quadratic terms, provide a more accurate representation of curvature and relationships, improving fit for datasets with nonlinear trends. Choosing between linear and parabolic analysis depends on the trade-off between model interpretability and the need for capturing inherent data complexity.
Linear Infographic
 libterm.com
libterm.com