Curvature describes the amount by which a geometric object deviates from being flat or straight, playing a crucial role in fields like mathematics, physics, and engineering. Understanding curvature helps you analyze shapes, surfaces, and the bending of materials or space, influencing design and scientific models. Explore the rest of the article to discover the different types of curvature and their real-world applications.
Table of Comparison
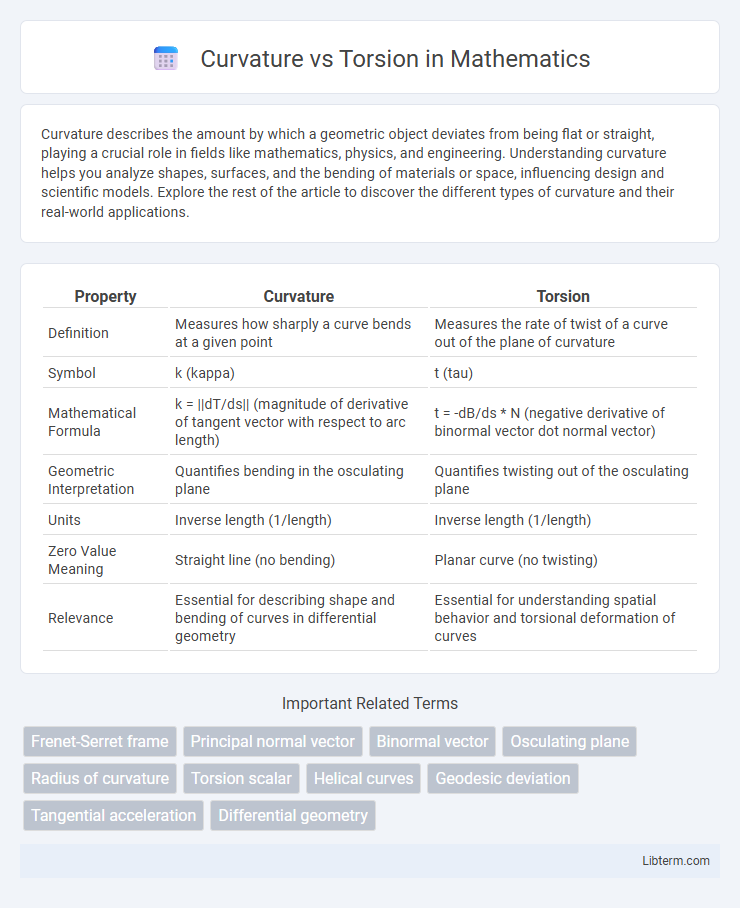
| Property | Curvature | Torsion |
|---|---|---|
| Definition | Measures how sharply a curve bends at a given point | Measures the rate of twist of a curve out of the plane of curvature |
| Symbol | k (kappa) | t (tau) |
| Mathematical Formula | k = ||dT/ds|| (magnitude of derivative of tangent vector with respect to arc length) | t = -dB/ds * N (negative derivative of binormal vector dot normal vector) |
| Geometric Interpretation | Quantifies bending in the osculating plane | Quantifies twisting out of the osculating plane |
| Units | Inverse length (1/length) | Inverse length (1/length) |
| Zero Value Meaning | Straight line (no bending) | Planar curve (no twisting) |
| Relevance | Essential for describing shape and bending of curves in differential geometry | Essential for understanding spatial behavior and torsional deformation of curves |
Introduction to Curvature and Torsion
Curvature measures how quickly a curve deviates from being a straight line, quantifying the rate of change of the tangent vector with respect to arc length. Torsion quantifies the rate at which a curve twists out of the plane of curvature, representing the change in the binormal vector along the curve. Both curvature and torsion provide essential geometric properties that fully describe the three-dimensional shape and behavior of a space curve.
Definitions: What is Curvature?
Curvature measures the rate at which a curve deviates from being a straight line at a given point, quantifying how sharply it bends. It is mathematically defined as the magnitude of the derivative of the unit tangent vector with respect to arc length. Curvature is a scalar value that captures the intrinsic geometric property of a curve independent of its parametrization.
Defining Torsion in Differential Geometry
Torsion in differential geometry measures how a space curve deviates from being planar by quantifying its rate of twist around the tangent vector. It is defined using the derivative of the binormal vector with respect to arc length, specifically as the scalar quantity t = -dB/ds * N, where B is the binormal and N is the principal normal. Unlike curvature, which describes how sharply a curve bends, torsion captures the three-dimensional twisting behavior essential for characterizing the full spatial geometry of curves.
Geometric Interpretation: Curvature vs Torsion
Curvature measures the rate at which a curve deviates from being a straight line in a plane, quantifying the bending of the curve at a given point. Torsion quantifies the rate at which a curve departs from being planar by measuring the twist or spatial distortion of the curve in three-dimensional space. Together, curvature and torsion provide a complete geometric characterization of a space curve's shape and behavior.
Mathematical Formulations and Equations
Curvature (k) quantifies the rate of change of the tangent vector with respect to arc length, defined mathematically as k = |dT/ds|, where T is the unit tangent vector and s is the arc length parameter. Torsion (t) measures the rate of change of the binormal vector, expressed as t = - (dB/ds) * N, with B as the binormal vector and N as the principal normal vector. The Frenet-Serret formulas formally relate curvature and torsion to the derivatives of the orthonormal frame {T, N, B}, encapsulated in the system: dT/ds = kN, dN/ds = -kT + tB, and dB/ds = -tN.
Physical Examples: Real-World Applications
Curvature measures how sharply a curve bends in space, while torsion quantifies the rate at which the curve twists out of the plane of curvature. In engineering, curvature is critical for designing roads and railways to ensure smooth, safe turns, whereas torsion is essential in the analysis of springs and helical structures, affecting their mechanical stability. In biomechanics, curvature and torsion describe the shape and movement of DNA strands and the spinal column, influencing flexibility and resistance to deformation.
Differences between Curvature and Torsion
Curvature measures how sharply a curve bends at a given point, quantifying the rate of change of the tangent vector with respect to arc length. Torsion measures the rate at which a curve twists out of the plane of curvature, reflecting the deviation from being planar. While curvature is always non-negative and relates to bending, torsion can be positive, negative, or zero and captures the three-dimensional twisting behavior of the curve.
Visualizing Curves: 2D vs 3D Perspectives
Curvature measures how sharply a curve bends in a plane, easily visualized in 2D by the radius of an osculating circle, while torsion quantifies the twist of a curve out of the plane, essential for understanding 3D spatial behavior. In 2D, curvature alone describes the curve's shape, but 3D curves require both curvature and torsion to capture bending and twisting, enabling accurate visualization of complex trajectories. Tools like Frenet-Serret frames graphically represent curvature and torsion, enhancing the interpretation of curve geometry in multidimensional spaces.
Importance of Curvature and Torsion in Engineering
Curvature defines how sharply a curve bends, while torsion measures the twist of a curve out of its plane, both crucial for designing mechanical components and structural elements. Accurate calculation of curvature is essential for stress analysis in beams and bridges, ensuring material strength and stability under load. Torsion is vital in shaft design and aerospace engineering, as it affects the twisting behavior and overall integrity of rotating systems.
Conclusion: Key Insights on Curvature and Torsion
Curvature measures how sharply a curve bends, quantifying the deviation from being a straight line, while torsion assesses the rate of twist of the curve out of its osculating plane, reflecting its three-dimensional spatial behavior. High curvature indicates significant bending, whereas high torsion signifies pronounced twisting, both critical for characterizing the geometry of space curves in fields like differential geometry, robotics, and physics. Understanding the interplay between curvature and torsion enables precise modeling of complex shapes and motions, essential for applications such as path planning and structural analysis.
Curvature Infographic
 libterm.com
libterm.com