A ring symbolizes commitment, style, and personal expression, making it a timeless accessory for any occasion. Choosing the perfect ring involves understanding various styles, materials, and meanings behind each design. Explore the rest of the article to discover how to select a ring that truly reflects Your personality and intentions.
Table of Comparison
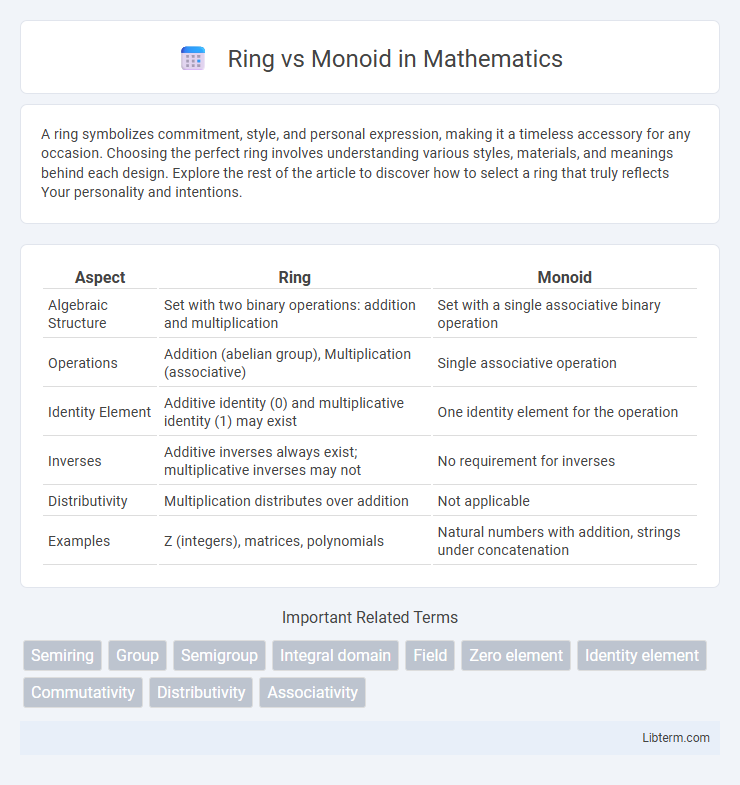
| Aspect | Ring | Monoid |
|---|---|---|
| Algebraic Structure | Set with two binary operations: addition and multiplication | Set with a single associative binary operation |
| Operations | Addition (abelian group), Multiplication (associative) | Single associative operation |
| Identity Element | Additive identity (0) and multiplicative identity (1) may exist | One identity element for the operation |
| Inverses | Additive inverses always exist; multiplicative inverses may not | No requirement for inverses |
| Distributivity | Multiplication distributes over addition | Not applicable |
| Examples | Z (integers), matrices, polynomials | Natural numbers with addition, strings under concatenation |
Introduction to Algebraic Structures
Rings and monoids are fundamental algebraic structures studied in abstract algebra, with rings combining two operations: addition and multiplication, where addition forms an abelian group and multiplication forms a monoid. Monoids consist of a single associative binary operation with an identity element, serving as a simpler structure compared to rings. Understanding the properties and differences between rings and monoids is essential for advancing in topics such as module theory, ring homomorphisms, and algebraic structures in computer science.
Defining Rings: Basics and Properties
Rings are algebraic structures consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group and multiplication is associative. Unlike monoids, which require only a single associative operation with an identity element, rings require additive inverses and distributive laws connecting multiplication and addition. The core properties defining rings include closure, associativity for both operations, the existence of additive identity and inverses, and distributive laws, distinguishing rings from other algebraic structures such as monoids.
Understanding Monoids: Key Features
Monoids are algebraic structures featuring a single associative binary operation and an identity element, essential for combining elements in a consistent manner. Unlike rings, monoids do not require inverses or a second operation, simplifying their structure while maintaining closure and associativity. This fundamental simplicity makes monoids crucial in computer science for modeling concatenation and accumulation processes.
Core Differences Between Rings and Monoids
Rings are algebraic structures consisting of two binary operations, addition and multiplication, where addition forms an abelian group and multiplication forms a monoid with distributive laws linking them. Monoids are simpler structures with a single associative binary operation and an identity element, lacking the additive inverse and distributive properties found in rings. The core difference lies in rings combining two operations with inverse and distributive requirements, while monoids focus solely on one operation with identity and associativity.
Examples of Rings in Mathematics
Examples of rings in mathematics include the set of integers \(\mathbb{Z}\) with standard addition and multiplication, the set of \(n \times n\) matrices over a field, and polynomial rings such as \(\mathbb{R}[x]\). These structures satisfy ring axioms by having two binary operations where addition forms an abelian group and multiplication is associative. Unlike monoids, rings require an additive inverse for each element, enriching the algebraic framework for applications in number theory and algebraic geometry.
Practical Applications of Monoids
Monoids serve as fundamental structures in computer science, enabling efficient data aggregation and parallel processing through their associative binary operation and identity element. Practical applications include string concatenation, merging data streams, and constructing foldable collections in functional programming languages like Haskell. These properties facilitate scalable algorithms for distributed computing, database query optimization, and event sourcing systems.
Structural Similarities and Overlaps
Rings and monoids share a common algebraic structure through their associative binary operations and the presence of an identity element, where monoids feature a single associative operation with an identity, and rings extend this by incorporating two operations--addition and multiplication--with addition forming an abelian group. Both structures emphasize closure, associativity, and identity properties, but rings require additive inverses and distributive laws connecting multiplication and addition, reflecting a deeper algebraic framework. The overlap exists in the multiplicative monoid within a ring, highlighting the monoid structure embedded in ring multiplication, enabling the exploration of algebraic properties such as unit elements and cancellation laws within ring theory.
The Role of Identity Elements
A ring contains two identity elements: the additive identity (0) and the multiplicative identity (1), where 0 serves as the additive identity for the abelian group structure under addition, and 1 is the multiplicative identity for the monoid structure under multiplication. A monoid requires only a single identity element that acts as the neutral element for its associative binary operation, typically denoted as e or 1. The dual identity elements in a ring enable both additive inverses and multiplicative closure, differentiating it from monoids which possess only one identity element associated with a single operation.
Abstract Algebra: Ring and Monoid Interactions
In abstract algebra, a ring consists of a set equipped with two binary operations: addition and multiplication, where the addition operation forms an abelian group and the multiplication operation forms a monoid. The monoid structure in a ring is defined by the associative multiplication with an identity element, differentiating it from general monoids that lack an additive group structure. Interactions between rings and monoids arise in the study of ring homomorphisms and monoid actions, providing a framework for exploring algebraic structures with combined additive and multiplicative properties.
Summary: Choosing Between Ring and Monoid
A ring combines two operations, addition and multiplication, with specific algebraic properties, making it ideal for complex structures like integers and matrices. A monoid involves a single associative operation with an identity element, suitable for simpler, single-operation systems like string concatenation or function composition. Selecting between a ring and a monoid depends on the need for dual operations with interactions (rings) versus a single associative operation with identity (monoids).
Ring Infographic
 libterm.com
libterm.com