Radical changes often challenge traditional perspectives, driving innovation and transforming industries. Embracing radical ideas can unlock new opportunities for growth and success in your personal and professional life. Explore the rest of this article to discover how radical approaches can redefine your future.
Table of Comparison
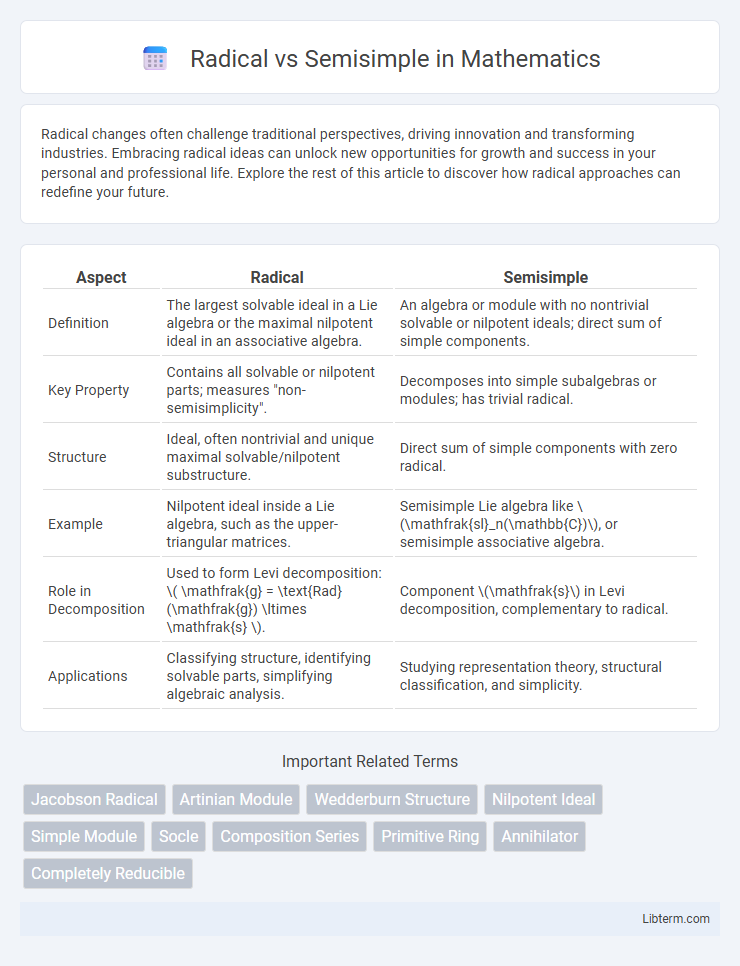
| Aspect | Radical | Semisimple |
|---|---|---|
| Definition | The largest solvable ideal in a Lie algebra or the maximal nilpotent ideal in an associative algebra. | An algebra or module with no nontrivial solvable or nilpotent ideals; direct sum of simple components. |
| Key Property | Contains all solvable or nilpotent parts; measures "non-semisimplicity". | Decomposes into simple subalgebras or modules; has trivial radical. |
| Structure | Ideal, often nontrivial and unique maximal solvable/nilpotent substructure. | Direct sum of simple components with zero radical. |
| Example | Nilpotent ideal inside a Lie algebra, such as the upper-triangular matrices. | Semisimple Lie algebra like \(\mathfrak{sl}_n(\mathbb{C})\), or semisimple associative algebra. |
| Role in Decomposition | Used to form Levi decomposition: \( \mathfrak{g} = \text{Rad}(\mathfrak{g}) \ltimes \mathfrak{s} \). | Component \(\mathfrak{s}\) in Levi decomposition, complementary to radical. |
| Applications | Classifying structure, identifying solvable parts, simplifying algebraic analysis. | Studying representation theory, structural classification, and simplicity. |
Introduction to Radical and Semisimple Concepts
The radical of an algebra is its largest solvable ideal, capturing the algebra's "non-semisimple" structure and serving as a measure of its deviation from simplicity. Semisimple algebras decompose into a direct sum of simple algebras, exhibiting no nonzero radical and ensuring complete reducibility of their representations. Understanding the radical and semisimple components provides critical insight into algebra classification, module theory, and representation decomposition.
Defining Radical Structures
Radical structures in algebra refer to maximal solvable ideals within a Lie algebra or maximal nilpotent ideals in associative algebras, capturing elements that obstruct semisimplicity. The radical serves as the largest "degenerate" component, isolating non-semiprimitive parts by containing all solvable or nilpotent substructures. Understanding the radical is crucial for decomposing algebras into a semisimple part and a radical, enabling classification and structural analysis in algebraic theory.
Understanding Semisimple Structures
Semisimple structures are characterized by their decomposition into a direct sum of simple modules, maximizing the presence of irreducible components and ensuring no non-trivial radicals exist. Understanding semisimple algebras requires recognizing that their radical, defined as the largest solvable ideal, is zero, which guarantees complete reducibility of modules. This property is crucial in representation theory, where semisimple modules admit a clean, well-understood classification through simple submodules.
Key Differences: Radical vs Semisimple
The radical of an algebra is its largest solvable ideal consisting of elements that act nilpotently, while a semisimple algebra decomposes into a direct sum of simple modules with no nontrivial solvable ideals. Radical algebras emphasize nilpotent behavior and lack complete reducibility, whereas semisimple algebras exhibit complete reducibility and zero radical, ensuring structural rigidity. Key differences lie in the presence of the radical ideal in radical algebras and its absence in semisimple ones, reflecting contrasting decomposition properties and module behaviors.
Historical Origins and Development
Radical and semisimple concepts originated in the classification of algebraic structures, tracing back to the early 20th century with contributions from Emil Artin and Joseph Wedderburn. The radical, defined as the maximal solvable ideal, evolved to capture the "non-simple" part of an algebra, while semisimple algebras, characterized by the absence of nontrivial solvable ideals, aligned with the structure theory of Lie algebras and associative algebras. These developments laid the groundwork for modern algebraic theories, influencing areas such as representation theory and the study of algebraic groups.
Mathematical Applications and Significance
Radical and semisimple structures play crucial roles in algebra, particularly in the classification and analysis of Lie algebras and associative algebras. The radical, often the largest solvable ideal, helps identify the "non-semisimple" part of an algebra, whereas semisimple components decompose into direct sums of simple algebras, enabling clearer structural understanding. These concepts aid in applications like representation theory, where semisimple algebras correspond to completely reducible representations, and in solving algebraic equations by separating complex systems into simpler, analyzable parts.
Radical and Semisimple in Algebra
The radical of an algebra is the largest solvable ideal that measures the "non-semisimple" part, often denoted as the Jacobson radical, while a semisimple algebra decomposes into a direct sum of simple algebras without a radical component. Semisimple algebras possess no nonzero solvable ideals, making their structure fully reducible into simple modules, whereas the radical captures nilpotent and solvable elements affecting this decomposition. Understanding the interplay between the radical and semisimple parts is fundamental in the Wedderburn-Artin theorem, which characterizes finite-dimensional associative algebras over a field as the direct sum of their radical and a semisimple subalgebra.
Examples of Radical and Semisimple Structures
Radical structures often include nilpotent Lie algebras, such as the Heisenberg algebra, where all elements are nilpotent and the algebra lacks nontrivial semisimple components. Semisimple Lie algebras, exemplified by sl(2, C) and so(3, R), decompose into direct sums of simple Lie algebras with no abelian or nilpotent ideals. The Levi decomposition theorem illustrates how every finite-dimensional Lie algebra over a field of characteristic zero splits into a semisimple subalgebra and its radical, exemplifying the interplay between radical and semisimple structures.
Implications in Modern Mathematics
The distinction between radical and semisimple components in algebraic structures underpins key developments in modern mathematics, influencing representation theory and module decomposition. Semisimple algebras provide a framework for classifying modules through complete reducibility, while radicals capture the "non-semisimple" deviations crucial to understanding extensions and morphisms. These concepts facilitate advancements in Lie algebra theory, algebraic groups, and category theory, enabling refined structural analysis and computational methods.
Conclusion: Choosing Between Radical and Semisimple
Choosing between radical and semisimple structures hinges on the desired algebraic properties and application context; radical components capture nilpotent behavior and complexity, while semisimple parts ensure decomposability into simple modules and facilitate classification. In representation theory and Lie algebra analysis, leveraging the semisimple quotient after factoring out the radical often simplifies problem-solving and theoretical insights. The balance depends on whether one prioritizes structural simplicity and direct sum decompositions or the detailed study of extensions and nilpotent elements inherent in the radical.
Radical Infographic
 libterm.com
libterm.com