Double pole switches are designed to control two separate circuits simultaneously, providing enhanced safety and functionality for electrical systems. They are commonly used in applications requiring isolation of both the live and neutral wires, such as in 240-volt appliances or complex home wiring setups. Explore this article to understand how double pole switches operate and ensure your electrical installations are both safe and efficient.
Table of Comparison
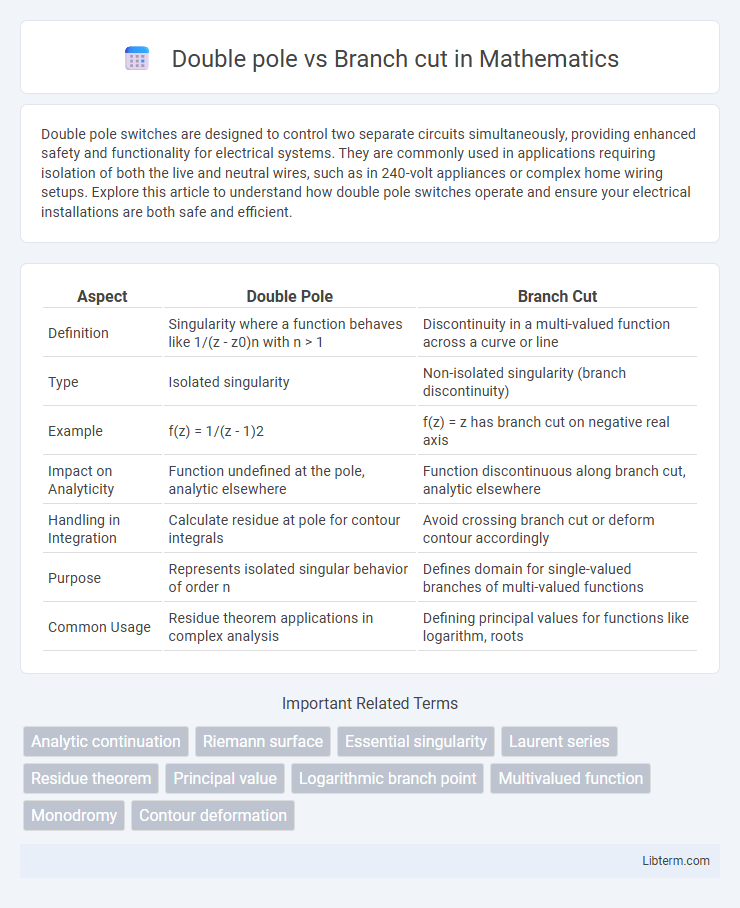
| Aspect | Double Pole | Branch Cut |
|---|---|---|
| Definition | Singularity where a function behaves like 1/(z - z0)n with n > 1 | Discontinuity in a multi-valued function across a curve or line |
| Type | Isolated singularity | Non-isolated singularity (branch discontinuity) |
| Example | f(z) = 1/(z - 1)2 | f(z) = z has branch cut on negative real axis |
| Impact on Analyticity | Function undefined at the pole, analytic elsewhere | Function discontinuous along branch cut, analytic elsewhere |
| Handling in Integration | Calculate residue at pole for contour integrals | Avoid crossing branch cut or deform contour accordingly |
| Purpose | Represents isolated singular behavior of order n | Defines domain for single-valued branches of multi-valued functions |
| Common Usage | Residue theorem applications in complex analysis | Defining principal values for functions like logarithm, roots |
Introduction to Double Poles and Branch Cuts
Double poles represent singularities where a function's value approaches infinity at a rate proportional to the inverse square of the distance to the pole, indicating a higher-order pole in complex analysis. Branch cuts define lines or curves on the complex plane along which a multi-valued function is discontinuous to ensure single-valued behavior on the chosen branch. Understanding double poles and branch cuts is essential for analyzing complex functions, integral evaluations, and conformal mappings in mathematical physics and engineering applications.
Mathematical Definitions: Double Pole vs Branch Cut
A double pole in complex analysis is a type of isolated singularity where a function behaves like \( \frac{1}{(z - z_0)^2} \) near the point \( z_0 \), characterized by the Laurent series containing a term with order \(-2\). A branch cut is a curve or line in the complex plane used to define a single-valued branch of a multi-valued function, such as the complex logarithm or root functions, by preventing discontinuities in the complex argument. While double poles represent isolated points with specific order singularities, branch cuts represent continuous discontinuities that resolve multi-valuedness in analytic continuation.
Analytic Functions and Their Singularities
Double poles represent isolated singularities where an analytic function diverges as the reciprocal of the square of the distance from the singularity, characterized by a Laurent series with a specific principal part. Branch cuts arise in multivalued analytic functions, such as complex logarithms or fractional powers, enabling a single-valued branch by removing discontinuities along a chosen curve in the complex plane. The distinction between double poles and branch cuts is crucial for contour integration and understanding function behavior near singular points, especially in complex analysis and residue calculus.
Visualizing Double Poles and Branch Cuts on the Complex Plane
Visualizing double poles on the complex plane reveals distinct behavior characterized by a point where a function's value tends toward infinity with a multiplicity of two, often depicted as a sharp, symmetric spike. Branch cuts, conversely, represent lines or curves on the complex plane that define discontinuities in multi-valued functions like the complex logarithm or square root, typically illustrated as a slit extending from a branch point to infinity or another branch point. Graphical tools often use color gradients or contour plots to differentiate double poles' localized singularities from branch cuts' extended discontinuities, enhancing comprehension of complex function structures.
Key Differences Between Double Poles and Branch Cuts
Double poles represent isolated singularities where a function's value becomes infinite more rapidly, characterized by terms like 1/(z-z0)2 in its Laurent series, while branch cuts correspond to discontinuities defining a function's multi-valued nature, often visualized as lines or curves on the complex plane to restore single-valued behavior. Double poles are localized points causing infinite residues and play a crucial role in contour integration and residue calculus, whereas branch cuts serve as domain restrictions to handle functions such as logarithms and fractional powers, preventing ambiguity in values. The key distinction lies in double poles being isolated singularities with finite, calculable residues contrasting with branch cuts being non-isolated, extended discontinuities that alter the topology of the function's domain.
Physical and Engineering Applications
Double poles in physical and engineering systems represent points where system responses exhibit higher-order resonance or instability, crucial for analyzing control systems and signal processing. Branch cuts typically arise in complex analysis related to multivalued functions, playing a fundamental role in defining phase shifts and wave behaviors in electromagnetic theory and fluid dynamics. Understanding double poles aids in predicting system behavior near resonance frequencies, while branch cuts enable accurate modeling of wave propagation and discontinuities in engineering applications.
Examples in Complex Integration
In complex integration, a double pole example occurs at \( z=0 \) for the function \( f(z)=\frac{1}{z^2} \), where the residue calculation involves the first derivative of the numerator. Branch cuts commonly appear for multi-valued functions like \( f(z)=\sqrt{z} \), with a typical branch cut taken along the negative real axis to make the function single-valued. When evaluating integrals using contour methods, residues at double poles provide exact contributions, whereas branch cuts require careful treatment of discontinuities across the chosen cut to properly define integrals.
Residue Calculus: Handling Double Poles vs Branch Cuts
Residue calculus treats double poles by computing the first derivative of the function multiplied by \((z - z_0)^2\) at the pole \(z_0\), yielding precise residue values crucial for contour integration. Branch cuts require defining a branch of the multi-valued function to avoid discontinuities, typically handled by choosing an appropriate contour that encircles the branch point without crossing the cut. While double poles offer isolated singularities with explicitly calculable residues, branch cuts introduce continuous spectra of singularities that necessitate integral approaches over branch boundaries.
Common Mistakes and Misconceptions
Double poles are often mistaken for simple poles with higher multiplicity, leading to errors in residue calculation and contour integration. Branch cuts are commonly misunderstood as actual discontinuities, whereas they represent a chosen boundary to make multi-valued functions like logarithms and roots single-valued. Confusing double poles with branch points causes improper analytic continuation and incorrect evaluation of integrals involving complex functions.
Conclusion: Summary and Practical Implications
Double poles result in more complex residue calculations and often signal repeated eigenvalues or resonances in physical systems, whereas branch cuts represent continuous spectra associated with multi-valued functions such as logarithms or square roots. Understanding the distinction is critical for accurate contour integration and evaluating inverse Laplace or Fourier transforms in applied mathematics and engineering. Practical implications include selecting appropriate methods for numerical integration and stability analysis in differential equations and signal processing.
Double pole Infographic
 libterm.com
libterm.com