The beta function is a special mathematical function defined by an integral that plays a key role in calculus, statistics, and various scientific computations. It is closely related to the gamma function and appears in probability theory, particularly in the context of beta distributions. Discover how the beta function can be applied and computed by exploring the rest of this article.
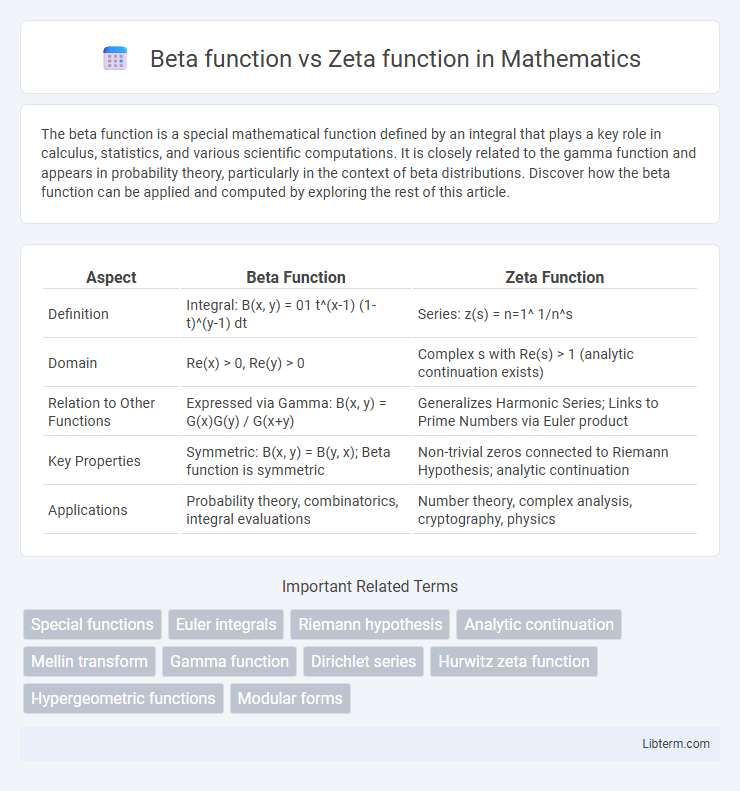
Table of Comparison
| Aspect | Beta Function | Zeta Function |
|---|---|---|
| Definition | Integral: B(x, y) = 01 t^(x-1) (1-t)^(y-1) dt | Series: z(s) = n=1^ 1/n^s |
| Domain | Re(x) > 0, Re(y) > 0 | Complex s with Re(s) > 1 (analytic continuation exists) |
| Relation to Other Functions | Expressed via Gamma: B(x, y) = G(x)G(y) / G(x+y) | Generalizes Harmonic Series; Links to Prime Numbers via Euler product |
| Key Properties | Symmetric: B(x, y) = B(y, x); Beta function is symmetric | Non-trivial zeros connected to Riemann Hypothesis; analytic continuation |
| Applications | Probability theory, combinatorics, integral evaluations | Number theory, complex analysis, cryptography, physics |
Introduction to Beta and Zeta Functions
The Beta function, defined as an integral of the form B(x,y) = 01 t^(x-1) (1-t)^(y-1) dt, serves as a symmetric counterpart to Gamma functions and is instrumental in probability and combinatorics. The Riemann Zeta function z(s), critical in analytic number theory, is expressed by the series z(s) = n=1^ 1/n^s for complex s with real part greater than 1, linking deeply to the distribution of prime numbers. Both functions exhibit fundamental roles in complex analysis and mathematical physics, with the Beta function bridging factorials and binomial coefficients while the Zeta function encapsulates properties of prime enumerations and the behavior of L-series.
Historical Origins of the Beta and Zeta Functions
The Beta function, originally studied by Euler in the 18th century, emerged from his work on integral calculus and factorials, providing a bridge to the Gamma function through its integral representation. The Zeta function, introduced by Riemann in the 19th century as a complex function extending Euler's series, gained prominence in number theory for its deep connection to the distribution of prime numbers via the Riemann Hypothesis. Both functions have foundational roles in analysis and number theory, reflecting the evolution of mathematical understanding from Euler's classical work to Riemann's complex analysis framework.
Defining the Beta Function
The Beta function, also known as the Euler integral of the first kind, is defined as the integral from 0 to 1 of t^(x-1) * (1-t)^(y-1) dt, where x and y are complex numbers with positive real parts. It serves as a symmetric function and can be expressed using the Gamma function: B(x, y) = G(x)G(y) / G(x + y). Unlike the Riemann Zeta function, which sums infinite series related to prime distributions, the Beta function primarily appears in probability, combinatorics, and calculus through its connection to binomial coefficients and continuous distributions.
Defining the Zeta Function
The Zeta function, primarily defined as the Riemann Zeta function z(s) for complex variable s, is expressed as the infinite series z(s) = S n=1 to 1/n^s, converging for Re(s) > 1 and extended analytically elsewhere. The Beta function B(x, y), in contrast, relates to the Gamma function and is defined as an integral B(x, y) = 0^1 t^(x-1)(1-t)^(y-1) dt, which converges for Re(x) > 0 and Re(y) > 0. The Zeta function plays a crucial role in number theory and complex analysis, while the Beta function serves as a normalization constant in probability distributions and combinatorics.
Fundamental Properties: Beta vs Zeta
The Beta function, defined as B(x, y) = 01 t^{x-1}(1-t)^{y-1} dt, exhibits symmetry B(x, y) = B(y, x) and relates directly to Gamma functions via B(x, y) = G(x)G(y)/G(x+y). The Zeta function z(s), especially the Riemann Zeta function, is defined as z(s) = _{n=1}^ n^{-s} for Re(s) > 1, featuring analytic continuation and a critical strip important for prime number theory. While the Beta function focuses on integral representations and factorial relations, the Zeta function centers on infinite series, analytic continuation, and deep connections with number theory and the distribution of prime numbers.
Key Applications in Mathematics and Physics
The Beta function plays a crucial role in calculus, probability theory, and combinatorics, facilitating the evaluation of integrals involving products of powers and appearing in the study of Euler integrals and binomial coefficients. The Riemann Zeta function is fundamental in number theory for analyzing the distribution of prime numbers and has essential applications in quantum physics, particularly in statistical mechanics and quantum chaos through spectral zeta functions. Both functions serve as vital tools in complex analysis, with the Beta function closely linked to Gamma functions and the Zeta function integral to the theory of L-functions and modular forms.
Important Formulas and Relationships
The Beta function, defined as B(x,y) = 01 t^(x-1)(1-t)^(y-1) dt, is closely related to the Gamma function through B(x,y) = G(x)G(y)/G(x+y). The Riemann Zeta function, z(s) = n=1^ 1/n^s for Re(s) > 1, connects to the Beta function via integral representations and the Euler reflection formula, revealing profound links in analytic number theory. Key relationships include the Euler product formula for z(s) and the integral expressions that relate z(s) and Beta functions through the Mellin transform.
Connections to Gamma Function
The Beta function \( B(x, y) \) is directly expressed through the Gamma function by the formula \( B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \), establishing a fundamental multiplicative relationship. The Zeta function, particularly the Riemann Zeta function \( \zeta(s) \), can be connected to the Gamma function via the integral representation \( \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x - 1} \, dx \), linking analytic continuation and system behavior in number theory. Both functions leverage the Gamma function to extend their definitions to complex domains, enabling advanced applications in mathematical analysis and theoretical physics.
Analogies and Distinctions: Beta vs Zeta
The Beta function, defined as an integral involving products of powers of variables, analogously complements the Zeta function, known for its analytic continuation and connection to prime number distribution. While both functions play crucial roles in complex analysis and number theory, the Beta function primarily evaluates integrals across [0,1], relating closely to Gamma functions, whereas the Zeta function extends over infinite series and encapsulates critical zeros linked to the Riemann Hypothesis. Distinctions arise in their domain and applications, with Beta functions used extensively in probability and combinatorics, contrasted by Zeta functions dominating studies in prime asymptotics and spectral theory.
Modern Research and Future Directions
Modern research in the Beta function explores its applications in complex analysis, probability theory, and mathematical physics, emphasizing its role in evaluating integrals and special functions. The Riemann Zeta function remains central to number theory, with ongoing efforts to prove the Riemann Hypothesis, influencing prime number distribution and quantum chaos. Future directions include developing computational methods for high-precision evaluations and exploring connections between these functions in string theory and cryptography.
Beta function Infographic
 libterm.com
libterm.com