Offering a free product can significantly boost customer interest and increase brand visibility while encouraging trial and feedback. Your audience will appreciate the opportunity to experience the value of your product with no financial risk, fostering trust and loyalty. Discover how to effectively leverage free products to grow your business by reading the rest of the article.
Table of Comparison
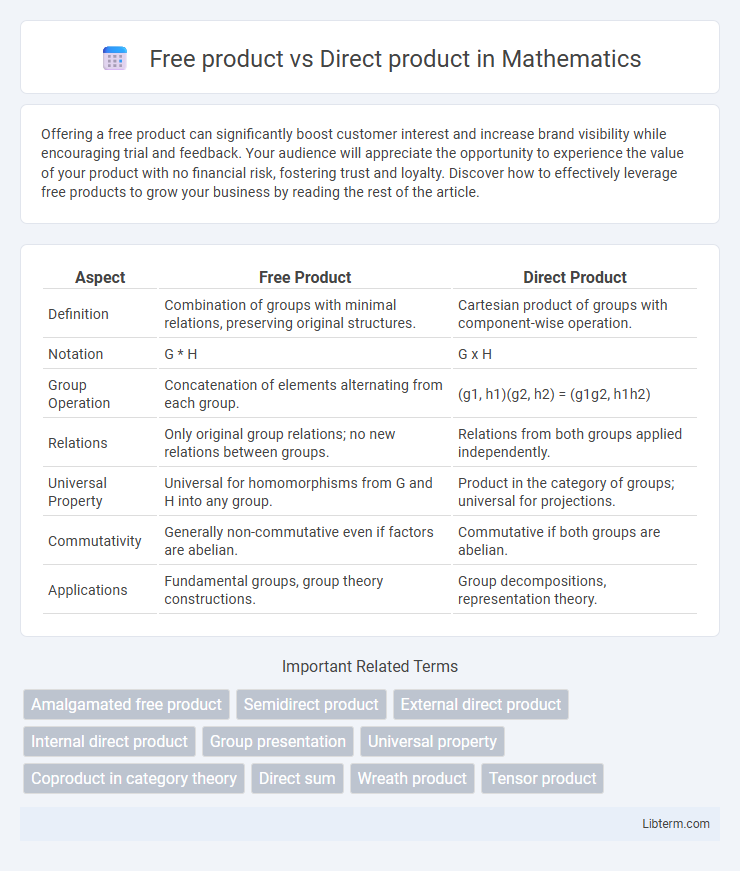
| Aspect | Free Product | Direct Product |
|---|---|---|
| Definition | Combination of groups with minimal relations, preserving original structures. | Cartesian product of groups with component-wise operation. |
| Notation | G * H | G x H |
| Group Operation | Concatenation of elements alternating from each group. | (g1, h1)(g2, h2) = (g1g2, h1h2) |
| Relations | Only original group relations; no new relations between groups. | Relations from both groups applied independently. |
| Universal Property | Universal for homomorphisms from G and H into any group. | Product in the category of groups; universal for projections. |
| Commutativity | Generally non-commutative even if factors are abelian. | Commutative if both groups are abelian. |
| Applications | Fundamental groups, group theory constructions. | Group decompositions, representation theory. |
Understanding Free Product and Direct Product
Understanding free products involves combining groups while preserving their individual structures without imposing new relations between them, resulting in a group that contains all elements of the original groups as subgroups. Direct products create a group from multiple groups by pairing elements and defining operations componentwise, effectively forming a Cartesian product with independent operation on each component. The free product emphasizes the freedom to concatenate elements from each group arbitrarily, whereas the direct product maintains strict coordinatewise operations and inter-element independence.
Key Differences Between Free and Direct Products
The free product of groups combines elements from two groups without imposing new relations, resulting in a group that contains both as subgroups with minimal interactions, while the direct product forms ordered pairs from each group's elements, imposing component-wise operations and preserving group structure independently. In free products, the elements alternate between factors and no additional relations are imposed except those in the original groups; in direct products, elements combine in a fixed coordinate-wise manner, ensuring commutativity between components when both groups are abelian. Free products are used to construct more complex groups from simpler ones without forced relations, whereas direct products are instrumental in creating product groups with predictable and independent group operations on each factor.
Algebraic Structures Involving Free and Direct Products
Free products in algebraic structures, such as groups or algebras, combine entities without imposing relations beyond those inherent in the original structures, preserving their individual identities and allowing for maximum freedom in element composition. Direct products form a new algebraic structure by pairing elements from each component, enforcing independent operations coordinate-wise and enabling decomposition into simpler substructures. Understanding the interplay between free and direct products is crucial in algebraic topology, group theory, and universal algebra for constructing complex systems from simpler building blocks.
Free Product: Definition and Core Concepts
Free product in group theory is an operation combining two or more groups into a new group, preserving the structure of each original group without imposing additional relations between them. It is defined as the coproduct in the category of groups, allowing elements from the constituent groups to alternate freely in forming group elements. This construction contrasts with the direct product by enabling nontrivial amalgamations, where the free product often leads to groups with more complex, non-abelian structures.
Direct Product: Definition and Core Concepts
Direct product refers to a mathematical operation that combines two algebraic structures, such as groups, rings, or modules, into a new structure whose elements are ordered pairs formed from the original sets. Each component in the ordered pair operates independently according to its original structure's rules, enabling the preservation of properties and facilitating complex constructions in abstract algebra. This concept plays a crucial role in various areas including group theory, topology, and category theory, where the direct product helps analyze systems by decomposing them into simpler, well-understood components.
Examples of Free Products in Group Theory
Free products in group theory combine groups such that elements from each group alternate without imposing relations beyond those in the original groups, exemplified by the free product of Z_2 and Z_3 forming an infinite group with elements alternating between orders 2 and 3. The free product of cyclic groups like Z_2 * Z_2 produces the infinite dihedral group, showcasing how free products generate complex groups from simpler cyclic components. In contrast to direct products, which impose commutativity between components, free products preserve the distinct identities of the original groups within the combined structure.
Examples of Direct Products in Group Theory
Direct products in group theory often appear in cases like the group \(\mathbb{Z}_m \times \mathbb{Z}_n\), where \(m\) and \(n\) are integers, forming a composite structure from two cyclic groups. The symmetric group \(S_3 \times \mathbb{Z}_2\) illustrates a non-abelian direct product combining permutation and cyclic elements. Unlike free products that amalgamate groups with minimal relations, direct products preserve the structure and operation within each component, enabling decompositions into subgroups such as in \(\mathbb{Z} \times \mathbb{Z}\).
Applications of Free and Direct Products in Mathematics
Free products allow the construction of complex algebraic structures by combining groups while preserving their individual identities, playing a key role in geometric group theory and topology for analyzing fundamental groups of spaces. Direct products enable the formation of new groups through the Cartesian product of existing groups, facilitating the study of group actions, representation theory, and simplifying problems in algebraic structures by breaking them into simpler, independent components. Applications of free products include decomposing spaces into simpler parts via Van Kampen's theorem, whereas direct products are essential in constructing product spaces in topology and forming product objects in category theory.
Advantages and Limitations of Each Product
Free product constructions in algebra provide flexibility by embedding factors with minimal relations, enabling universal mapping properties that aid in theoretical problem-solving and category theory applications; however, their complexity can escalate quickly, making explicit calculations and structural analysis challenging. Direct product structures simplify analysis by combining components element-wise, preserving individual factor properties and facilitating computations, yet they impose strict product relations that limit the representation of more intricate algebraic phenomena. Free products support diverse algebraic combinations, ideal for constructing new objects with specified generators, whereas direct products excel in modular decomposition but restrict interactions between components.
Choosing Between Free Product and Direct Product
Choosing between free product and direct product depends on the properties of the groups involved and the desired structure of the combined group. Free products combine groups without imposing additional relations, creating a group with elements formed by alternating sequences of elements from each group, maximizing freedom and flexibility. Direct products impose relations by pairing elements component-wise, producing a more structured and often simpler product suited for applications requiring independent subgroup actions or Cartesian product-like behavior.
Free product Infographic
 libterm.com
libterm.com