Noetherian rings form a fundamental class of rings in algebra characterized by every ascending chain of ideals stabilizing, ensuring no infinite strictly increasing sequences exist. This property simplifies the study of ring theory and module theory by guaranteeing finiteness conditions essential for various algebraic proofs and applications. Explore the rest of this article to deepen your understanding of Noetherian concepts and their crucial role in modern mathematics.
Table of Comparison
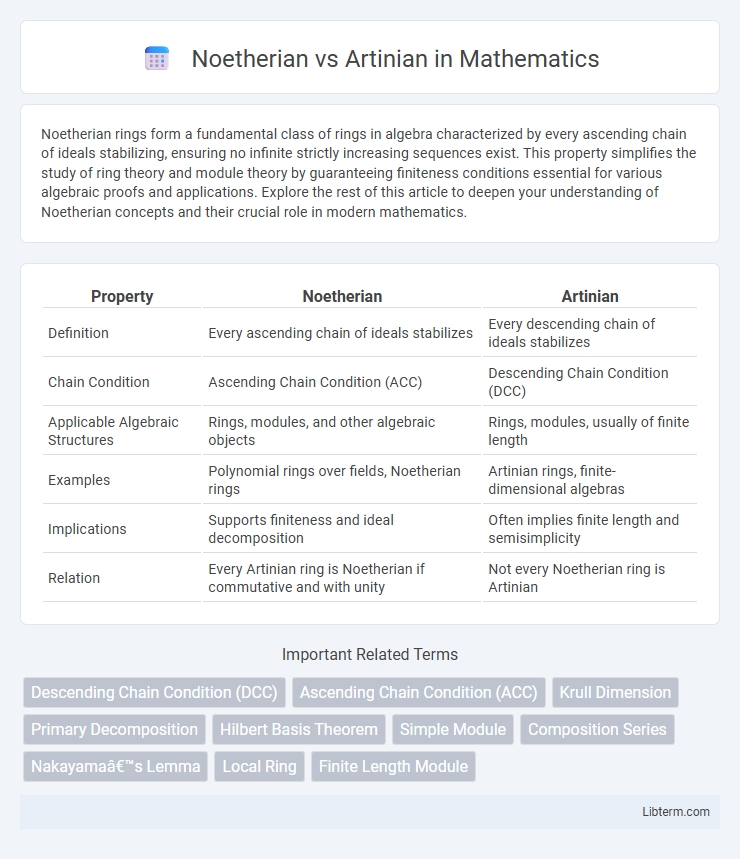
| Property | Noetherian | Artinian |
|---|---|---|
| Definition | Every ascending chain of ideals stabilizes | Every descending chain of ideals stabilizes |
| Chain Condition | Ascending Chain Condition (ACC) | Descending Chain Condition (DCC) |
| Applicable Algebraic Structures | Rings, modules, and other algebraic objects | Rings, modules, usually of finite length |
| Examples | Polynomial rings over fields, Noetherian rings | Artinian rings, finite-dimensional algebras |
| Implications | Supports finiteness and ideal decomposition | Often implies finite length and semisimplicity |
| Relation | Every Artinian ring is Noetherian if commutative and with unity | Not every Noetherian ring is Artinian |
Introduction to Noetherian and Artinian Rings
Noetherian rings are characterized by the ascending chain condition on ideals, ensuring every increasing sequence of ideals stabilizes, which guarantees that ideals are finitely generated. Artinian rings satisfy the descending chain condition on ideals, meaning every decreasing sequence of ideals eventually stabilizes, often leading to rings with finite length modules. Both classes play a fundamental role in ring theory, with Noetherian rings central to algebraic geometry and commutative algebra, while Artinian rings are crucial in the study of module decomposition and representation theory.
Fundamental Definitions: Noetherian vs Artinian Structures
Noetherian structures are defined by the ascending chain condition, ensuring every increasing sequence of submodules or ideals stabilizes, which guarantees the existence of maximal elements and finite generation properties. Artinian structures satisfy the descending chain condition, where every decreasing sequence of submodules or ideals eventually stabilizes, emphasizing minimal elements and often linked to finite length conditions. Both concepts play critical roles in ring theory and module theory, distinguishing types of finiteness conditions that influence decomposition and classification theorems.
Historical Background and Significance
Noetherian and Artinian conditions originated from the work of Emmy Noether and Emil Artin in the early 20th century, profoundly shaping ring theory and module theory. Noether introduced the ascending chain condition to address infinite ideal chains, enabling a systematic classification of algebraic structures, while Artin developed the descending chain condition to study finite conditions on modules. These foundational concepts remain central in modern algebra, impacting algebraic geometry, representation theory, and homological algebra by controlling structural complexity and ensuring finiteness properties.
Key Properties and Characterizations
Noetherian rings are characterized by the ascending chain condition on ideals, ensuring every increasing sequence of ideals stabilizes, which guarantees the existence of maximal elements and finite generation properties. Artinian rings satisfy the descending chain condition on ideals, implying that every decreasing sequence of ideals terminates and such rings are always Noetherian with finite length modules. Key distinctions include the fact that Noetherian rings ensure control over ideal growth while Artinian rings emphasize ideal stabilization from above, with Artinian rings often decomposable into a finite direct product of local Artin rings.
Examples of Noetherian and Artinian Rings
Noetherian rings include well-known examples such as polynomial rings over fields like k[x], where k is a field, and the ring of integers Z, both of which satisfy the ascending chain condition on ideals. Artinian rings often arise as finite-dimensional algebras over a field, for instance, matrix rings M_n(k) over a field k or quotient rings like k[x]/(x^n), which satisfy the descending chain condition on ideals. These examples highlight the distinction that Noetherian rings control ascending chains of ideals, while Artinian rings control descending chains, with many Artinian rings also being Noetherian but not vice versa.
Chain Conditions: ASC vs DSC
Noetherian rings satisfy the Ascending Chain Condition (ACC), ensuring every ascending chain of ideals stabilizes, which guarantees finiteness properties crucial in algebraic geometry and module theory. Artinian rings, conversely, obey the Descending Chain Condition (DCC), meaning every descending chain of ideals stabilizes, often characterizing finite-dimensional algebras over a field. The ACC and DCC conditions fundamentally distinguish the structural behavior of Noetherian and Artinian rings, impacting their ideal decomposition and module classification.
Noetherian Modules vs Artinian Modules
Noetherian modules satisfy the ascending chain condition on submodules, ensuring every increasing sequence stabilizes, which guarantees the module is finitely generated in many important cases. Artinian modules, conversely, fulfill the descending chain condition, meaning every decreasing sequence of submodules stabilizes, often leading to finiteness properties that reflect a form of minimality. The distinction emphasizes that Noetherian modules are controlled by growth constraints, while Artinian modules are characterized by constraints on descending complexity within module structure.
Interrelationships and Contrasts
Noetherian and Artinian conditions both characterize finiteness properties in ring and module theory, but differ fundamentally in their chain conditions: Noetherian rings satisfy the ascending chain condition on ideals, whereas Artinian rings satisfy the descending chain condition. Every Artinian ring is necessarily Noetherian, reflecting a strict inclusion in the class of rings, but the converse is false as Noetherian rings need not be Artinian. These contrasting chain conditions provide key insights into module decompositions, structure theorems, and representation theory in algebra.
Applications in Algebra and Geometry
Noetherian rings and modules are fundamental in algebraic geometry for ensuring the finiteness conditions necessary for the Hilbert basis theorem, which guarantees the stability of ideal generation and enables the classification of algebraic varieties. Artinian rings primarily appear in representation theory and algebraic geometry through their role in analyzing local properties of schemes and modules via Artinian local rings, facilitating the study of zero-dimensional schemes and singularities. The interplay between Noetherian and Artinian conditions underpins key concepts such as dimension theory, module decomposition, and cohomological finiteness properties in both algebra and geometry.
Conclusion and Further Reading
Noetherian rings ensure ascending chain conditions while Artinian rings satisfy descending chain conditions, both crucial in module theory and algebraic geometry. For deeper insights, explore texts like "Introduction to Commutative Algebra" by Atiyah and MacDonald, and Matsumura's "Commutative Ring Theory" for advanced treatments. Research articles on ring theory and module classification offer extensive case studies and applications beyond foundational concepts.
Noetherian Infographic
 libterm.com
libterm.com