Colimits are fundamental constructions in category theory that generalize the concept of combining objects and morphisms. They capture the notion of the most efficient way to coalesce a diagram of objects into a single universal object, encompassing coproducts, pushouts, and direct limits. Explore the rest of this article to understand how colimits structure mathematical and computational frameworks essential for your studies.
Table of Comparison
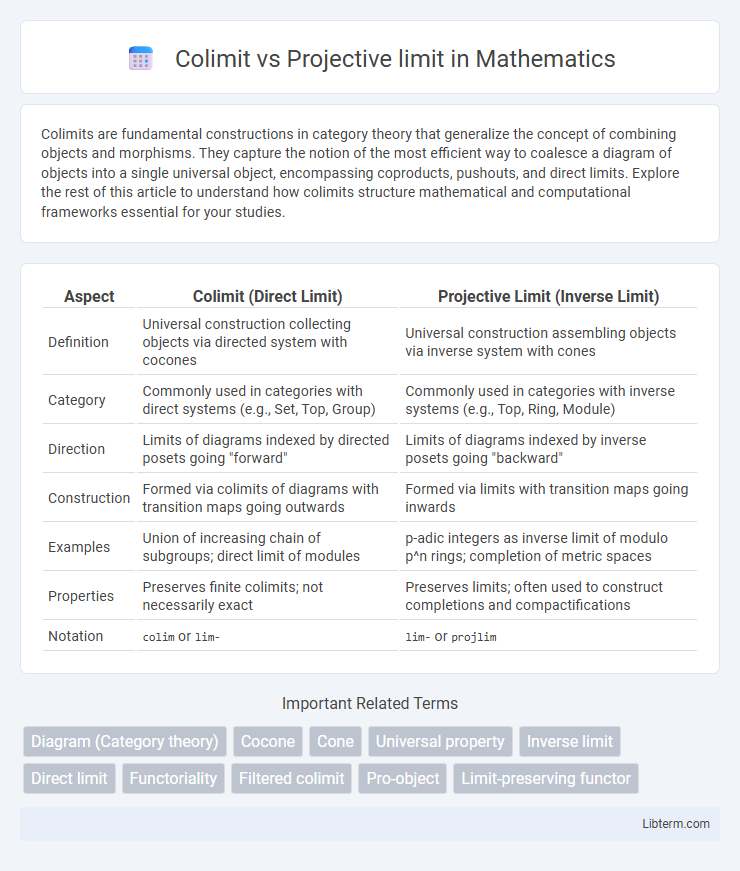
| Aspect | Colimit (Direct Limit) | Projective Limit (Inverse Limit) |
|---|---|---|
| Definition | Universal construction collecting objects via directed system with cocones | Universal construction assembling objects via inverse system with cones |
| Category | Commonly used in categories with direct systems (e.g., Set, Top, Group) | Commonly used in categories with inverse systems (e.g., Top, Ring, Module) |
| Direction | Limits of diagrams indexed by directed posets going "forward" | Limits of diagrams indexed by inverse posets going "backward" |
| Construction | Formed via colimits of diagrams with transition maps going outwards | Formed via limits with transition maps going inwards |
| Examples | Union of increasing chain of subgroups; direct limit of modules | p-adic integers as inverse limit of modulo p^n rings; completion of metric spaces |
| Properties | Preserves finite colimits; not necessarily exact | Preserves limits; often used to construct completions and compactifications |
| Notation | colim or lim- |
lim- or projlim |
Introduction to Colimits and Projective Limits
Colimits and projective limits are fundamental constructions in category theory used to generalize notions of unions and intersections. Colimits, also known as inductive limits, represent the most general object coalescing a diagram of objects via universal cocones, capturing ways to coherently combine structures. Projective limits, or inverse limits, provide an object receiving compatible morphisms from a diagram, embodying a universal cone that encodes consistent descent data across the system.
Fundamental Concepts in Category Theory
Colimits and projective limits represent dual constructions in category theory, where colimits generalize the notion of a universal cocone and capture the essence of "gluing" objects along morphisms, while projective limits (also known as inverse limits) involve universal cones that allow consistent factorization through a diagram of objects. Fundamental concepts include the use of diagrams indexed by directed categories, the preservation of limits or colimits by functors, and the role of universal properties in defining these limits as unique up-to-isomorphism objects. Understanding the duality between colimits and projective limits clarifies their applications in topology, algebra, and computer science, reflecting how complex structures are assembled or decomposed in categorical frameworks.
Defining Colimit: Meaning and Examples
A colimit in category theory represents the most general object that coherently summarizes a diagram of objects and morphisms, capturing the essence of "gluing" or "coalescing" structures along shared parts. It generalizes constructions like coproducts, pushouts, and direct limits, providing a universal cocone under a diagram. For example, in the category of sets, the colimit of a diagram of sets and functions is their disjoint union modulo an equivalence relation imposed by the morphisms.
Projective Limit Explained: Key Ideas and Instances
Projective limits, also known as inverse limits, are constructions in category theory that assemble a system of spaces or objects indexed by a directed set with morphisms going "backward." They capture the idea of coherently gluing together compatible elements from a family of objects, producing a universal object equipped with projections to each component. Common instances include the p-adic integers as the projective limit of the inverse system of rings Z/p^nZ and the inverse limit of topological spaces, which preserves properties like compactness or completeness under suitable conditions.
Differences Between Colimit and Projective Limit
Colimits and projective limits differ fundamentally in their directionality and construction within category theory: colimits are universal constructions that amalgamate diagrams by cocones from below, while projective limits (inverse limits) arise from cones pointing into the diagram from above. Colimits correspond to categorical sums or unions, preserving colimits of diagrams indexed by filtered categories, whereas projective limits generalize intersections or products, preserving limits over cofiltered indexing categories. The distinction emphasizes colimits' role in synthesizing objects through coprojections versus projective limits capturing coherent consistency conditions via projections.
Visualizing Colimit and Projective Limit Diagrams
Colimit diagrams can be visualized as a universal construction that unifies objects and morphisms by merging or identifying parts in a cocone structure, often resembling a "co-span" where multiple objects map into a single colimit object. Projective limit diagrams visualize a universal object mapping consistently to a family of objects, forming a cone where all morphisms commute backward along a directed system. Diagrammatic representations highlight the dual nature: colimits focus on the outgoing morphisms converging to a universal cocone, while projective limits emphasize incoming morphisms forming a universal cone preserving compatibility across the diagram.
Applications of Colimits vs Projective Limits
Colimits are widely used in algebraic topology and category theory for constructing objects by "gluing" smaller pieces together, such as in the formation of quotient spaces and pushouts. Projective limits, or inverse limits, find applications in algebraic geometry and number theory, particularly in studying profinite groups, towers of field extensions, and completing structures via limits of finite approximations. Both concepts are essential in handling infinite constructions, with colimits focusing on assembling and projective limits focusing on approximating or extracting consistent systems.
Properties and Universal Constructions
Colimits generalize constructions like coproducts and pushouts, characterized by a universal property that every cocone from the diagram factors uniquely through the colimit. Projective limits, or inverse limits, represent limits of diagrams by combining objects in a way that respects transition morphisms, satisfying a universal property ensuring unique factorization of cones into the limit. Both serve as universal constructions in category theory, with colimits capturing the notion of "gluing" objects together and projective limits encoding consistent "projections" compatible with the diagram structure.
Common Contexts: Algebra, Topology, and Beyond
Colimits and projective limits serve dual roles in algebra and topology, where colimits often model constructions such as quotients, direct sums, and unions, while projective limits capture inverse systems like inverse limits of groups, rings, or topological spaces. In algebra, colimits unify directed systems of modules or algebras by forming objects that preserve structure under morphisms, whereas projective limits assemble objects like profinite groups via compatible projections. Beyond these areas, colimits and projective limits provide frameworks for gluing data and analyzing limiting behaviors in categories such as sheaves, homotopy theory, and functional analysis.
Summary: Choosing Between Colimit and Projective Limit
Colimits and projective limits serve distinct purposes in category theory, where colimits generalize constructions like unions and direct limits, while projective limits generalize intersections and inverse limits. Selecting between a colimit and a projective limit depends on whether the objective is to combine data structures along morphisms (colimit) or to extract compatible data across a system of objects (projective limit). The choice influences the preservation of properties such as exactness, continuity, or compactness in algebraic topology, algebraic geometry, and related fields.
Colimit Infographic
 libterm.com
libterm.com