Lambda calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application. It serves as the foundation for functional programming languages and helps in understanding how functions operate and interact. Explore the rest of this article to discover how lambda calculus can deepen your understanding of programming paradigms and computational theory.
Table of Comparison
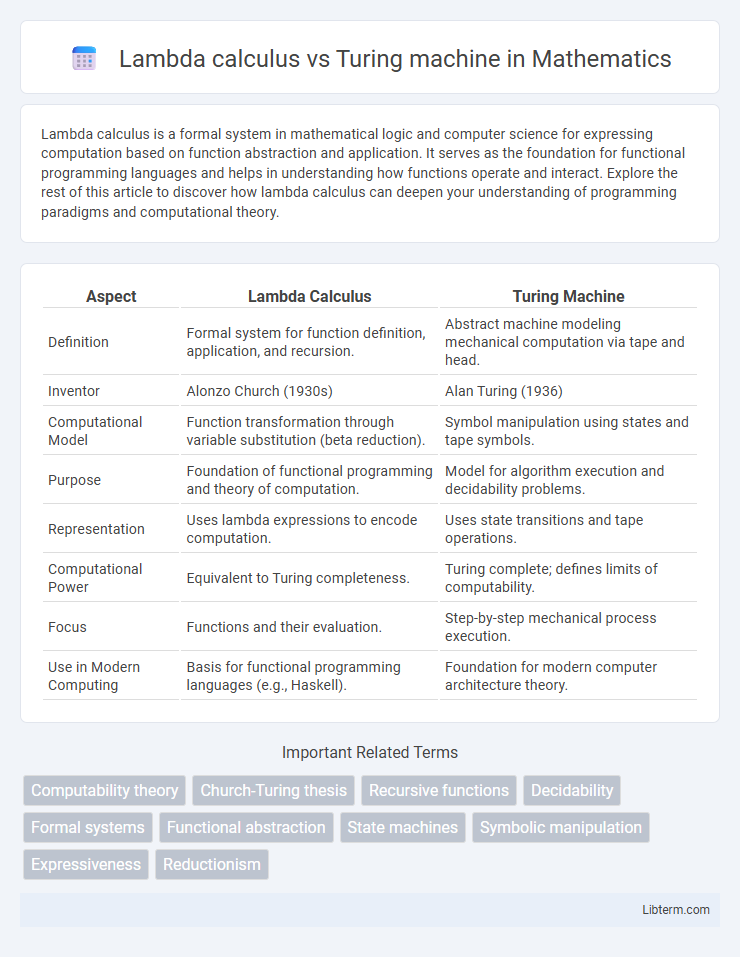
| Aspect | Lambda Calculus | Turing Machine |
|---|---|---|
| Definition | Formal system for function definition, application, and recursion. | Abstract machine modeling mechanical computation via tape and head. |
| Inventor | Alonzo Church (1930s) | Alan Turing (1936) |
| Computational Model | Function transformation through variable substitution (beta reduction). | Symbol manipulation using states and tape symbols. |
| Purpose | Foundation of functional programming and theory of computation. | Model for algorithm execution and decidability problems. |
| Representation | Uses lambda expressions to encode computation. | Uses state transitions and tape operations. |
| Computational Power | Equivalent to Turing completeness. | Turing complete; defines limits of computability. |
| Focus | Functions and their evaluation. | Step-by-step mechanical process execution. |
| Use in Modern Computing | Basis for functional programming languages (e.g., Haskell). | Foundation for modern computer architecture theory. |
Introduction to Lambda Calculus and Turing Machines
Lambda calculus, developed by Alonzo Church in the 1930s, is a formal system in mathematical logic for expressing computation through function abstraction and application, forming the foundation of functional programming languages. Turing machines, introduced by Alan Turing, are abstract computational models that manipulate symbols on an infinite tape according to a set of rules, serving as a fundamental concept in automata theory and computability. Both frameworks are equivalent in computational power, providing different perspectives on algorithms and the limits of computation.
Historical Background and Development
Lambda calculus, developed by Alonzo Church in the 1930s, served as a formal system for expressing computation based on function abstraction and application. Alan Turing independently formulated the concept of Turing machines around the same time, providing a mechanical model of computation aimed at formalizing algorithms and decidability. Both frameworks laid foundational groundwork for modern computer science by addressing the limits of computation and enabling the formal analysis of algorithms.
Formal Definitions and Syntax
Lambda calculus is defined through formal rules involving variables, function abstraction, and application, using a simple syntax of expressions composed of variables, l-abstractions (lx.E), and applications (E1 E2). In contrast, Turing machines are formally described by a 7-tuple consisting of a finite set of states, an input alphabet, a tape alphabet, a transition function, a start state, a blank symbol, and a set of accept states, with syntax represented through transition rules guiding state changes and tape manipulations. Both serve as foundational models of computation, with lambda calculus focusing on symbolic function manipulation and Turing machines emphasizing state-driven mechanical processes.
Computation Models: How They Work
Lambda calculus represents computation through function abstraction and application, manipulating symbolic expressions to perform calculations without a machine state. In contrast, Turing machines operate by reading and writing symbols on an infinite tape using a finite set of states and transition rules to simulate algorithmic processes. Both models capture the essence of computation, with lambda calculus emphasizing function transformations and Turing machines modeling mechanical step-by-step operations.
Expressiveness and Computational Power
Lambda calculus and Turing machines possess equivalent computational power, both capable of expressing any computable function as defined by Church-Turing thesis. Lambda calculus emphasizes function abstraction and application through variable binding, making it a foundational model in functional programming and formal logic. Turing machines provide a more operational perspective by simulating algorithms with states and tape manipulation, often used to analyze algorithmic complexity and decidability.
Equivalence: Church-Turing Thesis
Lambda calculus and Turing machines are both computational models that define what can be algorithmically computed, forming the foundation of modern computability theory. The Church-Turing Thesis asserts their equivalence by stating that any function computable by a Turing machine can also be computed using lambda calculus, and vice versa. This equivalence highlights their role in formalizing the concept of effective computation and underpins much of theoretical computer science.
Examples of Computations in Both Models
Lambda calculus expresses computations through function abstraction and application, such as defining the identity function lx.x or performing Church numerals addition like (lm.ln.lf.lx.m f (n f x)). Turing machines manipulate symbols on a tape using state transitions, exemplified by a machine that increments a unary number by moving right to find the end of the sequence and appending a symbol. Both models can simulate any computable function, illustrating their equivalence in representing computation despite their differing operational frameworks.
Advantages and Limitations
Lambda calculus offers a simple yet powerful formal system for expressing computation using function abstraction and application, making it ideal for understanding functional programming languages and enabling proofs about program behavior. However, its abstraction level can be challenging for modeling low-level machine operations and hardware implementation details. Turing machines provide a more concrete model of computation through state transitions and tape manipulation, making them better suited for simulating algorithms step-by-step and analyzing computational complexity, though their mechanical nature is less expressive for high-level symbolic transformations.
Real-World Applications and Influence
Lambda calculus underpins the foundations of functional programming languages such as Haskell and Lisp, influencing compiler design and automated theorem proving through its treatment of functions as first-class objects. Turing machines provide the theoretical framework for understanding computability and complexity, guiding the development of algorithms and computational limits in fields like cryptography and artificial intelligence. Both models drive advancements in modern computer science by shaping programming paradigms and informing the boundaries of machine computation.
Conclusion: Choosing Between Lambda Calculus and Turing Machines
Selecting between Lambda Calculus and Turing Machines hinges on the context of computational theory and practical application. Lambda Calculus excels in expressing functions and higher-order abstractions, making it ideal for functional programming language design and formal reasoning about computation. Turing Machines provide a clearer framework for modeling algorithmic processes and decidability, serving as a foundation for complexity theory and automata analysis.
Lambda calculus Infographic
 libterm.com
libterm.com