A Bernstein set is a subset of the real numbers with unique topological properties: it intersects every uncountable closed set but contains no perfect subset itself. This concept highlights intriguing aspects of set theory and measure theory, revealing how non-measurable sets defy intuition. Explore the rest of the article to understand how Bernstein sets challenge conventional ideas in mathematics.
Table of Comparison
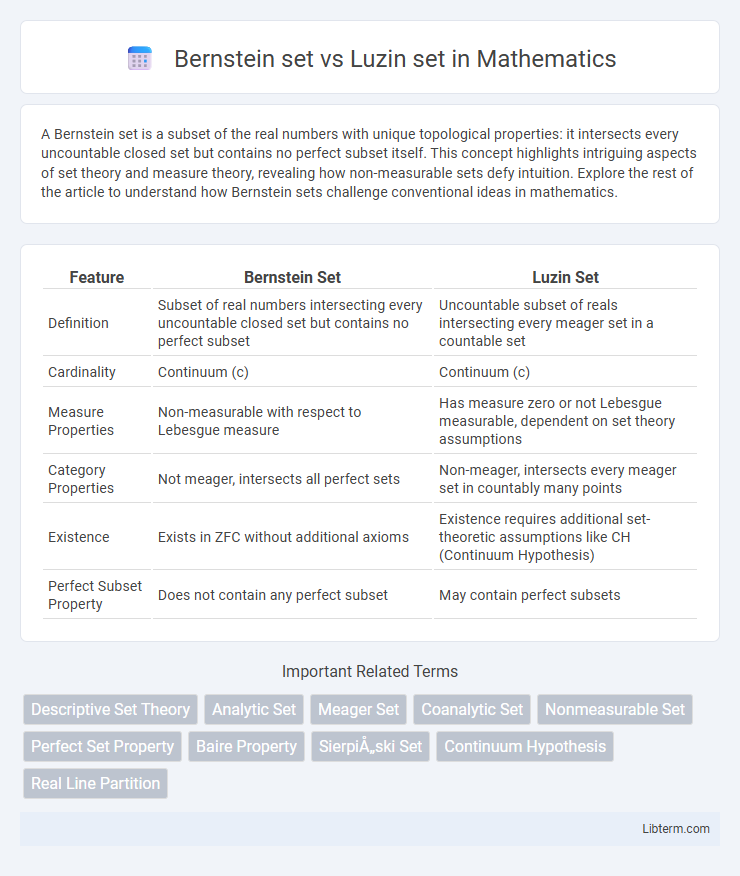
| Feature | Bernstein Set | Luzin Set |
|---|---|---|
| Definition | Subset of real numbers intersecting every uncountable closed set but contains no perfect subset | Uncountable subset of reals intersecting every meager set in a countable set |
| Cardinality | Continuum (c) | Continuum (c) |
| Measure Properties | Non-measurable with respect to Lebesgue measure | Has measure zero or not Lebesgue measurable, dependent on set theory assumptions |
| Category Properties | Not meager, intersects all perfect sets | Non-meager, intersects every meager set in countably many points |
| Existence | Exists in ZFC without additional axioms | Existence requires additional set-theoretic assumptions like CH (Continuum Hypothesis) |
| Perfect Subset Property | Does not contain any perfect subset | May contain perfect subsets |
Introduction to Bernstein and Luzin Sets
Bernstein sets are subsets of the real numbers characterized by intersecting every uncountable closed set without containing any uncountable closed subset themselves, highlighting their intricate measure-theoretic properties. Luzin sets are uncountable subsets of the real line with the property that every meager set intersects them in only countably many points, emphasizing their role in category theory and descriptive set theory. Both sets serve as essential examples in real analysis and set theory, illustrating the complexity of measurable and category-related structures.
Historical Background and Motivation
Bernstein sets and Luzin sets emerged in the early 20th century during the development of descriptive set theory and measure theory, reflecting efforts to understand pathological subsets of real numbers. Felix Bernstein introduced Bernstein sets to demonstrate subsets that intersect every uncountable closed set but contain no perfect subset, challenging classical notions of measure and category. Nikolai Luzin motivated the concept of Luzin sets to exhibit uncountable sets with countable intersections with any meager set, highlighting subtle properties in the topology of the real line related to the axiom of choice and measure zero sets.
Definition of Bernstein Set
A Bernstein set is a subset of the real numbers constructed so that it intersects every uncountable closed subset of the real line but contains no perfect subset itself, making it non-measurable and having no Borel or Lebesgue measurable structure. In contrast, a Luzin set is an uncountable subset of the real numbers where every countable subset is nowhere dense, ensuring that its intersection with any meager set is countable. Both sets illustrate different pathological examples in descriptive set theory, challenging classical notions of size and measurability.
Definition of Luzin Set
A Luzin set is an uncountable subset of the real numbers where every meager set intersects the Luzin set in only countably many points, illustrating its strong anti-meager property. In contrast, a Bernstein set intersects every uncountable closed set but contains no perfect subsets, highlighting a different form of pathological set. The Luzin set's definition emphasizes its delicate balance between largeness and topological smallness, crucial in descriptive set theory and real analysis.
Set-Theoretic Properties and Cardinality
Bernstein sets and Luzin sets both arise in descriptive set theory, exhibiting unique set-theoretic properties linked to the real line. A Bernstein set is uncountable, non-measurable, and intersects every uncountable closed set, preventing it from containing any perfect subset, hence having cardinality equal to the continuum (2^0). Luzin sets are also uncountable, of cardinality continuum, but are characterized by having countable intersections with every meager set, making them strong examples of sets with strong measure-theoretic and category-theoretic rarity.
Differences Between Bernstein and Luzin Sets
Bernstein sets are uncountable subsets of real numbers intersecting every uncountable closed set but containing no perfect subsets, while Luzin sets are uncountable subsets of real numbers intersecting every meager set in only countably many points. Bernstein sets are constructed using the axiom of choice to avoid perfect sets entirely, contrasting with Luzin sets that rely on category-theoretic properties to remain almost disjoint from meager sets. The key difference lies in their intersection behavior: Bernstein sets intersect all perfect sets nontrivially, whereas Luzin sets have minimal intersection with "small" sets in the sense of category.
Construction Methods for Bernstein Sets
Bernstein sets are constructed using transfinite induction, ensuring each uncountable closed set is intersected but not contained, relying heavily on the axiom of choice to select points outside all perfect subsets. This method contrasts with Luzin sets, which are constructed by enumerating the real numbers and carefully choosing points to form an uncountable set intersecting every meager set in countably many points. The Bernstein construction exploits the structure of perfect subsets in the real line, while Luzin sets focus on measure and category properties.
Construction Methods for Luzin Sets
Luzin sets are constructed using transfinite induction under the Continuum Hypothesis, allowing the selection of a subset of the real line with cardinality continuum while intersecting every meager set in only countably many points. This method ensures the Luzin set is uncountable yet remains "small" in terms of category, contrasting with Bernstein sets, which are designed to intersect every uncountable closed set without containment. The delicate construction of Luzin sets relies on iteratively avoiding meager sets to maintain their defining topological properties.
Applications in Descriptive Set Theory
Bernstein sets and Luzin sets play crucial roles in descriptive set theory by illustrating the boundaries of measurability and category. Bernstein sets, which intersect every uncountable closed set but contain no perfect subset, serve as counterexamples in the study of projective sets and demonstrate the limitations of Borel hierarchy classifications. Luzin sets, uncountable subsets of the real line where every meager set intersects them in only countably many points, are instrumental in exploring the interplay between measure and category, influencing advanced results on uniformization and definable selection principles.
Open Problems and Research Directions
Bernstein sets and Luzin sets remain central in descriptive set theory, with open problems focusing on their interactions with large cardinal axioms and determinacy hypotheses. Key research directions explore the consistency of their existence under various models of set theory, particularly regarding their measure and category properties. Investigations aim to characterize the sets in terms of definability, complexity, and their role in the structure of the real line.
Bernstein set Infographic
 libterm.com
libterm.com