A metric space is a set equipped with a distance function, known as a metric, that defines the distance between any two points in the set. This structure allows for the formal study of concepts like convergence, continuity, and compactness, which are fundamental in analysis and topology. Explore the rest of this article to deepen your understanding of how metric spaces shape various mathematical theories.
Table of Comparison
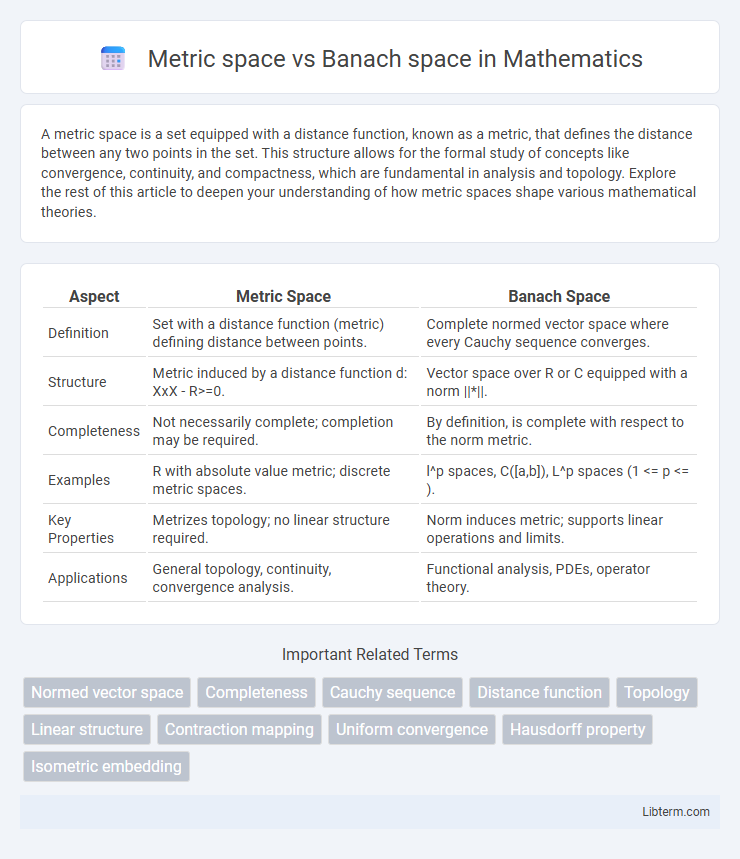
| Aspect | Metric Space | Banach Space |
|---|---|---|
| Definition | Set with a distance function (metric) defining distance between points. | Complete normed vector space where every Cauchy sequence converges. |
| Structure | Metric induced by a distance function d: XxX - R>=0. | Vector space over R or C equipped with a norm ||*||. |
| Completeness | Not necessarily complete; completion may be required. | By definition, is complete with respect to the norm metric. |
| Examples | R with absolute value metric; discrete metric spaces. | l^p spaces, C([a,b]), L^p spaces (1 <= p <= ). |
| Key Properties | Metrizes topology; no linear structure required. | Norm induces metric; supports linear operations and limits. |
| Applications | General topology, continuity, convergence analysis. | Functional analysis, PDEs, operator theory. |
Introduction to Metric Spaces
Metric spaces provide a foundational framework in mathematics by defining a set equipped with a distance function that measures the separation between any two points, enabling the analysis of convergence, continuity, and compactness. Banach spaces extend this concept by introducing a complete normed vector space, ensuring every Cauchy sequence converges within the space, which is crucial for functional analysis and solving differential equations. Understanding metric spaces is essential for grasping Banach spaces since the norm induces a metric, bridging abstract vector spaces with geometric intuition.
Fundamental Properties of Metric Spaces
Metric spaces provide the foundational structure defined by a distance function that satisfies positivity, symmetry, and the triangle inequality. Unlike Banach spaces, which are complete normed vector spaces allowing for limits of Cauchy sequences, metric spaces do not require linearity or completeness. The fundamental properties of metric spaces include open and closed sets, convergence, and continuity, which underpin more advanced concepts in functional analysis.
Understanding Banach Spaces
Banach spaces are complete normed vector spaces where every Cauchy sequence converges within the space, extending the concept of metric spaces by incorporating both vector space structure and norm-induced distance. Unlike general metric spaces that only require a distance function satisfying specific axioms, Banach spaces provide a framework for analyzing convergence, continuity, and linear operators in infinite-dimensional settings. The completeness property of Banach spaces is crucial for functional analysis, enabling rigorous treatment of function limits and stability in solving differential and integral equations.
Key Differences Between Metric and Banach Spaces
Metric spaces are general structures defined by a distance function (metric) that satisfies positivity, symmetry, and the triangle inequality, but do not require completeness or linear structure. Banach spaces are complete normed vector spaces where the norm induces a metric, ensuring every Cauchy sequence converges within the space. The key difference lies in completeness and vector space properties; every Banach space is a metric space, but not every metric space is a Banach space.
Completeness in Metric vs Banach Spaces
Completeness in metric spaces ensures every Cauchy sequence converges to a limit within the space, defining a complete metric space. Banach spaces are specific complete normed vector spaces where the norm induces the metric, guaranteeing completeness concerning both the metric and vector space structure. This completeness property in Banach spaces is fundamental for functional analysis, enabling analysis of infinite-dimensional vector spaces with a robust notion of convergence.
Examples of Metric and Banach Spaces
The set of real numbers with the usual absolute value distance is a fundamental example of a metric space, while the space of continuous functions on a closed interval with the supremum norm forms a classic Banach space. Euclidean spaces equipped with the standard distance metric illustrate metric spaces, whereas sequence spaces like \( \ell^p \) for \( p \geq 1 \) serve as important Banach space examples. Every Banach space is inherently a complete normed vector space, making it a metric space with additional structure and completeness properties.
Importance of Norms in Banach Spaces
Norms play a crucial role in Banach spaces by providing a measure of vector length and enabling the definition of convergence, continuity, and boundedness. Unlike general metric spaces, Banach spaces require completeness with respect to the norm-induced metric, ensuring the limit of every Cauchy sequence exists within the space. This structure underpins many functional analysis applications, including solving differential equations and optimization problems.
Topological Aspects: Open and Closed Sets
In metric spaces, open sets are defined using open balls determined by the metric, providing a natural topology that generalizes distance concepts. Banach spaces, being complete normed vector spaces, inherit a metric from their norm, ensuring all Cauchy sequences converge within the space, which is a key topological property. Closed sets in Banach spaces are particularly significant because the completeness guarantees that these sets contain all their limit points, making them pivotal in functional analysis and related topological studies.
Applications of Metric and Banach Spaces
Metric spaces provide the foundational framework for analyzing convergence, continuity, and compactness in various fields such as topology, computer science, and geometry. Banach spaces, being complete normed vector spaces, are essential in functional analysis and are widely applied in solving differential and integral equations, optimization problems, and signal processing. Their completeness property enables rigorous handling of infinite-dimensional vector spaces, crucial for quantum mechanics and numerical analysis.
Summary: Choosing Between Metric and Banach Spaces
Metric spaces provide a general framework characterized by a distance function satisfying positivity, symmetry, and the triangle inequality, suitable for analyzing convergence and continuity in varied contexts. Banach spaces, as complete normed vector spaces, offer powerful tools for functional analysis, enabling the use of fixed-point theorems and ensuring limits of Cauchy sequences exist within the space. Selecting between metric and Banach spaces depends on the need for vector space structure and completeness, with Banach spaces favored in problems requiring linearity and guaranteed convergence.
Metric space Infographic
 libterm.com
libterm.com