Complete knowledge of the topic empowers you to make informed decisions and enhances your understanding. Mastery of key concepts ensures clarity and effective communication in complex situations. Explore the rest of the article to deepen your insight and unlock practical applications.
Table of Comparison
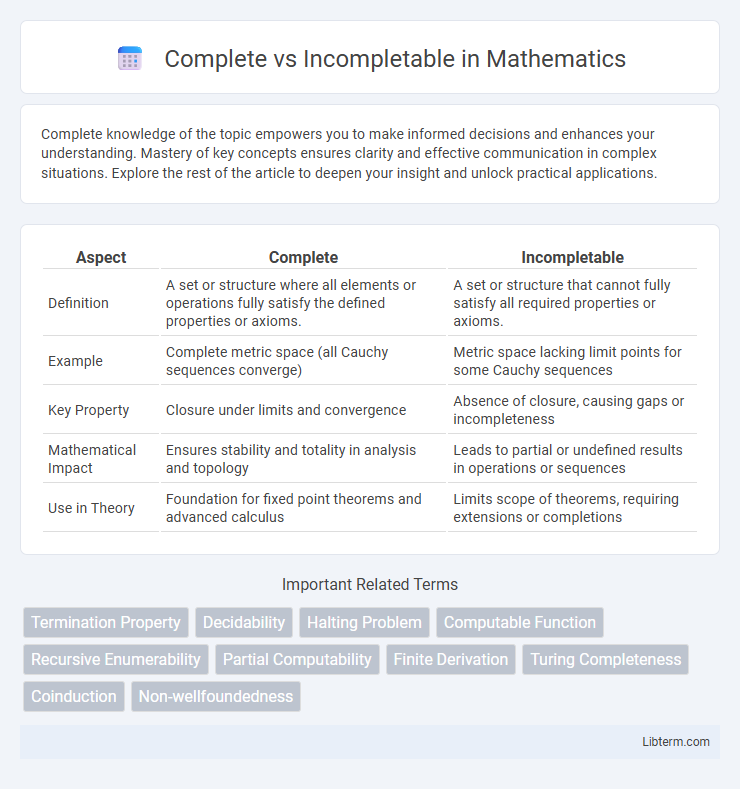
| Aspect | Complete | Incompletable |
|---|---|---|
| Definition | A set or structure where all elements or operations fully satisfy the defined properties or axioms. | A set or structure that cannot fully satisfy all required properties or axioms. |
| Example | Complete metric space (all Cauchy sequences converge) | Metric space lacking limit points for some Cauchy sequences |
| Key Property | Closure under limits and convergence | Absence of closure, causing gaps or incompleteness |
| Mathematical Impact | Ensures stability and totality in analysis and topology | Leads to partial or undefined results in operations or sequences |
| Use in Theory | Foundation for fixed point theorems and advanced calculus | Limits scope of theorems, requiring extensions or completions |
Introduction to Complete vs Incompletable
Complete tasks are those that can be fully finished within a defined scope and timeframe, meeting all specified requirements. Incompletable tasks, by contrast, lack the necessary conditions or resources to reach a definitive end, often due to external constraints or ambiguous objectives. Understanding the distinction between complete and incompletable tasks is crucial for effective project management and strategic planning.
Defining Completeness and Incompleteness
Completeness denotes a condition where all necessary elements or criteria are fully satisfied, ensuring the task or concept can be wholly realized or achieved. Incompleteness refers to scenarios where critical components, information, or steps are missing or unattainable, preventing the full realization or completion of the process. The distinction between complete and incompletable hinges on the presence or absence of all essential parts required for finality.
Historical Context and Theoretical Background
The distinction between complete and incompletable tasks originates from classical logic and computability theory, where a complete problem is one that can be fully resolved by a given algorithm, while incompletable tasks lack effective solutions within formal systems. Alan Turing's work on decidability and the Halting Problem established foundational limits, demonstrating that certain problems are inherently incompletable due to undecidability. In historical context, this theoretical framework has shaped modern computational complexity theory and influenced the classification of problems in recursive function theory and algorithm design.
Key Differences Between Complete and Incompletable
Complete tasks are fully achievable with all necessary resources and conditions met, allowing successful fulfillment. Incompletable tasks lack essential components or face insurmountable constraints, preventing their realization. The key difference lies in the feasibility and availability of means to reach the intended goal.
Common Examples in Mathematics and Logic
Complete mathematical structures contain all necessary elements or conditions to satisfy a given property, such as complete metric spaces where every Cauchy sequence converges within the space. Incompletable systems lack elements needed to meet completeness criteria, exemplified by partial orders without least upper bounds for certain subsets. Logical frameworks like complete theories ensure decidability of all statements, whereas incomplete theories have undecidable propositions, highlighting the distinction in formal logic.
Practical Applications in Computer Science
Complete problems in computer science, such as NP-complete problems, have well-defined criteria allowing an algorithm to verify solutions efficiently, facilitating practical applications in optimization, cryptography, and automated reasoning. Incompletable problems lack definitive algorithms to verify or solve all instances, impacting areas like undecidable problems in formal verification and program synthesis where no general solution exists. Understanding the distinction guides the design of algorithms and informs computational feasibility in software development and complexity theory.
Challenges of Incompletable Systems
Incompletable systems face significant challenges such as unpredictable behavior due to unresolved dependencies and partial functionality that hinders full system integration. These systems often struggle with error handling and recovery, leading to reduced reliability and increased maintenance costs. The complexity of managing incomplete data paths complicates debugging and decreases overall system performance.
Benefits of Complete Systems
Complete systems offer comprehensive functionality, ensuring all components work seamlessly to deliver full performance and user satisfaction. This integration reduces errors and maintenance costs by providing predictable, reliable outputs and facilitating streamlined workflows. Benefits include enhanced efficiency, improved user experience, and greater scalability compared to incompletable systems lacking full feature sets or interoperability.
Choosing Between Complete and Incompletable Approaches
Choosing between complete and incompletable approaches hinges on project scope and resource availability; complete methods aim for fully finished outcomes while incompletable techniques accept partial progress or iterative results. Complete approaches suit tasks demanding total fulfillment, such as regulatory compliance or final product delivery, whereas incompletable methods benefit ongoing development or research phases with evolving objectives. Evaluating deadlines, cost constraints, and flexibility requirements guides optimal selection to balance thoroughness against adaptability.
Future Developments and Emerging Trends
Future developments in distinguishing complete versus incompletable tasks emphasize advancements in AI-driven predictive analytics, enabling more accurate forecasting of task feasibility and timelines. Emerging trends highlight integration of real-time data monitoring systems and blockchain for immutable progress tracking, ensuring greater transparency and accountability in project management. Enhanced machine learning algorithms are being designed to dynamically reassess task completion probabilities as new information arises, optimizing resource allocation and decision-making processes.
Complete Infographic
 libterm.com
libterm.com