Boolean complement refers to the operation of flipping a Boolean value to its opposite state, turning true into false and false into true. This fundamental concept is widely used in digital logic design, computer programming, and set theory to simplify expressions and enable efficient problem-solving. Explore the article to understand how Boolean complements impact logic circuits and programming conditions in greater detail.
Table of Comparison
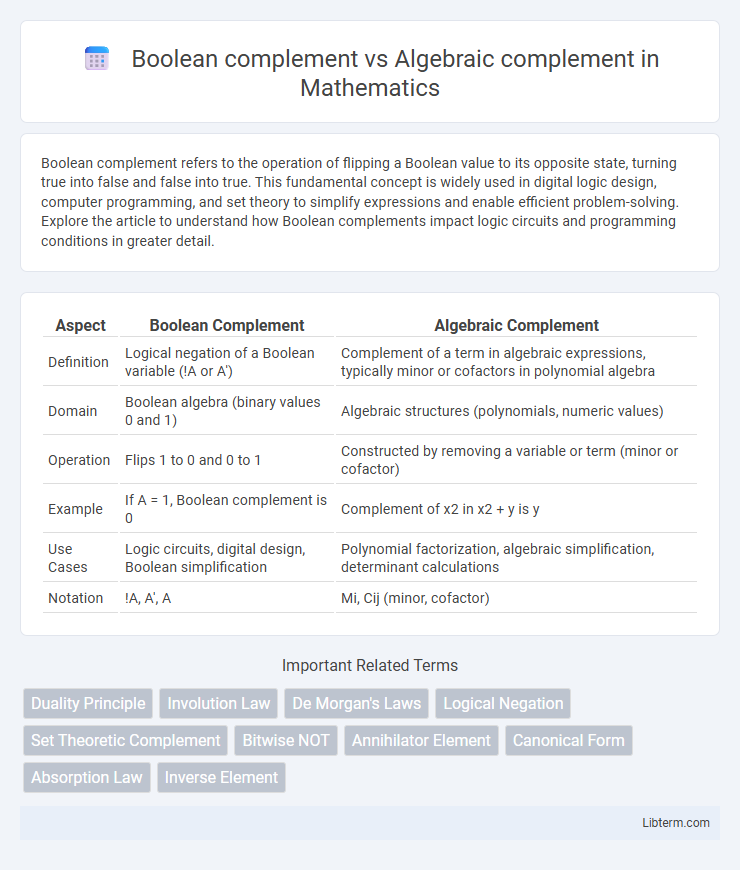
| Aspect | Boolean Complement | Algebraic Complement |
|---|---|---|
| Definition | Logical negation of a Boolean variable (!A or A') | Complement of a term in algebraic expressions, typically minor or cofactors in polynomial algebra |
| Domain | Boolean algebra (binary values 0 and 1) | Algebraic structures (polynomials, numeric values) |
| Operation | Flips 1 to 0 and 0 to 1 | Constructed by removing a variable or term (minor or cofactor) |
| Example | If A = 1, Boolean complement is 0 | Complement of x2 in x2 + y is y |
| Use Cases | Logic circuits, digital design, Boolean simplification | Polynomial factorization, algebraic simplification, determinant calculations |
| Notation | !A, A', A | Mi, Cij (minor, cofactor) |
Introduction to Complements in Mathematics
Boolean complement refers to the operation that inverts the value of a Boolean variable, switching true to false and false to true, essential in digital logic design. Algebraic complement, in contrast, involves subtracting a number from a fixed value like 1, often used in real or complex number systems to find additive inverses. Understanding these complements is crucial for mathematical logic, set theory, and algebraic structures, highlighting their distinct applications and properties.
Defining Boolean Complement
Boolean complement is a fundamental operation in Boolean algebra that inverts the value of a Boolean variable, transforming true (1) to false (0) and vice versa. It is denoted by a bar over the variable or a prime symbol, such as A or A', and follows specific laws including involution (double complement returns the original value). Unlike algebraic complement, which involves numerical negation in algebra, Boolean complement strictly deals with logical inversion within binary-valued systems.
Understanding Algebraic Complement
Algebraic complement refers to the value that, when added to a given number, results in a specific base number, commonly used in modular arithmetic and digital logic design, such as the 9's and 10's complement in decimal systems. Unlike the Boolean complement, which inverts binary values (0 to 1 and 1 to 0), the algebraic complement involves arithmetic subtraction from a defined modulus or base, providing a way to simplify subtraction operations. Understanding algebraic complement is essential for applications in computer arithmetic, error detection, and digital circuit optimization.
Key Differences Between Boolean and Algebraic Complements
Boolean complement involves inverting a logical variable's value, turning 1 into 0 and vice versa, essential in digital logic design and binary systems. Algebraic complement, often related to additive inverses in algebra, changes a number to its negative counterpart, such as transforming x to -x, crucial in solving equations and algebraic manipulations. The key difference is that Boolean complements operate within binary logic values (0 and 1), while algebraic complements deal with numbers and their additive inverses in a continuous numerical domain.
Fundamental Properties of Boolean Complements
Boolean complements satisfy the fundamental properties of involution (double complement returns the original variable) and the complementarity laws where the variable OR its complement equals 1 and the variable AND its complement equals 0. Algebraic complements, often in ring theory, rely on different axioms and may not follow the same involution property strictly. Boolean complement operations adhere to De Morgan's laws, ensuring consistency within Boolean algebra structures crucial for digital logic design and set theory applications.
Essential Properties of Algebraic Complements
Algebraic complements possess essential properties such as involution, where applying the complement operation twice returns the original element, and De Morgan's laws, which relate the complement of unions to intersections and vice versa. Unlike Boolean complements, algebraic complements operate within broader algebraic structures like lattices or rings, retaining properties like absorption and distributivity vital for simplifying expressions. These properties enable robust manipulation of elements while preserving structural integrity, making algebraic complements fundamental in areas such as lattice theory and ring theory.
Applications in Digital Logic and Algebra
Boolean complement in digital logic refers to the inversion of a binary variable, turning 1s into 0s and vice versa, essential for implementing logic gates like NOT, NAND, and NOR. Algebraic complement in algebra involves finding an element that, when combined with the original using addition or multiplication, yields an identity element, critical for solving equations and constructing algebraic structures. These complements enable efficient design and simplification of circuits in digital logic, while algebraic complements support abstract problem-solving in mathematical systems.
Truth Tables vs. Algebraic Examples
Boolean complement is defined by truth tables where the output is the inverse value of the input binary variable, showing 0 becomes 1 and 1 becomes 0, exemplified in digital logic circuits. Algebraic complement involves polynomial expressions over a field, illustrating complementarity through algebraic identities like (a + a') = 1 or (a * a') = 0 in Boolean algebra. Truth tables explicitly demonstrate the binary inversion for each input, while algebraic examples use symbolic manipulation to prove complement properties in equations.
Common Misconceptions Explained
Boolean complement refers to the logical negation operation in Boolean algebra where a variable switches between 1 and 0, representing true and false states. Algebraic complement involves finding the reciprocal or additive inverse in traditional algebra, often confused with Boolean complement due to similar terminology but fundamentally different contexts and operations. Common misconceptions arise when students apply algebraic complement rules to Boolean functions, leading to incorrect interpretations of logical negation and set operations.
Summary: Choosing the Right Complement Approach
Boolean complement simplifies expressions by inverting truth values in binary logic, making it ideal for digital circuit design and binary decision processes. Algebraic complement, involving additive inverses within algebraic structures like rings or fields, is essential in solving equations and simplifying polynomial expressions. Selecting the appropriate complement depends on context: use Boolean complement for logical operations and Boolean algebra, and algebraic complement for numerical computations and algebraic manipulations.
Boolean complement Infographic
 libterm.com
libterm.com