The Kronecker delta is a fundamental function in mathematics and physics, defined as d_ij = 1 if i = j and 0 otherwise, often used to represent identity matrices and simplify summations in tensor analysis. This discrete function plays a crucial role in linear algebra, signal processing, and quantum mechanics by acting as an identity element in index notation. Explore the rest of the article to understand how the Kronecker delta applies in various scientific contexts and mathematical operations.
Table of Comparison
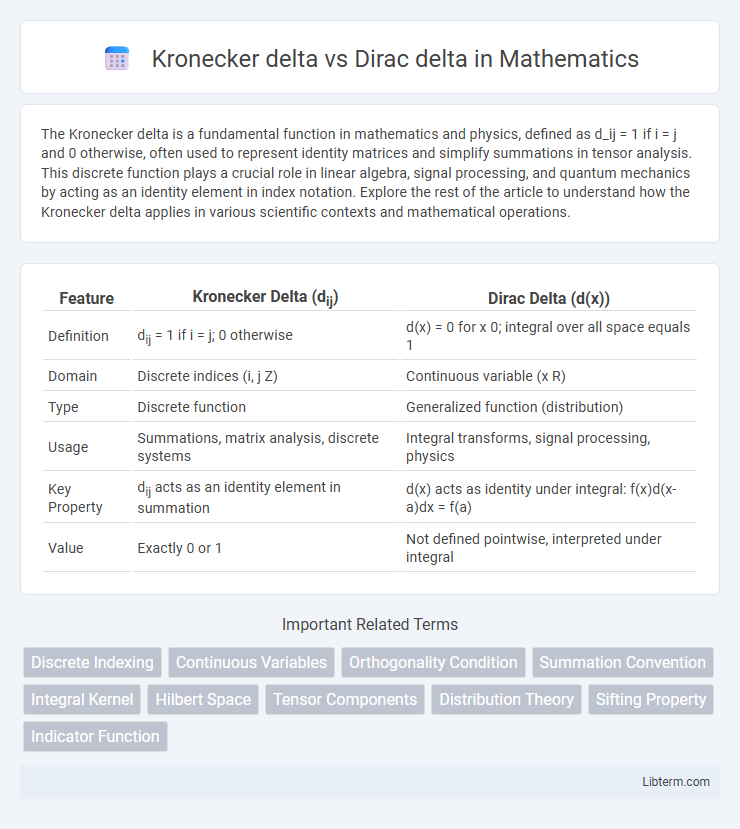
| Feature | Kronecker Delta (dij) | Dirac Delta (d(x)) |
|---|---|---|
| Definition | dij = 1 if i = j; 0 otherwise | d(x) = 0 for x 0; integral over all space equals 1 |
| Domain | Discrete indices (i, j Z) | Continuous variable (x R) |
| Type | Discrete function | Generalized function (distribution) |
| Usage | Summations, matrix analysis, discrete systems | Integral transforms, signal processing, physics |
| Key Property | dij acts as an identity element in summation | d(x) acts as identity under integral: f(x)d(x-a)dx = f(a) |
| Value | Exactly 0 or 1 | Not defined pointwise, interpreted under integral |
Introduction to Kronecker Delta and Dirac Delta
The Kronecker delta, denoted as d_ij, is a discrete function equal to 1 when indices i and j are identical and 0 otherwise, commonly used in summation expressions and matrix operations. The Dirac delta, d(x), is a continuous distribution defined as zero everywhere except at x = 0, where it is infinitely high such that its integral over the entire real line equals 1, playing a crucial role in integral transforms and signal processing. Both deltas serve as identity elements in their respective domains, with Kronecker delta operating in discrete index spaces and Dirac delta functioning in continuous variable contexts.
Mathematical Definitions
The Kronecker delta, denoted as \(\delta_{ij}\), is defined as a discrete function equal to 1 when indices \(i = j\) and 0 otherwise, commonly used in summation notation and finite-dimensional vector spaces. The Dirac delta function, represented as \(\delta(x)\), is a continuous distribution with the property \(\int_{-\infty}^{\infty} \delta(x) f(x) dx = f(0)\), acting as an identity under integral for continuous functions. While the Kronecker delta serves as the identity element in discrete sums, the Dirac delta functions as a generalized function or distribution in continuous integral transforms and signal processing.
Notation and Symbolic Representation
The Kronecker delta is denoted as \(\delta_{ij}\) and defined as a discrete function equal to 1 when indices \(i = j\) and 0 otherwise, commonly used in summation over discrete variables. The Dirac delta is represented by \(\delta(x)\) and functions as a continuous distribution with the property \(\int_{-\infty}^\infty \delta(x) f(x) \, dx = f(0)\), acting as an identity operator in integrals. While the Kronecker delta operates in discrete index spaces, the Dirac delta serves as a generalized function in continuous variable spaces, reflected in their distinct notations and domains.
Domains of Application
The Kronecker delta is predominantly used in discrete mathematics, linear algebra, and digital signal processing where indices are integers, serving as an identity element in summations over finite sets. The Dirac delta function is essential in continuous domains such as physics, engineering, and signal analysis, representing an idealized point impulse in continuous time or space. In quantum mechanics and distribution theory, the Dirac delta facilitates integral transforms and eigenfunction expansions, contrasting the Kronecker delta's role in matrix and tensor operations.
Discrete vs. Continuous Nature
The Kronecker delta is a discrete function defined as d_ij, equaling 1 when i = j and 0 otherwise, primarily used in summations over discrete indices in linear algebra and signal processing. In contrast, the Dirac delta is a continuous distribution d(x), characterized by an infinite spike at x = 0 with integral equal to 1, utilized in continuous systems like physics and engineering to model point impulses. These distinct definitions highlight the Kronecker delta's role in discrete settings and the Dirac delta's application in continuous domains.
Key Properties and Formulas
The Kronecker delta, defined as \( \delta_{ij} = 1 \) if \( i = j \) and 0 otherwise, serves as an identity element in discrete summations and matrix operations. The Dirac delta \( \delta(x) \), a distribution rather than a function, satisfies \( \int_{-\infty}^{\infty} \delta(x) \, dx = 1 \) and acts as an identity under integration by extracting function values at specific points, i.e., \( \int_{-\infty}^\infty f(x) \delta(x - a) \, dx = f(a) \). Unlike the discrete Kronecker delta, the Dirac delta is continuous and instrumental in signal processing and solving differential equations with boundary conditions.
Common Uses in Physics and Engineering
The Kronecker delta is widely used in discrete systems and linear algebra, particularly for indexing and simplifying sums in quantum mechanics and signal processing. The Dirac delta, a continuous distribution, serves as an idealized point source or impulse in classical and quantum physics, crucial for modeling impulse responses and Green's functions. Both deltas facilitate the representation of orthogonality and identity properties within their respective discrete and continuous domains.
Comparisons in Linear Algebra and Calculus
The Kronecker delta d_ij functions as an identity element in linear algebra, acting as a discrete selector that equals 1 when indices i and j are identical and 0 otherwise, facilitating matrix operations and basis transformations. In contrast, the Dirac delta d(x) serves as a distribution in calculus, representing an idealized point mass that is zero everywhere except at x = 0, where it integrates to one, often used to model impulse responses and simplify integral expressions. While the Kronecker delta operates over discrete index sets in finite-dimensional vector spaces, the Dirac delta extends to continuous domains in infinite-dimensional function spaces, underscoring their complementary roles across mathematical disciplines.
Examples and Illustrative Problems
The Kronecker delta, defined as d_ij = 1 if i = j and 0 otherwise, is commonly used in discrete settings such as matrix operations and summations, for example, in simplifying expressions like _j A_j d_ij = A_i. The Dirac delta, d(x), acts as a continuous distribution with properties like f(x)d(x - a) dx = f(a), serving as an idealized point mass or impulse in physics and engineering problems, such as modeling point charges or impulses in differential equations. Illustrative problems include using the Kronecker delta in tensor contractions and employing the Dirac delta for Green's function solutions in boundary value problems.
Summary of Differences and Similarities
The Kronecker delta, d_ij, is defined for discrete indices and equals 1 when i=j and 0 otherwise, serving as the identity element in summations over discrete variables. The Dirac delta, d(x), is a distribution over continuous variables with the property that it is zero everywhere except at x=0, where it is infinitely peaked, and its integral over the entire real line equals one. Both functions act as identity elements in their respective domains: the Kronecker delta in discrete summation and the Dirac delta in continuous integration, facilitating selection or filtering of specific components or values.
Kronecker delta Infographic
 libterm.com
libterm.com