Partial order defines a binary relation on a set where elements are compared in a way that is reflexive, antisymmetric, and transitive, allowing some elements to remain incomparable. This concept is fundamental in fields like mathematics and computer science for structuring data where hierarchy is not strictly linear. Explore the rest of the article to understand how partial orders apply in various real-world scenarios and theoretical frameworks.
Table of Comparison
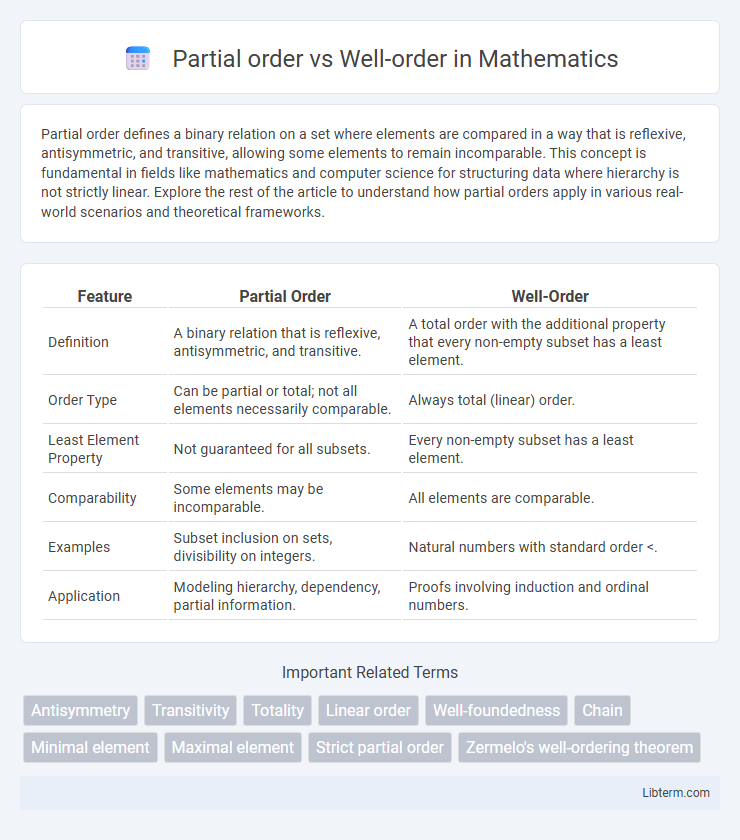
| Feature | Partial Order | Well-Order |
|---|---|---|
| Definition | A binary relation that is reflexive, antisymmetric, and transitive. | A total order with the additional property that every non-empty subset has a least element. |
| Order Type | Can be partial or total; not all elements necessarily comparable. | Always total (linear) order. |
| Least Element Property | Not guaranteed for all subsets. | Every non-empty subset has a least element. |
| Comparability | Some elements may be incomparable. | All elements are comparable. |
| Examples | Subset inclusion on sets, divisibility on integers. | Natural numbers with standard order <. |
| Application | Modeling hierarchy, dependency, partial information. | Proofs involving induction and ordinal numbers. |
Introduction to Partial Orders and Well-Orders
A partial order is a binary relation over a set that is reflexive, antisymmetric, and transitive, allowing elements to be compared in a non-linear fashion. A well-order is a special type of partial order where every non-empty subset has a least element, ensuring a total or linear order with a minimal element property. These concepts form the foundation for analyzing hierarchical structures and order types in mathematics and computer science.
Defining Partial Orders: Key Concepts
Partial orders are binary relations defined on a set that are reflexive, antisymmetric, and transitive, meaning every element relates to itself, no two distinct elements precede each other simultaneously, and the relation is consistent over chains. Key concepts include comparability, where not all pairs of elements must be comparable, distinguishing partial orders from total orders. Partial orders enable the structuring of elements with inherent hierarchy or precedence without requiring a linear sequence.
The Structure of Well-Ordered Sets
Well-ordered sets are partially ordered sets with the added property that every non-empty subset has a least element, ensuring a unique minimal element exists in all subsets. The structure of well-ordered sets enables transfinite induction and recursion, as their order type can be described by ordinals, providing a comprehensive framework for indexing sequences beyond natural numbers. Unlike general partial orders, well-orders are linear and well-founded, which guarantees no infinite descending chains and a strict hierarchical organization.
Fundamental Differences Between Partial and Well-Orders
Partial orders allow elements to be incomparable, forming a reflexive, antisymmetric, and transitive relation without requiring every pair to be related, whereas well-orders are total orders that are well-founded, meaning every non-empty subset has a least element. The fundamental difference lies in the comparability and minimal element requirements: well-orders ensure a complete linear ordering and guarantee minimal elements exist in every subset, while partial orders lack these constraints. This distinction impacts their applications in set theory, order theory, and proofs involving induction and recursion principles.
Examples of Partial Orders in Mathematics
Partial orders appear in set theory with the subset relation among sets, where some sets are comparable based on inclusion but not all. In algebra, divisibility relations on integers form a partial order since some numbers divide others without a total ordering. Another example comes from graph theory, where reachability in directed acyclic graphs defines a partial order among vertices, capturing a hierarchy without cycles.
Well-Order Examples and Properties
Well-order is a strict total order where every non-empty subset has a least element, exemplified by the natural numbers under the usual <= relation. This structure ensures no infinite descending sequences exist, which is crucial for proofs by transfinite induction. Well-ordered sets exhibit properties such as comparability of every pair of elements, the existence of minimal elements in subsets, and support for ordinal arithmetic.
Comparability: Partial Orders vs. Total Orders
Partial orders allow elements to be incomparable, meaning not all pairs of elements need to be related by the order relation. Total orders, also known as linear orders, require comparability, where every pair of elements is comparable under the order relation. Well-orders are a special type of total order with the additional property that every non-empty subset has a least element, ensuring both comparability and well-foundedness.
Importance of Well-Ordering Principle
The Well-Ordering Principle asserts that every non-empty set of natural numbers has a least element, which is fundamental for proofs involving induction and recursion. Unlike partial orders, which allow incomparable elements, well-orders ensure a total, linear ordering that enables the systematic construction and analysis of sequences. This principle underpins key areas in set theory, number theory, and mathematical logic by guaranteeing minimal elements essential for defining functions and proving properties across well-ordered sets.
Applications of Partial and Well-Orders
Partial orders are essential in computer science for modeling hierarchical data structures, such as file systems and task scheduling, where elements have a defined order without requiring comparability between all pairs. Well-orders play a crucial role in set theory and logic, enabling transfinite induction and ordinal analysis, which are fundamental in proving properties of infinite sequences and hierarchies. In mathematics, partial orders facilitate lattice theory and domain theory applications, while well-orders provide a basis for ordinal numbers and guarantee the existence of minimal elements in every non-empty subset.
Summary and Key Takeaways
A partial order is a binary relation that is reflexive, antisymmetric, and transitive, allowing elements to be compared in a non-linear hierarchy where some pairs remain incomparable. A well-order is a special type of total order with the additional property that every non-empty subset has a least element, ensuring no infinite descending sequences exist. Understanding the distinction clarifies structural differences essential in set theory, order theory, and their applications in mathematical logic and computer science.
Partial order Infographic
 libterm.com
libterm.com