Tannakian categories provide a powerful framework connecting category theory with group schemes, enabling the study of algebraic structures through tensor categories equipped with fiber functors. These categories play a crucial role in modern algebraic geometry and representation theory by translating complex geometric problems into categorical language. Explore the rest of the article to deepen your understanding of how Tannakian categories bridge abstract mathematics and concrete algebraic applications.
Table of Comparison
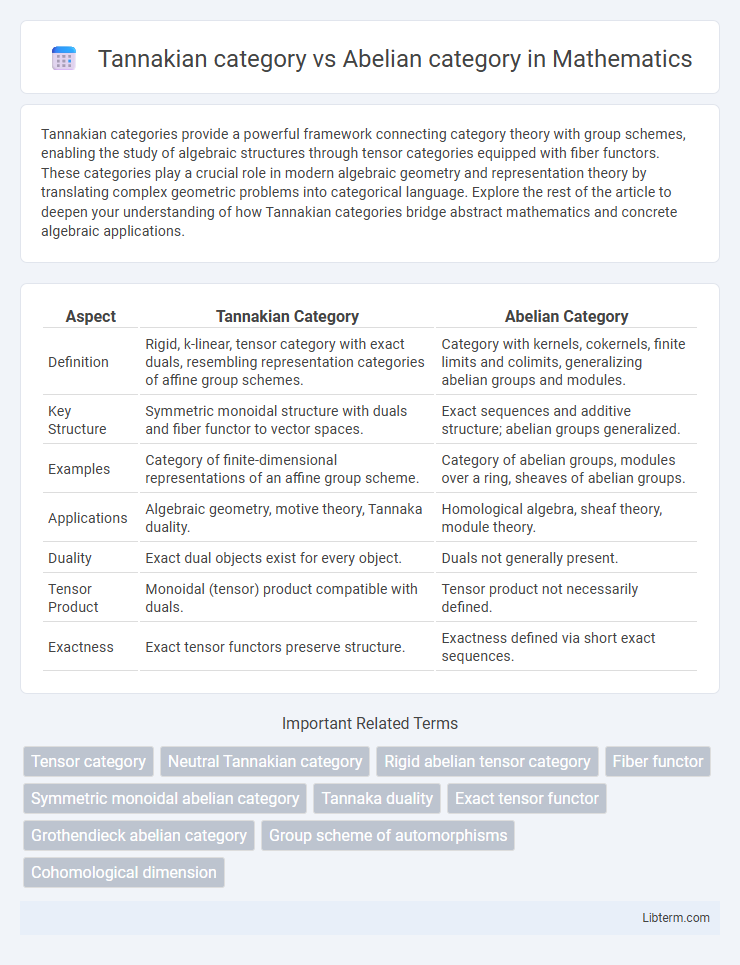
| Aspect | Tannakian Category | Abelian Category |
|---|---|---|
| Definition | Rigid, k-linear, tensor category with exact duals, resembling representation categories of affine group schemes. | Category with kernels, cokernels, finite limits and colimits, generalizing abelian groups and modules. |
| Key Structure | Symmetric monoidal structure with duals and fiber functor to vector spaces. | Exact sequences and additive structure; abelian groups generalized. |
| Examples | Category of finite-dimensional representations of an affine group scheme. | Category of abelian groups, modules over a ring, sheaves of abelian groups. |
| Applications | Algebraic geometry, motive theory, Tannaka duality. | Homological algebra, sheaf theory, module theory. |
| Duality | Exact dual objects exist for every object. | Duals not generally present. |
| Tensor Product | Monoidal (tensor) product compatible with duals. | Tensor product not necessarily defined. |
| Exactness | Exact tensor functors preserve structure. | Exactness defined via short exact sequences. |
Introduction to Tannakian and Abelian Categories
Tannakian categories provide a framework to study group schemes through tensor categories equipped with a fiber functor, establishing an equivalence with representations of an affine group scheme. Abelian categories serve as an abstract setting for homological algebra, generalizing categories of modules by allowing kernels, cokernels, and exact sequences. Understanding Tannakian categories relies on the underlying abelian category structure enriched with tensor products, symmetry, and duals, connecting algebraic geometry and category theory.
Historical Background and Motivation
Tannakian categories originated in the 1950s through the work of Andre Weil and later formalized by Saavedra Rivano in the 1960s to provide an abstract framework for studying representations of algebraic groups via tensor categories. Abelian categories, introduced by Alexander Grothendieck in the 1950s, were motivated by the need to generalize module theory and homological algebra in a categorical setting. The development of Tannakian categories was driven by the desire to reconstruct group schemes from their category of representations, a problem not addressed by the broader and more foundational concept of Abelian categories.
Defining Abelian Categories
Abelian categories are additive categories with kernels and cokernels where every monomorphism and epimorphism is normal, ensuring exact sequences can be defined and homological algebra can be developed. Tannakian categories, by contrast, are rigid abelian tensor categories equipped with a fiber functor to vector spaces, allowing a reconstruction of affine group schemes via Tannaka duality. The defining property of abelian categories centers on the existence and exactness of kernels and cokernels, forming an environment suitable for the study of exact sequences and homological constructs.
Essential Properties of Tannakian Categories
Tannakian categories are rigid, abelian tensor categories equipped with a fiber functor to the category of vector spaces, allowing reconstruction of affine group schemes via Tannaka duality. Essential properties include the presence of a neutral fiber functor, exactness, and the existence of duals for every object, which distinguishes them from general abelian categories. These characteristics enable a deep connection between algebraic groups and category theory, facilitating the study of algebraic structures through representations.
Key Similarities Between Tannakian and Abelian Categories
Tannakian categories and Abelian categories both possess a rich structure that supports exact sequences and kernels, enabling the study of morphisms and objects in a robust algebraic framework. Both categories are additive, allowing direct sums and the existence of zero objects, which facilitate the decomposition of complex structures into simpler components. The presence of a tensor product in Tannakian categories extends the Abelian category structure by introducing additional constraints, yet both maintain fundamental homological properties critical for their applications in representation theory and algebraic geometry.
Distinctive Features of Tannakian Categories
Tannakian categories are rigid, neutral tannakian categories equipped with a fiber functor to the category of vector spaces over a field, enabling a deep connection to affine group schemes through Tannaka duality. Unlike general abelian categories, Tannakian categories are tensor categories that are abelian, k-linear, and possess a fiber functor that reflects their symmetry and realization as representations of a pro-algebraic group. The rigidity and existence of a fiber functor make Tannakian categories particularly powerful in connecting categorical structures to group-theoretic and representation-theoretic contexts.
Role of Tensor Structures in Tannakian Categories
Tannakian categories are rigid abelian tensor categories equipped with a fiber functor to vector spaces, where the tensor structure plays a crucial role in reconstructing affine group schemes via Tannaka duality. The tensor product allows for the encoding of additional symmetry and monoidal information that is absent in general abelian categories, enabling the characterization of representations of algebraic groups through categorical data. This tensorial framework distinguishes Tannakian categories by linking their objects and morphisms directly to the representation theory of affine group schemes.
Functorial Relationships and Fiber Functors
Tannakian categories are rigid abelian tensor categories equipped with fiber functors that are exact, faithful, and tensor-preserving, enabling reconstruction of affine group schemes via Tannaka duality. Abelian categories emphasize exact sequences and kernel-cokernel structures without inherent tensor product requirements, lacking canonical fiber functors unless additional structure is specified. Functorial relationships in Tannakian categories revolve around fiber functors mapping to vector spaces, which encode representation-theoretic data, while in general abelian categories, functors primarily preserve exactness and additive structure without necessarily reflecting group symmetries.
Applications in Algebraic Geometry and Representation Theory
Tannakian categories provide a powerful framework in algebraic geometry for reconstructing group schemes from tensor categories, facilitating deep insights into the symmetry structures of algebraic varieties. Abelian categories offer a broad and flexible environment for homological algebra, enabling the development of cohomology theories fundamental to modern algebraic geometry. In representation theory, Tannakian categories bridge group representations and category theory, while abelian categories underpin the study of modules and morphisms, supporting classification and decomposition results.
Summary and Future Directions
Tannakian categories generalize Abelian categories by incorporating a fiber functor to vector spaces, enabling reconstruction of affine group schemes through Tannaka duality. While Abelian categories provide a robust framework for homological algebra, Tannakian categories extend these concepts to encompass representation theory and algebraic geometry with deeper structural insights. Future research aims to explore non-neutral Tannakian categories, enhance connections with motivic Galois groups, and apply these structures to quantum groups and categorical symmetry.
Tannakian category Infographic
 libterm.com
libterm.com