The cup product is a fundamental operation in algebraic topology that combines cohomology classes to form higher-dimensional classes, enriching the structure of cohomology rings. This bilinear operation provides insights into the interplay between topological spaces and algebraic invariants, helping to classify and distinguish complex shapes. Explore the rest of this article to understand how the cup product reveals deeper geometric and topological properties.
Table of Comparison
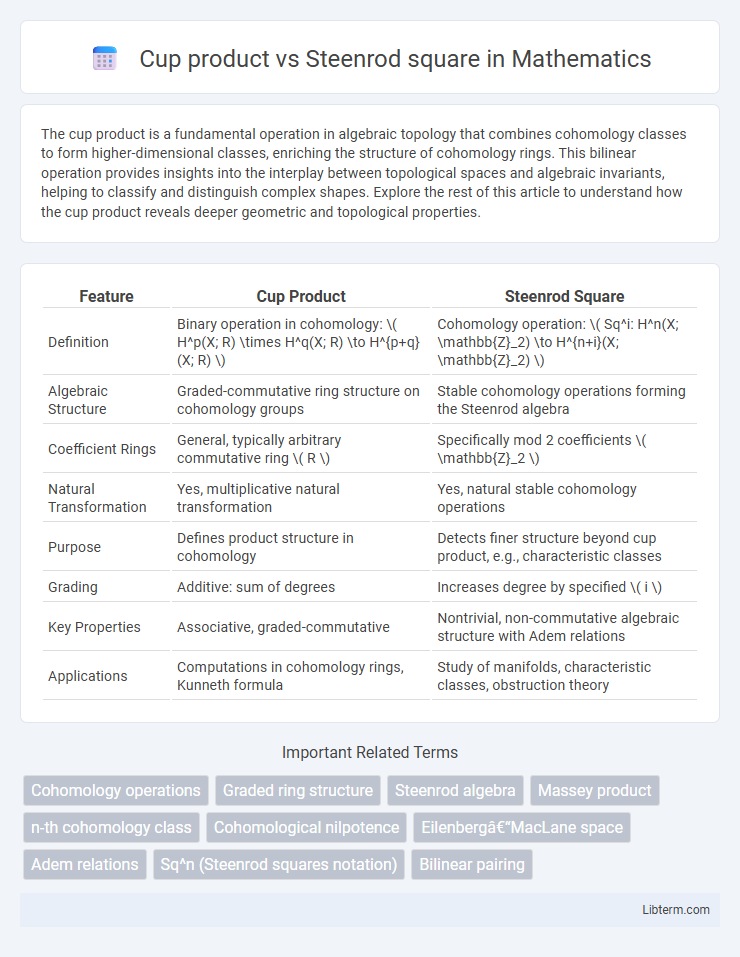
| Feature | Cup Product | Steenrod Square |
|---|---|---|
| Definition | Binary operation in cohomology: \( H^p(X; R) \times H^q(X; R) \to H^{p+q}(X; R) \) | Cohomology operation: \( Sq^i: H^n(X; \mathbb{Z}_2) \to H^{n+i}(X; \mathbb{Z}_2) \) |
| Algebraic Structure | Graded-commutative ring structure on cohomology groups | Stable cohomology operations forming the Steenrod algebra |
| Coefficient Rings | General, typically arbitrary commutative ring \( R \) | Specifically mod 2 coefficients \( \mathbb{Z}_2 \) |
| Natural Transformation | Yes, multiplicative natural transformation | Yes, natural stable cohomology operations |
| Purpose | Defines product structure in cohomology | Detects finer structure beyond cup product, e.g., characteristic classes |
| Grading | Additive: sum of degrees | Increases degree by specified \( i \) |
| Key Properties | Associative, graded-commutative | Nontrivial, non-commutative algebraic structure with Adem relations |
| Applications | Computations in cohomology rings, Kunneth formula | Study of manifolds, characteristic classes, obstruction theory |
Introduction to Cup Product and Steenrod Square
The Cup product is a bilinear operation in cohomology that combines two cohomology classes, producing a new class in the sum of their degrees, fundamental for defining ring structures in cohomology theories. Steenrod squares are cohomology operations defined on mod 2 cohomology, providing stable homotopy invariants and enriching the structure with secondary cohomology operations beyond the Cup product. These operations interact in complex ways, as Steenrod squares generalize and extend the information captured by the basic cup product in algebraic topology.
Historical Background and Development
The cup product, introduced by Eilenberg and Steenrod in the early 1940s, forms the foundation of cohomology ring structures by combining cohomology classes in algebraic topology. Steenrod squares, developed by Norman Steenrod in the late 1940s, extended the cohomology operations by defining stable cohomology operations that act on mod 2 cohomology. These advancements revolutionized algebraic topology by providing tools for distinguishing and classifying topological spaces beyond classical invariants.
Mathematical Foundations of Cup Product
The cup product is a fundamental operation in cohomology theory that combines cohomology classes to form a graded-commutative ring structure on the cohomology groups of a topological space. It is defined using the chain-level product induced from the diagonal map on the space, capturing algebraic information about intersections and compositions of cycles. In contrast, the Steenrod square operates as a cohomology operation in mod 2 cohomology that refines the cup product structure by encoding additional homotopy-theoretic invariants beyond those detected by the standard cup product.
Understanding Steenrod Squares in Cohomology
Steenrod squares are cohomology operations defined on mod 2 cohomology that extend the classical cup product by incorporating secondary structure, providing richer algebraic invariants in topology. Unlike the bilinear cup product, Steenrod squares satisfy axioms like the Cartan formula and Adem relations, enabling computations in stable cohomotopy and characteristic classes of manifolds. Understanding Steenrod squares involves analyzing their action on cohomology rings, especially mod 2, revealing deeper symmetries and obstructions beyond what cup products capture.
Algebraic Properties and Differences
The cup product in cohomology is a graded-commutative bilinear operation that combines cohomology classes to form higher-degree classes, fulfilling the associative law and distributing over addition. Steenrod squares are stable cohomology operations defined on mod 2 cohomology groups, enhancing structure by producing new classes in double the degree minus a shift, and they satisfy Adem relations governing their compositions. Unlike the cup product, which is inherently multiplicative and product-like, Steenrod squares encode secondary cohomological information and are nontrivial cohomology operations that do not arise from simple bilinear constructions.
Computational Techniques for Each Operation
Computational techniques for the cup product in cohomology typically involve explicit chain-level representatives and the Alexander-Whitney map to define the product on cochains, facilitating straightforward algorithmic implementations in simplicial complexes. Steenrod squares require more intricate methods, employing the properties of the cohomology operations and the Adem relations, often utilizing combinatorial formulas or computer algebra systems designed for secondary cohomology operations to handle their non-linear and unstable nature. Efficient computation of Steenrod squares leverages spectral sequences and minimal resolutions, contrasting with the generally simpler tensor product-based computations used for cup products.
Geometric and Topological Interpretations
The cup product in cohomology provides a bilinear operation combining classes to reflect the intersection structure of submanifolds, capturing geometric information about how spaces intersect topologically. Steenrod squares are stable cohomology operations that enrich the cup product by encoding finer mod 2 phenomena, revealing subtle topological properties such as the nontrivial twisting of bundles and characteristic classes. Geometrically, Steenrod squares can be interpreted via intersection theory with singularities and framed manifolds, distinguishing spaces that share the same cup product but differ in their stable homotopy features.
Applications in Algebraic Topology
Cup products enable the construction of cohomology rings that classify topological spaces by encoding intersection properties of subspaces. Steenrod squares, as cohomology operations, provide finer invariants distinguishing spaces that share identical cohomology rings by detecting higher-order structure and torsion phenomena. Applications in algebraic topology include the classification of manifolds, obstruction theory, and the computation of characteristic classes through the interplay of cup products and Steenrod squares.
Comparing Cup Product and Steenrod Square
Cup products in cohomology provide a graded-commutative multiplication structure between cohomology classes, combining elements to form higher-degree classes and encoding the algebraic structure of topological spaces. Steenrod squares, on the other hand, are stable cohomology operations defined in mod 2 cohomology that detect additional structure beyond cup products by acting as natural transformations increasing degree and commuting with cohomology homomorphisms. Comparing both, cup products reflect the algebraic graded ring structure, while Steenrod squares capture subtle nonlinear phenomena and secondary operations critical for distinguishing spaces with identical cup product structures.
Summary and Future Directions
The Cup product serves as a fundamental bilinear operation in cohomology, enabling the construction of ring structures that capture topological invariants, while Steenrod squares extend these operations to mod 2 cohomology with additional nontrivial properties encoding finer homotopical information. Current research explores generalized cohomology theories and equivariant settings to unify and enhance the computational power of these operations. Future directions aim to develop higher-order cohomological operations and apply them to areas such as stable homotopy theory and topological data analysis for deeper structural insights.
Cup product Infographic
 libterm.com
libterm.com