Dirichlet series are infinite series of the form \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), where \(a_n\) are complex coefficients and \(s\) is a complex variable. These series play a crucial role in analytic number theory, especially in the study of prime number distribution through functions like the Riemann zeta function. Explore the rest of the article to understand the properties and applications of Dirichlet series in greater depth.
Table of Comparison
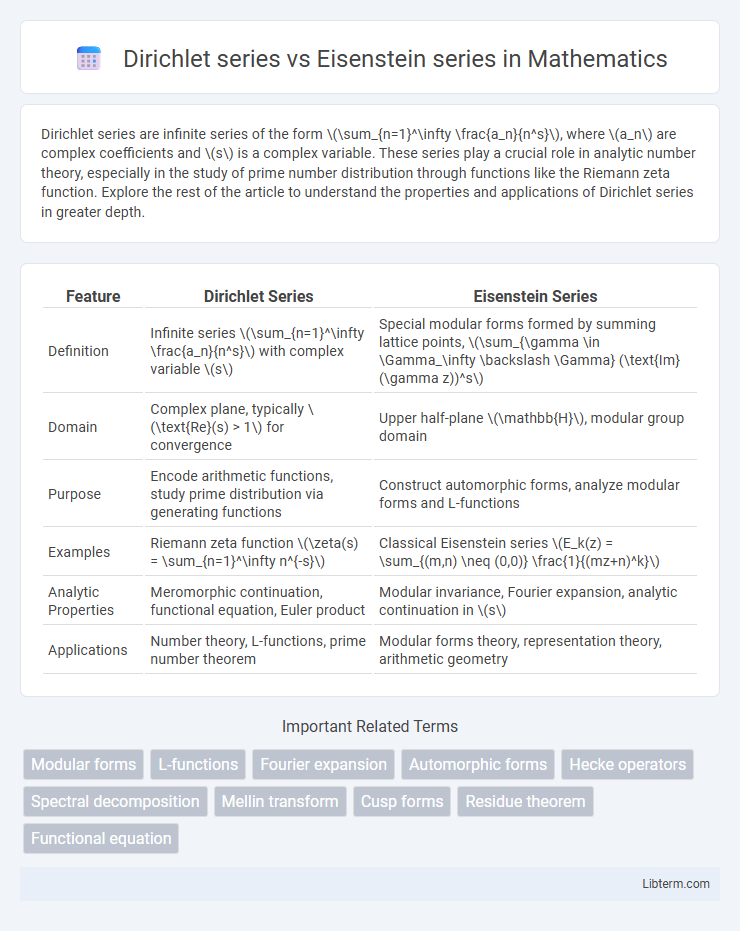
| Feature | Dirichlet Series | Eisenstein Series |
|---|---|---|
| Definition | Infinite series \(\sum_{n=1}^\infty \frac{a_n}{n^s}\) with complex variable \(s\) | Special modular forms formed by summing lattice points, \(\sum_{\gamma \in \Gamma_\infty \backslash \Gamma} (\text{Im}(\gamma z))^s\) |
| Domain | Complex plane, typically \(\text{Re}(s) > 1\) for convergence | Upper half-plane \(\mathbb{H}\), modular group domain |
| Purpose | Encode arithmetic functions, study prime distribution via generating functions | Construct automorphic forms, analyze modular forms and L-functions |
| Examples | Riemann zeta function \(\zeta(s) = \sum_{n=1}^\infty n^{-s}\) | Classical Eisenstein series \(E_k(z) = \sum_{(m,n) \neq (0,0)} \frac{1}{(mz+n)^k}\) |
| Analytic Properties | Meromorphic continuation, functional equation, Euler product | Modular invariance, Fourier expansion, analytic continuation in \(s\) |
| Applications | Number theory, L-functions, prime number theorem | Modular forms theory, representation theory, arithmetic geometry |
Introduction to Dirichlet Series and Eisenstein Series
Dirichlet series are infinite series of the form a_n / n^s, fundamental in analytic number theory for encoding arithmetic information and studying L-functions. Eisenstein series are special types of modular forms constructed as infinite sums over lattice points, playing a crucial role in the theory of modular forms and automorphic functions. Both series serve as essential tools in understanding complex analytic properties and symmetries within number theory.
Historical Development and Mathematical Significance
Dirichlet series, originating from Johann Peter Gustav Lejeune Dirichlet's 19th-century work, play a fundamental role in analytic number theory by encoding arithmetic functions into complex analytic objects, crucial for understanding prime distribution through the Riemann zeta function. Eisenstein series, developed by Gotthold Eisenstein in the mid-19th century, are automorphic forms fundamental in the theory of modular forms, linking complex analysis, number theory, and representation theory. The interplay between Dirichlet and Eisenstein series underpins significant advances in the Langlands program and modern arithmetic geometry, reflecting their profound mathematical significance.
Formal Definitions and Fundamental Properties
A Dirichlet series is a function defined as \( \sum_{n=1}^\infty \frac{a_n}{n^s} \), where \( s \) is a complex variable and \( a_n \) are complex coefficients, commonly used in analytic number theory for encoding arithmetic data. An Eisenstein series is a type of modular form defined on the upper half-plane, typically as \( E_k(z) = \sum_{(m,n) \neq (0,0)} \frac{1}{(mz + n)^k} \), exhibiting automorphic properties under the action of the modular group \( SL_2(\mathbb{Z}) \). While Dirichlet series focus on complex series with multiplicative coefficients relevant to L-functions and prime distribution, Eisenstein series incorporate harmonic analysis and modular symmetry, serving as fundamental examples of modular forms with transformation behavior under modular group actions.
Analytic Structure and Domains of Convergence
Dirichlet series, typically expressed as \( \sum_{n=1}^\infty a_n n^{-s} \), possess a half-plane of absolute convergence determined by the real part of \( s \), often linked to the abscissa of convergence. In contrast, Eisenstein series, as automorphic forms on the upper half-plane, exhibit meromorphic continuation across the entire complex plane with poles related to spectral parameters and lattice symmetries. The analytic structure of Dirichlet series is dominated by singularities such as poles and sometimes branch cuts within half-planes, whereas Eisenstein series feature more intricate analytic continuation governed by functional equations and modular invariance.
Connections to Modular Forms and L-functions
Dirichlet series serve as generating functions for arithmetic functions and play a crucial role in defining L-functions, which encode deep number-theoretic properties and are closely linked to modular forms. Eisenstein series are specific modular forms constructed as infinite series with explicit Fourier expansions, directly related to L-functions through their constant terms, revealing connections to special values of Dirichlet L-series. The interplay between Eisenstein series and Dirichlet series in the theory of modular forms provides foundational tools for studying automorphic representations and analytic properties of L-functions.
Applications in Number Theory and Arithmetic
Dirichlet series, such as the Riemann zeta function, are fundamental tools in analytic number theory used to study the distribution of prime numbers through their Euler product representations and analytic continuation. Eisenstein series arise in the context of modular forms and automorphic forms, playing a crucial role in understanding arithmetic properties of lattices and modular curves, as well as generating explicit formulas for special values of L-functions. Both series connect deeply to the theory of L-functions and modularity, facilitating insights into class number formulas, modularity lifting, and the behavior of arithmetic functions.
Spectral Interpretation and Representation Theory
Dirichlet series are complex functions often expressed as infinite sums \( \sum_{n=1}^\infty a_n n^{-s} \) and play a key role in analytic number theory by encoding arithmetical information through their coefficients \( a_n \). Eisenstein series, constructed on symmetric spaces or modular groups, arise naturally in the spectral decomposition of automorphic forms and represent eigenfunctions of the Laplacian, providing explicit examples of automorphic representations. The spectral interpretation of Eisenstein series reveals their role in decomposing \( L^2 \)-spaces on arithmetic quotients, while Dirichlet series are linked to these spectral objects via \( L \)-functions associated with automorphic forms, establishing a deep connection through representation theory.
Comparison of Fourier Expansions
Dirichlet series typically have a Fourier expansion involving multiplicative arithmetic functions defined over integers, emphasizing the analytic properties of L-functions and their coefficients. Eisenstein series exhibit a more structured Fourier expansion characterized by sums over lattice points, incorporating modular forms and automorphic factors with explicit constant and non-constant terms. The comparison highlights that Dirichlet series expansions focus on number-theoretic sequences, while Eisenstein series expansions reflect deep connections to modular symmetry and harmonic analysis.
Key Differences in Functional Equations
Dirichlet series typically satisfy functional equations relating values at \(s\) and \(1-s\), often involving gamma factors and character twists, reflecting their role in number theory and L-functions. Eisenstein series possess more intricate functional equations under the action of the modular group, encoding automorphic transformations and exhibiting meromorphic continuation across the complex plane. The key difference lies in the modular symmetry and transformation properties of Eisenstein series versus the reflection-type functional equations characteristic of Dirichlet series.
Open Problems and Research Directions
Open problems in Dirichlet series involve understanding the distribution of their zeros and establishing universality properties across various families, which impacts analytic number theory and the study of L-functions. Research on Eisenstein series focuses on their spectral decomposition and the role in automorphic forms, with open questions about their Fourier coefficients and connections to Langlands program. Both series types drive progress in understanding deep arithmetic symmetries and modular forms, offering fertile ground for exploring new conjectures in analytic and algebraic number theory.
Dirichlet series Infographic
 libterm.com
libterm.com