Algebraic varieties are fundamental objects in algebraic geometry, characterized as the solution sets of systems of polynomial equations over a field. They exhibit rich geometric and topological structures that connect abstract algebra with geometry, enabling deep insights into equations and their symmetries. Explore the rest of the article to understand how algebraic varieties underpin modern mathematical theories and applications.
Table of Comparison
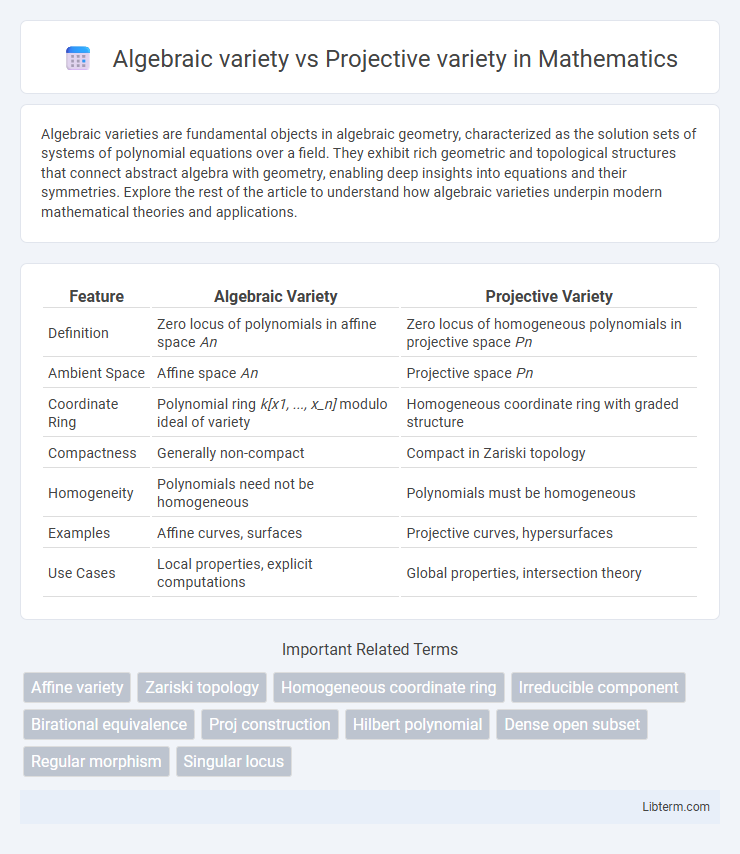
| Feature | Algebraic Variety | Projective Variety |
|---|---|---|
| Definition | Zero locus of polynomials in affine space An | Zero locus of homogeneous polynomials in projective space Pn |
| Ambient Space | Affine space An | Projective space Pn |
| Coordinate Ring | Polynomial ring k[x1, ..., x_n] modulo ideal of variety | Homogeneous coordinate ring with graded structure |
| Compactness | Generally non-compact | Compact in Zariski topology |
| Homogeneity | Polynomials need not be homogeneous | Polynomials must be homogeneous |
| Examples | Affine curves, surfaces | Projective curves, hypersurfaces |
| Use Cases | Local properties, explicit computations | Global properties, intersection theory |
Introduction to Algebraic Varieties
Algebraic varieties are the fundamental objects of study in algebraic geometry, defined as the solution sets of systems of polynomial equations over a field. Projective varieties are a special class of algebraic varieties that are defined in projective space, allowing the inclusion of points at infinity and providing a more compact and homogeneous geometric framework. The introduction to algebraic varieties involves understanding affine varieties as zero loci in affine space and projective varieties as zero loci in projective space, highlighting the role of homogeneous coordinates and the importance of these structures in capturing geometric properties algebraically.
Defining Projective Varieties
Projective varieties are algebraic varieties defined as the zero loci of homogeneous polynomials in projective space \(\mathbb{P}^n\), where points are equivalence classes of nonzero vectors under scalar multiplication. Unlike affine varieties, projective varieties include points at infinity, ensuring compactness and enabling the use of intersection theory. The defining ideal of a projective variety is a homogeneous ideal in the polynomial ring, reflecting the embedding into projective space and preserving geometric properties under projective transformations.
Key Differences Between Algebraic and Projective Varieties
Algebraic varieties are the solution sets of polynomial equations defined over affine space, characterized by coordinates in a finite-dimensional vector space, while projective varieties reside in projective space where points are defined up to scalar multiplication, incorporating points at infinity. Key differences include the treatment of infinity, with projective varieties compactifying affine varieties by adding points at infinity, and the homogeneous nature of defining polynomials in projective varieties versus arbitrary polynomials in algebraic varieties. Additionally, projective varieties facilitate the study of geometric properties invariant under projective transformations, whereas algebraic varieties focus on properties within Euclidean or affine settings.
Affine Varieties vs. Projective Varieties
Affine varieties are defined as the set of common zeros of polynomial functions within affine space, characterized by coordinates in \(\mathbb{A}^n\), where solutions are not considered up to scale. Projective varieties, in contrast, reside in projective space \(\mathbb{P}^n\), and account for equivalence classes of points under scalar multiplication, accommodating homogeneous coordinates and enabling compactification of affine varieties. The transition from affine to projective varieties involves homogenizing polynomials, which preserves geometric properties while ensuring completeness and allowing the study of varieties at infinity.
Coordinate Rings and Homogeneous Ideals
Algebraic varieties correspond to coordinate rings defined as quotients of polynomial rings by prime ideals, capturing affine geometric structure, whereas projective varieties associate with coordinate rings graded by degree, constructed via homogeneous ideals in a polynomial ring. The homogeneous ideal ensures that the projective variety respects scaling relations intrinsic to projective space, with its coordinate ring formed from equivalence classes of homogeneous polynomials. This distinction in the structure of ideals and coordinate rings reflects the transition from affine to projective geometry, crucial for analyzing properties invariant under projective transformations.
Morphisms in Algebraic and Projective Varieties
Morphisms between algebraic varieties are regular maps defined by polynomial functions that preserve the algebraic structure, ensuring compatibility with the Zariski topology. In projective varieties, morphisms must respect the projective equivalence, typically given by homogeneous polynomials, making them well-defined on projective coordinate charts. The key difference lies in projective varieties requiring morphisms to be compatible with the scaling action of the projective space, which imposes additional constraints compared to affine algebraic varieties.
Examples of Algebraic and Projective Varieties
Algebraic varieties include examples such as the affine plane curve defined by \( y^2 = x^3 - x \), illustrating solutions within the affine space \( \mathbb{A}^2 \). Projective varieties extend this concept by considering solutions in projective space \( \mathbb{P}^n \), exemplified by the projective closure of the curve \( y^2z = x^3 - xz^2 \) in \( \mathbb{P}^2 \). These varieties differ by their ambient spaces, with projective varieties providing a compactification that resolves issues of infinite points in affine varieties.
The Role of Projective Space in Algebraic Geometry
Projective varieties are defined as the zeros of homogeneous polynomials in projective space, enabling the study of algebraic varieties with added geometric compactness and invariance under scaling. Projective space plays a crucial role in algebraic geometry by allowing varieties to be examined at infinity, thus resolving issues related to the behavior of algebraic sets under limits and ensuring completeness properties. The extension from affine varieties to projective varieties enriches the structural understanding of varieties, facilitating the use of tools like divisors, intersection theory, and cohomology in a compact, well-behaved setting.
Compactness and Completeness: Projective Perspective
Projective varieties are compact within the Zariski topology, a property that algebraic varieties generally lack unless they are projective. This compactness corresponds to the completeness of the projective variety, meaning every morphism from a projective variety to another variety is proper. In contrast, affine or general algebraic varieties are typically non-compact and incomplete, making the projective perspective essential for studying compactness and completeness in algebraic geometry.
Applications and Importance in Modern Mathematics
Algebraic varieties serve as fundamental objects in algebraic geometry, providing the foundation for solving polynomial equations and modeling geometric shapes in affine space, crucial for applications in number theory, cryptography, and robotics. Projective varieties extend these concepts into projective space, allowing the study of properties invariant under projection and enabling a deeper understanding of classification problems, intersection theory, and moduli spaces, which are central in modern string theory and complex geometry. Both varieties are instrumental in advancements in computational algebraic geometry, aiding in algorithm development for symbolic computation and optimization in scientific computing.
Algebraic variety Infographic
 libterm.com
libterm.com