Neutral tannakian categories form a foundational framework in modern algebraic geometry and representation theory, characterized by their equivalence to the category of representations of an affine group scheme over a field. These categories generalize the notion of linear representations of groups, encoding deep symmetries and allowing reconstruction of algebraic groups from categorical data. Explore the full article to uncover how your understanding of tannakian categories can enrich insights into algebraic structures.
Table of Comparison
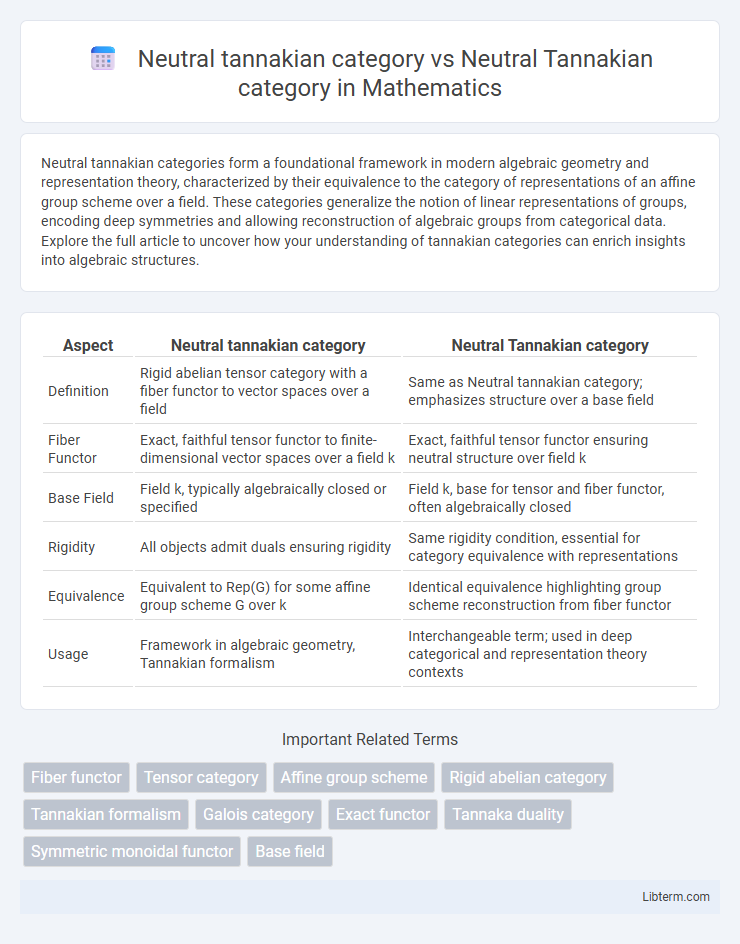
| Aspect | Neutral tannakian category | Neutral Tannakian category |
|---|---|---|
| Definition | Rigid abelian tensor category with a fiber functor to vector spaces over a field | Same as Neutral tannakian category; emphasizes structure over a base field |
| Fiber Functor | Exact, faithful tensor functor to finite-dimensional vector spaces over a field k | Exact, faithful tensor functor ensuring neutral structure over field k |
| Base Field | Field k, typically algebraically closed or specified | Field k, base for tensor and fiber functor, often algebraically closed |
| Rigidity | All objects admit duals ensuring rigidity | Same rigidity condition, essential for category equivalence with representations |
| Equivalence | Equivalent to Rep(G) for some affine group scheme G over k | Identical equivalence highlighting group scheme reconstruction from fiber functor |
| Usage | Framework in algebraic geometry, Tannakian formalism | Interchangeable term; used in deep categorical and representation theory contexts |
Introduction to Neutral Tannakian Categories
Neutral Tannakian categories form a fundamental concept in modern algebraic geometry and representation theory, providing a framework that connects tensor categories with affine group schemes. They are rigid abelian tensor categories equipped with a fiber functor to vector spaces over a fixed field, enabling an equivalence between the category and the representation category of a proalgebraic group. This duality, introduced by Saavedra Rivano and Deligne, allows for the reconstruction of group schemes from tensor categories and plays a crucial role in understanding motives, Galois groups, and fundamental groups in algebraic settings.
Defining Neutral tannakian category (lowercase)
A neutral tannakian category is a rigid abelian tensor category equipped with a faithful exact k-linear fiber functor to the category of finite-dimensional vector spaces over a field k. This structure allows the category to be equivalent to the category of representations of an affine group scheme over k. Defining a neutral tannakian category involves specifying the tensor structure, duals for objects, and compatibility with the fiber functor, ensuring a Tannakian formalism that links category theory and algebraic geometry.
Defining Neutral Tannakian Category (capitalized)
Neutral Tannakian Category refers specifically to a rigid abelian tensor category equipped with a fiber functor to the category of finite-dimensional vector spaces over a field k, allowing a precise Tannakian formalism that connects category theory with group schemes. In contrast, neutral tannakian category (uncapitalized) may denote the general concept without emphasizing the formal structure or the associated fiber functor key to establishing an equivalence with the category of representations of an affine group scheme. The capitalized term highlights the canonical framework essential for reconstructing affine group schemes via tannakian duality, a fundamental tool in modern algebraic geometry and representation theory.
Semantic Differences Between Naming Conventions
The term "Neutral tannakian category" versus "Neutral Tannakian category" primarily differs in capitalization, reflecting the formal naming convention of the mathematical concept. Capitalizing "Tannakian" emphasizes its status as a specialized term in category theory related to tannakian duality and the representation theory of affine group schemes. Using lowercase "tannakian" may imply a more informal or descriptive usage, potentially affecting keyword search optimization and clarity in academic writing.
Formal Usage in Category Theory Literature
The term "Neutral Tannakian category" is capitalized when referring to a specific formal concept in category theory, emphasizing its status as a defined mathematical structure associated with tensor categories possessing a fiber functor to vector spaces over a field. In contrast, "neutral tannakian category" with lowercase letters may appear in informal or expository texts where the precise formal definition is not the focus, thus lacking the standardized notation found in advanced research articles or textbooks. Formal usage in category theory literature consistently prefers the capitalized form to denote the well-established theory connecting Tannakian categories with affine group schemes, ensuring clarity and alignment with established mathematical conventions.
Consistency in Mathematic Notation Standards
Neutral tannakian category and Neutral Tannakian category refer to the same concept in mathematics, specifically within category theory and algebraic geometry, where the term denotes a rigid abelian tensor category with a fiber functor to vector spaces over a field. Consistency in mathematic notation standards emphasizes capitalizing "Tannakian" to align with proper nouns derived from mathematicians' names, ensuring clarity and formal recognition. Adhering to this convention improves readability and maintains uniformity across academic literature in the study of tannakian categories.
Case Sensitivity in Mathematical Terminology
The distinction between "Neutral tannakian category" and "Neutral Tannakian category" highlights the importance of case sensitivity in mathematical terminology, where capitalization often denotes formal definitions or specific concepts. In advanced algebraic geometry and category theory, "Neutral Tannakian category" with capital letters refers to a well-defined structure that admits a fiber functor to the category of vector spaces, while the lowercase variant may imply a general notion or informal reference. Precise usage of case ensures clarity and consistency in mathematical communication, especially in research papers and formal texts.
Impact on Searchability and Indexing
Neutral tannakian category" lowercase usage may reduce search precision as it blends with generic terms, while "Neutral Tannakian category" capitalized aligns with recognized terminology in algebraic geometry and category theory, enhancing visibility in academic databases. Capitalization acts as a semantic marker that improves indexing algorithms' ability to identify it as a specific mathematical concept, increasing relevance in queries related to Tannakian categories. Accurate capitalization supports authoritative indexing, facilitating easier discovery by researchers and improving the semantic clarity of digital repositories.
Recommendations for Academic Writing
In academic writing, the term "Neutral Tannakian category" should be capitalized to reflect its status as a specific, well-defined mathematical concept, enhancing clarity and consistency in scholarly communication. Using "Neutral tannakian category" with lowercase letters may cause ambiguity or diminish the term's significance in the context of tensor categories and Tannakian duality. Maintaining standard capitalization aligns with conventions in category theory literature, ensuring precise and professional presentation of the concept.
Conclusion: Neutral tannakian category vs Neutral Tannakian category
Neutral tannakian category and Neutral Tannakian category refer to the same concept within category theory, with the difference lying solely in capitalization convention. Both describe rigid abelian tensor categories equipped with a fiber functor to vector spaces over a field, enabling the reconstruction of affine group schemes. The emphasis should be on consistent notation rather than conceptual distinction when discussing these categories.
Neutral tannakian category Infographic
 libterm.com
libterm.com