A manifold is a mathematical space that locally resembles Euclidean space and allows for the rigorous study of geometric and topological properties. Its applications span physics, engineering, and computer science, making it essential for understanding complex shapes and higher-dimensional data. Explore this article to deepen your knowledge of manifolds and their practical significance in your field.
Table of Comparison
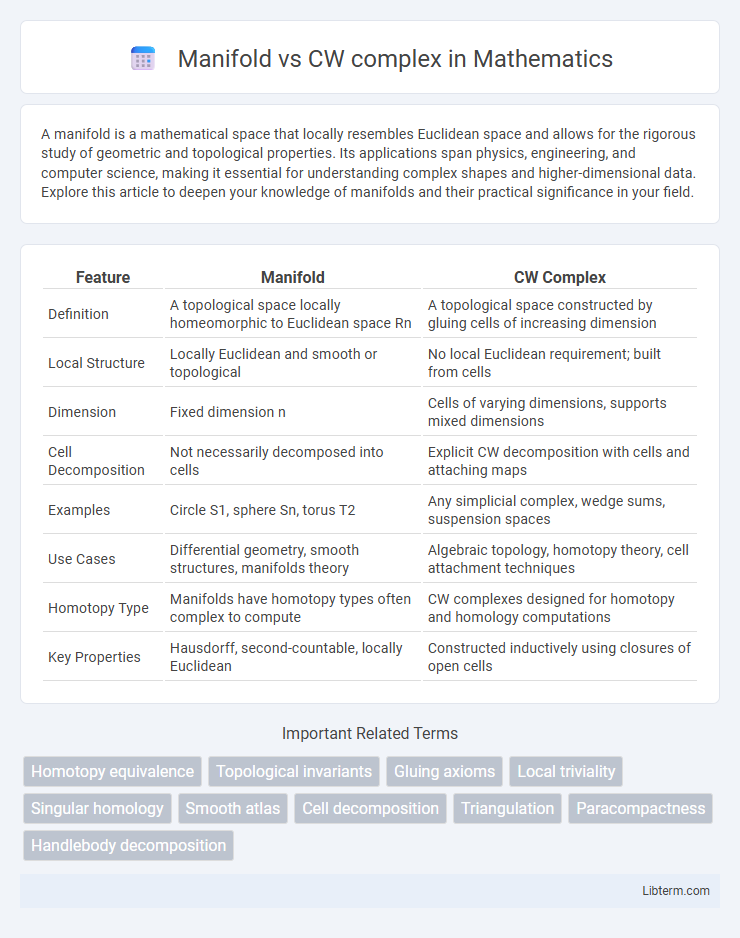
| Feature | Manifold | CW Complex |
|---|---|---|
| Definition | A topological space locally homeomorphic to Euclidean space Rn | A topological space constructed by gluing cells of increasing dimension |
| Local Structure | Locally Euclidean and smooth or topological | No local Euclidean requirement; built from cells |
| Dimension | Fixed dimension n | Cells of varying dimensions, supports mixed dimensions |
| Cell Decomposition | Not necessarily decomposed into cells | Explicit CW decomposition with cells and attaching maps |
| Examples | Circle S1, sphere Sn, torus T2 | Any simplicial complex, wedge sums, suspension spaces |
| Use Cases | Differential geometry, smooth structures, manifolds theory | Algebraic topology, homotopy theory, cell attachment techniques |
| Homotopy Type | Manifolds have homotopy types often complex to compute | CW complexes designed for homotopy and homology computations |
| Key Properties | Hausdorff, second-countable, locally Euclidean | Constructed inductively using closures of open cells |
Introduction to Manifolds and CW Complexes
Manifolds are topological spaces that locally resemble Euclidean space and support calculus through smooth structures, making them central in differential geometry and physics. CW complexes provide a combinatorial framework built from cells of various dimensions, enabling the study of topological spaces via homotopy and homology theory. Understanding the differences between manifolds and CW complexes illuminates their distinct roles in topology: manifolds emphasize local Euclidean structure and smoothness, while CW complexes focus on cellular construction and algebraic invariants.
Fundamental Definitions
A manifold is a topological space that locally resembles Euclidean space and is characterized by its smooth or differentiable structure, enabling calculus and geometric analysis. A CW complex is a type of topological space constructed by gluing cells of varying dimensions, called n-cells, in a combinatorial fashion, facilitating algebraic topology studies such as homology and homotopy. Unlike manifolds, which require local Euclidean properties, CW complexes emphasize cell attachment and can represent more general topological spaces without smoothness constraints.
Topological Foundations
Manifolds and CW complexes serve as fundamental structures in topology, with manifolds characterized by local Euclidean properties enabling smooth calculus, whereas CW complexes build spaces from cells of varying dimensions via attaching maps. The topological foundation of manifolds relies on charts and atlases ensuring local homeomorphisms to Euclidean space, supporting differential structures, while CW complexes emphasize inductive cell attachments to capture homotopy types and flexible decompositions. CW complexes provide a combinatorial framework suitable for homotopy and cohomology theories, contrasting with manifolds' smooth and geometric focus rooted in local Euclidean behavior.
Structure and Construction
Manifolds are topological spaces that locally resemble Euclidean space and are constructed using coordinate charts and smooth transition maps, emphasizing differentiable structure. CW complexes are built inductively by attaching cells of increasing dimension via continuous maps, providing a combinatorial framework ideal for homotopy theory and topological invariants. The key structural difference lies in manifolds' smooth local Euclidean properties versus CW complexes' cell-by-cell assembly, enabling distinct approaches to classification and analysis in topology.
Differentiable Properties
Manifolds possess differentiable structures allowing smooth maps and calculus operations locally modeled on Euclidean spaces, enabling tangent spaces and differentiable charts. CW complexes, built from cells attached via continuous maps, lack inherent differentiable structures and do not generally support smooth transitions or tangent space notions. The differentiability of manifolds facilitates advanced geometric analysis, whereas CW complexes primarily serve topological classification without differentiable constraints.
Homotopy and Homology Perspectives
Manifolds and CW complexes provide distinct frameworks for analyzing homotopy and homology properties, with manifolds being smooth or topological spaces that locally resemble Euclidean space, allowing the application of differential topology tools. CW complexes, built from cells of varying dimensions, offer combinatorial structures that facilitate explicit computation of homotopy groups and cellular homology, often simplifying tasks such as calculating Betti numbers and torsion coefficients. From a homotopy perspective, CW complexes excel in constructing explicit models for spaces up to homotopy equivalence, while manifolds contribute geometric intuition and smooth structure critical for advanced invariants like characteristic classes in homology.
Key Similarities and Differences
Manifolds and CW complexes both serve as foundational structures in topology, allowing the study of shapes and spaces through local and global properties. Manifolds are locally Euclidean, smooth or topological spaces resembling Euclidean space near each point, while CW complexes are built inductively by attaching cells of increasing dimension, emphasizing combinatorial and homotopical methods. Key differences lie in their construction and application: manifolds prioritize smoothness and local geometry, essential in differential geometry and physics, whereas CW complexes prioritize algebraic topology and homotopy theory through a cell-based, discrete framework.
Applications in Mathematics and Physics
Manifolds provide a smooth structure that is essential for differential geometry and general relativity, enabling the formulation of concepts such as curvature, metrics, and geodesics. CW complexes offer a combinatorial framework critical for algebraic topology, used in homotopy theory and the classification of topological spaces through cellular decompositions. In mathematical physics, manifolds model spacetime and fields, while CW complexes facilitate the study of topological quantum field theories and discrete approximations of space.
Examples and Illustrations
A 2-dimensional manifold such as the surface of a sphere is locally homeomorphic to Euclidean space, while a CW complex like the torus built from attaching cells showcases a combinatorial structure enabling homology computations. The Klein bottle exemplifies a non-orientable manifold lacking an embedding in three-dimensional Euclidean space, whereas a CW complex formed by gluing cells can represent the same topological type with explicit cell decomposition. Simplicial complexes and CW complexes provide constructive methods to approximate manifolds through finite cell attachments, facilitating visualization and algebraic topology techniques.
Conclusion and Future Directions
Manifolds provide a locally Euclidean structure enabling smooth calculus applications, whereas CW complexes offer flexible combinatorial decompositions suited for homotopy theory and algebraic topology. The interplay between these frameworks fosters advancements in topological data analysis, geometric group theory, and higher-categorical structures. Future research may explore refining manifold invariants via CW complex techniques and developing computational algorithms to bridge smooth and combinatorial topologies.
Manifold Infographic
 libterm.com
libterm.com