Split resolution divides a display's total pixel count into multiple sections, enhancing image clarity and multitasking capabilities on various screens. This technique optimizes visual performance by allocating specific pixel areas for different content, improving user interaction and experience. Discover how split resolution can transform your display setup by reading the rest of this article.
Table of Comparison
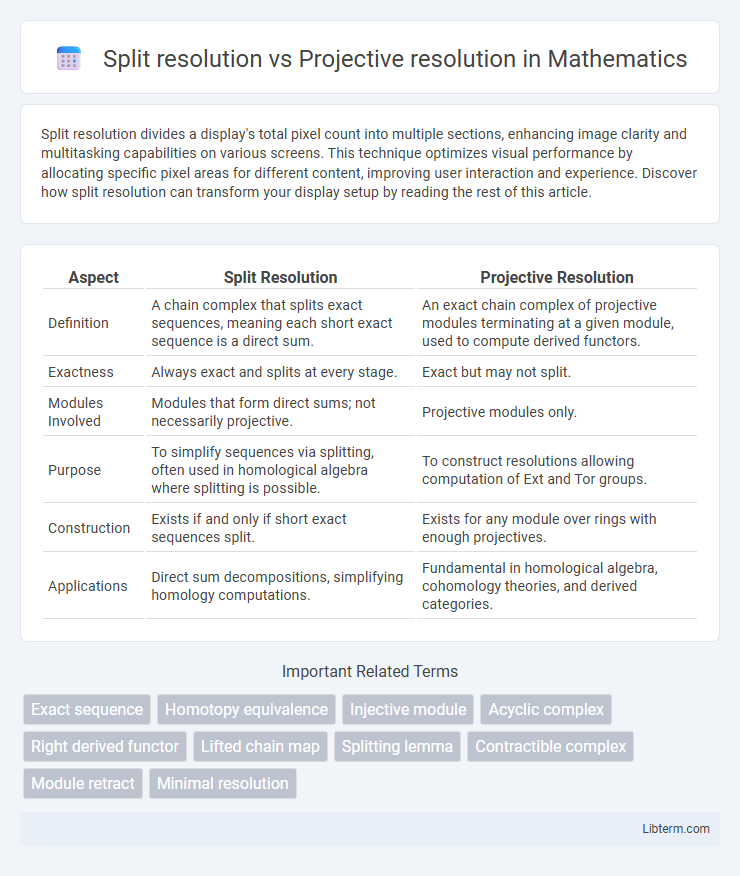
| Aspect | Split Resolution | Projective Resolution |
|---|---|---|
| Definition | A chain complex that splits exact sequences, meaning each short exact sequence is a direct sum. | An exact chain complex of projective modules terminating at a given module, used to compute derived functors. |
| Exactness | Always exact and splits at every stage. | Exact but may not split. |
| Modules Involved | Modules that form direct sums; not necessarily projective. | Projective modules only. |
| Purpose | To simplify sequences via splitting, often used in homological algebra where splitting is possible. | To construct resolutions allowing computation of Ext and Tor groups. |
| Construction | Exists if and only if short exact sequences split. | Exists for any module over rings with enough projectives. |
| Applications | Direct sum decompositions, simplifying homology computations. | Fundamental in homological algebra, cohomology theories, and derived categories. |
Introduction to Resolutions in Homological Algebra
Split resolutions in homological algebra are exact sequences where each short exact sequence splits, allowing the chain complex to be decomposed into simpler components and facilitating explicit computations. Projective resolutions involve exact sequences of projective modules resolving a given module, crucial for defining derived functors like Tor and Ext in homological contexts. These resolutions serve as foundational tools for understanding module structure and computing homological invariants in algebraic topology and algebraic geometry.
Defining Split Resolution
A split resolution is a projective resolution in which each short exact sequence in the chain complex splits, allowing every module to be a direct summand of the next. This splitting condition ensures that the resolution is not only exact but also decomposes into simpler components, facilitating explicit computations in homological algebra. Projective resolutions, by contrast, need only satisfy exactness without requiring the sequences to split, making split resolutions a stronger and more structured notion.
Understanding Projective Resolution
Projective resolutions provide a structured way to analyze modules by expressing them as exact sequences of projective modules, enabling deep insights into homological dimensions and derived functors. Unlike split resolutions, which require exact sequences to split, projective resolutions do not necessitate direct summand conditions, allowing broader applicability in module theory. Understanding projective resolutions is crucial for computing Ext and Tor groups, fundamental tools in homological algebra and category theory.
Key Differences Between Split and Projective Resolutions
Split resolutions feature exact sequences that split, ensuring each module in the sequence is a direct summand, which simplifies their structure and guarantees the existence of a right inverse morphism. Projective resolutions consist of exact sequences where each module is projective, enabling the construction of free-like modules that provide a powerful tool in homological algebra for computing derived functors. The key difference lies in the splitting condition; split resolutions are always projective but impose a stricter splitting condition, while projective resolutions do not require sequences to split but rely on the projectivity of modules to resolve complex algebraic objects.
Criteria for a Resolution to be Split
A split resolution requires the existence of a chain map that acts as a right inverse to the inclusion maps, ensuring each short exact sequence in the resolution splits. This condition guarantees the resolution decomposes into a direct sum of complexes, reflecting projective modules with retraction maps at every stage. Consequently, verifying split criteria involves identifying homotopy equivalences or splitting homomorphisms that preserve module structures and enable explicit decomposition.
Examples of Split Resolutions
Split resolutions occur when a short exact sequence of modules 0 - A - B - C - 0 splits, meaning B is isomorphic to the direct sum A C, allowing straightforward construction of projective resolutions. For example, if A and C are projective modules, the sequence splits and the resolution can be explicitly described by combining their projective resolutions. Another instance is the splitting of the sequence 0 - Z - Z Z - Z - 0, where the middle term is a direct sum, simplifying the resolution and eliminating extension complexities.
Applications of Projective Resolutions
Projective resolutions are fundamental in homological algebra and algebraic topology for computing derived functors such as Ext and Tor, which reveal extensions and relations between modules. They facilitate the classification of modules via homological dimensions and assist in resolving complex modules into simpler projective components, enabling effective computations in category theory and representation theory. Unlike split resolutions, projective resolutions provide essential tools for analyzing non-split exact sequences and studying the structural properties of modules over rings.
When Split and Projective Resolutions Coincide
Split resolutions coincide with projective resolutions when every exact sequence in the resolution splits, meaning each short exact sequence decomposes into a direct sum. This occurs if and only if all modules in the resolution are not only projective but also possess additional splitting properties, such as being retracts of free modules. In categories like modules over semisimple rings, all projective resolutions are split, ensuring an equivalence between split and projective resolutions.
Advantages and Limitations of Each Resolution
Split resolutions provide explicit splitting maps that simplify computations in homological algebra, making it easier to analyze modules with projective decompositions, but they are limited to modules that admit such splittings, restricting their applicability. Projective resolutions offer a more general framework applicable to any module, facilitating the calculation of derived functors like Ext and Tor, although their construction can be complex and less explicit, often involving infinite or non-split exact sequences. While split resolutions enhance clarity and computational ease for split modules, projective resolutions ensure broader utility but require more nuanced handling in homological computations.
Summary and Practical Implications
Split resolutions guarantee exact sequence decompositions with explicit splitting maps, simplifying the computation of homological invariants by providing canonical retracts. Projective resolutions, while potentially more complex, offer broader applicability in deriving functor cohomology and Ext groups, essential for classifying module structures and extensions. The choice between split and projective resolutions impacts the ease of calculations and the generality of homological results in algebraic topology and homological algebra.
Split resolution Infographic
 libterm.com
libterm.com