Calabi-Yau manifolds are complex, multidimensional shapes pivotal in string theory and algebraic geometry, providing the mathematical structure for compactifying extra dimensions in the universe. Their unique properties, such as Ricci-flatness and complex geometry, enable profound insights into the nature of space-time and particle physics. Explore the rest of the article to understand how Calabi-Yau manifolds impact modern theoretical physics and mathematics.
Table of Comparison
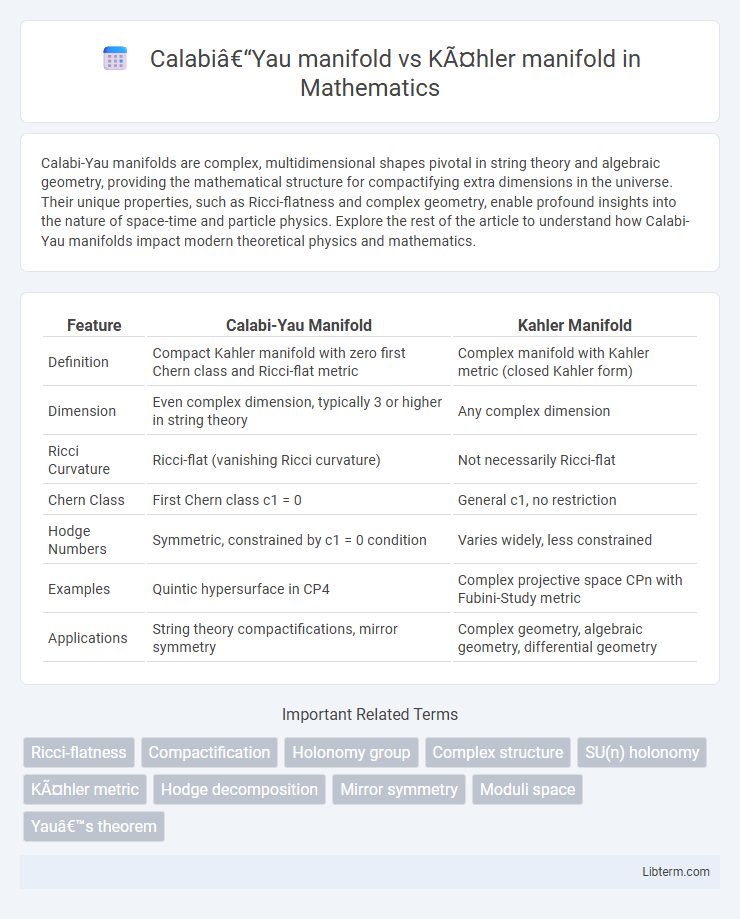
| Feature | Calabi-Yau Manifold | Kahler Manifold |
|---|---|---|
| Definition | Compact Kahler manifold with zero first Chern class and Ricci-flat metric | Complex manifold with Kahler metric (closed Kahler form) |
| Dimension | Even complex dimension, typically 3 or higher in string theory | Any complex dimension |
| Ricci Curvature | Ricci-flat (vanishing Ricci curvature) | Not necessarily Ricci-flat |
| Chern Class | First Chern class c1 = 0 | General c1, no restriction |
| Hodge Numbers | Symmetric, constrained by c1 = 0 condition | Varies widely, less constrained |
| Examples | Quintic hypersurface in CP4 | Complex projective space CPn with Fubini-Study metric |
| Applications | String theory compactifications, mirror symmetry | Complex geometry, algebraic geometry, differential geometry |
Introduction to Complex Manifolds
Calabi-Yau manifolds are a special class of Kahler manifolds characterized by vanishing first Chern class and Ricci-flat metrics, playing a crucial role in string theory and complex geometry. Kahler manifolds provide a rich structure combining symplectic, complex, and Riemannian geometry, essential for studying complex manifolds. Understanding the relationship between these manifolds illuminates fundamental aspects of complex geometry and theoretical physics.
Defining Kähler Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated two-form is closed, making them simultaneously complex, symplectic, and Riemannian manifolds. The defining feature is the existence of a Kahler form, a closed, non-degenerate (1,1)-form that satisfies do = 0, ensuring compatibility between the metric, complex structure, and symplectic structure. Calabi-Yau manifolds are special cases of Kahler manifolds characterized by Ricci-flat Kahler metrics and vanishing first Chern class, important in string theory and complex geometry.
Understanding Calabi–Yau Manifolds
Calabi-Yau manifolds are a special subset of Kahler manifolds characterized by a vanishing first Chern class, allowing for Ricci-flat metrics important in string theory compactifications. These complex manifolds have SU(n) holonomy, which preserves supersymmetry in theoretical physics models. Understanding their geometric structure provides key insights into mirror symmetry and moduli spaces in algebraic geometry.
Core Properties of Kähler Manifolds
Kahler manifolds possess a Hermitian metric compatible with a symplectic structure, characterized by a closed Kahler form that integrates complex, symplectic, and Riemannian geometry. These manifolds exhibit rich topological properties, such as Hodge decomposition and the -lemma, which enable powerful techniques in complex geometry. Calabi-Yau manifolds represent a special subclass of Kahler manifolds distinguished by Ricci-flat metrics and vanishing first Chern class, playing a critical role in string theory compactifications.
Characteristic Features of Calabi–Yau Manifolds
Calabi-Yau manifolds are complex Kahler manifolds distinguished by having a vanishing first Chern class and admitting a Ricci-flat Kahler metric, which is essential for supersymmetry in string theory compactifications. These manifolds possess a holomorphically trivial canonical bundle, enabling the existence of a nowhere vanishing holomorphic volume form, a key feature absent in general Kahler manifolds. The unique combination of Ricci-flatness and complex structure conditions sets Calabi-Yau manifolds apart by providing the geometric framework for mirror symmetry and moduli space analysis in mathematical physics.
Calabi–Yau Manifolds as Special Kähler Manifolds
Calabi-Yau manifolds are a specific subset of Kahler manifolds characterized by their vanishing first Chern class and Ricci-flat metric, making them essential in string theory and complex geometry. These special Kahler manifolds possess a holonomy group contained in SU(n), which distinguishes them from general Kahler manifolds with U(n) holonomy. Their intricate geometric structure supports supersymmetry and compactification scenarios in theoretical physics.
Key Mathematical Differences
Calabi-Yau manifolds are a special class of Kahler manifolds characterized by having a Ricci-flat metric and a trivial canonical bundle, which implies zero first Chern class. Kahler manifolds possess a Hermitian metric whose imaginary part is a closed 2-form, but they do not necessarily have Ricci-flat metrics or trivial canonical bundles. The defining condition that distinguishes Calabi-Yau manifolds is the existence of a nowhere vanishing holomorphic volume form, enabling the manifold to satisfy the Calabi conjecture and yield a Ricci-flat geometry.
Physical Relevance in String Theory
Calabi-Yau manifolds play a crucial role in string theory as compactification spaces that preserve supersymmetry, crucial for obtaining realistic four-dimensional physics from ten-dimensional superstring theory. Kahler manifolds provide the broader geometric framework with a compatible complex structure and symplectic form, but only Calabi-Yau manifolds have vanishing first Chern class, enabling Ricci-flat metrics essential for anomaly cancellation and stable vacuum solutions. The physical relevance of Calabi-Yau manifolds arises from their ability to yield chiral matter and gauge groups consistent with particle physics, whereas generic Kahler manifolds lack these stringent properties.
Examples and Applications
Calabi-Yau manifolds, a special class of Kahler manifolds with vanishing first Chern class, are pivotal in string theory for compactifying extra dimensions while preserving supersymmetry. Classic examples include the quintic threefold, which serves as a foundational model in mirror symmetry and complex geometry. Kahler manifolds, more broadly, appear in algebraic geometry and theoretical physics, with applications ranging from Hodge theory to complex differential geometry, exemplified by complex projective spaces and toric varieties.
Summary: Calabi–Yau vs Kähler Manifold
Calabi-Yau manifolds are a special class of Kahler manifolds characterized by Ricci-flat metrics and vanishing first Chern class, making them crucial in string theory and complex geometry. Kahler manifolds possess a Hermitian metric with a closed Kahler form, allowing compatible complex, symplectic, and Riemannian structures without the Ricci-flat condition. The key difference lies in Calabi-Yau manifolds satisfying additional geometric constraints, which enable unique properties such as mirror symmetry and moduli space stability.
Calabi–Yau manifold Infographic
 libterm.com
libterm.com