A Borel set is a fundamental concept in measure theory and topology, defined as any set that can be formed from open or closed sets through countable unions, intersections, and complements. These sets form the Borel sigma-algebra, crucial for defining measures like the Lebesgue measure and analyzing measurable functions. Explore the rest of the article to understand how Borel sets underpin modern probability and real analysis.
Table of Comparison
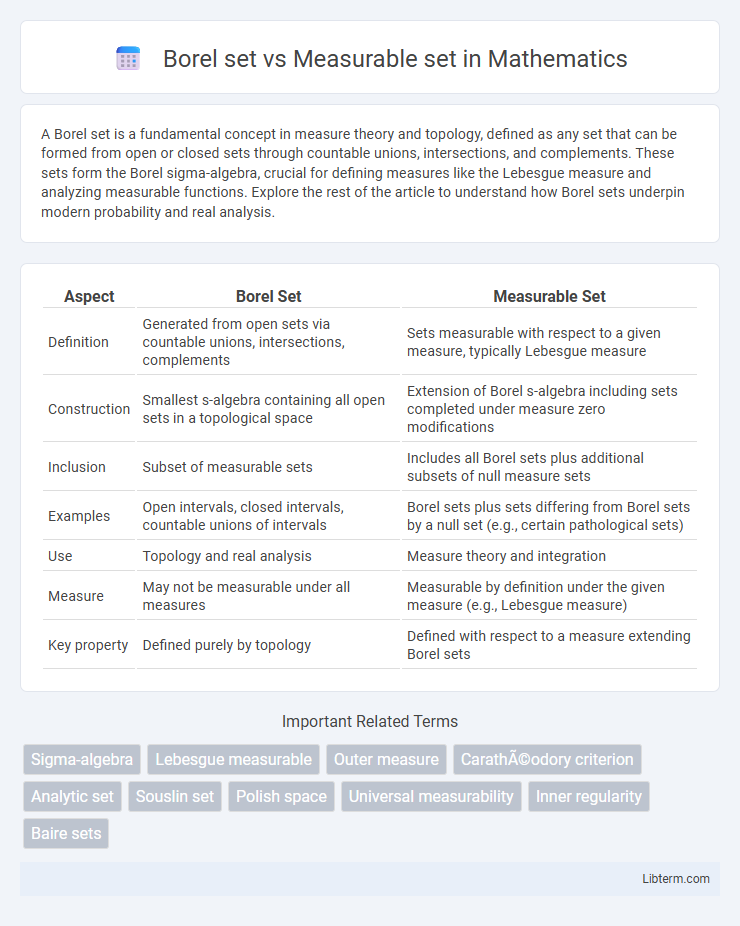
| Aspect | Borel Set | Measurable Set |
|---|---|---|
| Definition | Generated from open sets via countable unions, intersections, complements | Sets measurable with respect to a given measure, typically Lebesgue measure |
| Construction | Smallest s-algebra containing all open sets in a topological space | Extension of Borel s-algebra including sets completed under measure zero modifications |
| Inclusion | Subset of measurable sets | Includes all Borel sets plus additional subsets of null measure sets |
| Examples | Open intervals, closed intervals, countable unions of intervals | Borel sets plus sets differing from Borel sets by a null set (e.g., certain pathological sets) |
| Use | Topology and real analysis | Measure theory and integration |
| Measure | May not be measurable under all measures | Measurable by definition under the given measure (e.g., Lebesgue measure) |
| Key property | Defined purely by topology | Defined with respect to a measure extending Borel sets |
Introduction to Borel Sets and Measurable Sets
Borel sets are defined as the smallest s-algebra containing all open sets in a given topological space, fundamental in topology and measure theory. Measurable sets extend this concept by belonging to a s-algebra equipped with a measure, allowing the assignment of a consistent size or probability. Understanding the distinction between Borel sets and measurable sets is crucial for analyzing which sets can be effectively measured in spaces with complex structures.
Foundations: Topological vs. Measure Theory Perspectives
Borel sets arise from the smallest s-algebra containing all open sets in a topological space, reflecting a foundational concept in topology through the construction of measurable structures via open set operations. Measurable sets extend beyond Borel sets by incorporating the completion of a measure, such as the Lebesgue measure, ensuring all null sets and their subsets are included within the measure-theoretic framework. This distinction highlights the topological origins of Borel sets versus the measure-theoretic enrichment that defines measurable sets, critical for integrating abstract topology with practical measure applications.
Defining Borel Sets: Generation from Open Sets
Borel sets are generated from open sets through the smallest s-algebra containing all open subsets of a topological space, making them fundamental in measure theory and topology. Measurable sets extend beyond Borel sets by including those sets measurable with respect to a given measure, such as the Lebesgue measure, capturing more complex sets like subsets of null sets. The Borel s-algebra is thus a canonical starting point, formed via countable unions, intersections, and complements of open sets, whereas measurable sets encompass this and additional sets defined via completion of the measure.
Construction of Measurable Sets: Sigma-Algebras and Measures
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest s-algebra on a topological space. Measurable sets extend this concept by belonging to a s-algebra equipped with a measure, such as Lebesgue measure, allowing integration and probability frameworks. The construction of measurable sets involves completing the Borel s-algebra to include subsets of null sets, ensuring closure under measure-theoretic limits and facilitating robust analysis in measure theory.
Relationships and Differences: Borel vs. Measurable Sets
Borel sets form the smallest s-algebra generated by open sets in a topological space, serving as a fundamental class of sets in measure theory. Measurable sets include all Borel sets and extend to those sets measurable with respect to a given measure, often incorporating sets that are not Borel but still measurable under completion of the measure. The key difference lies in the fact that every Borel set is measurable, but not every measurable set is Borel, highlighting the broader scope of measurable sets in capturing measure-theoretic properties beyond topological construction.
Examples Illustrating Borel and Non-Borel Measurable Sets
Borel sets consist of all sets that can be formed from open or closed sets through countable unions, intersections, and complements, such as intervals like [0,1] or countable unions of disjoint intervals. A classic example of a Borel set is the Cantor set, constructed using countable operations starting from closed intervals. Non-Borel measurable sets often arise from more complex constructions using the axiom of choice, like Vitali sets, which are measurable but do not belong to the Borel s-algebra.
Significance in Real Analysis and Probability
Borel sets, generated from open intervals through countable unions and intersections, form the foundational sigma-algebra in real analysis, essential for defining Borel measures and enabling rigorous integration theory. Measurable sets extend beyond Borel sets by including sets measurable with respect to a given measure, like the Lebesgue measure, allowing for a more comprehensive treatment of functions and convergence theorems in probability theory. This distinction is crucial in probability, where measurable sets ensure the well-definedness of probabilistic events and the applicability of advanced results like the Law of Large Numbers and Central Limit Theorem.
Applications in Integration and Function Spaces
Borel sets, generated from open sets through countable unions and intersections, form the foundational s-algebra used in defining Borel measures, essential for integration in classical analysis. Measurable sets, which may extend beyond Borel sets to include those completed under a given measure, enable integration of a broader class of functions, crucial in Lebesgue integration and advanced function spaces like L^p spaces. The distinction impacts the ability to approximate integrable functions, influencing convergence theorems and the representation of functions in spaces used for solving differential equations and harmonic analysis.
Common Misconceptions and Clarifications
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the Borel sigma-algebra, while measurable sets extend this concept by including all subsets measurable with respect to a given measure, such as the Lebesgue measure. A common misconception is that all measurable sets are Borel sets; however, measurable sets form a strictly larger class, encompassing sets that are not Borel but still measurable. Clarifying this distinction is crucial in measure theory, as it underpins the difference between topological structure (Borel sets) and measure-theoretic completeness (measurable sets).
Conclusion: Choosing Between Borel and Measurable Sets
Choosing between Borel sets and measurable sets depends on the context of measure theory and probability applications, where measurable sets provide a broader framework that includes all Borel sets plus additional sets necessary for completeness. Borel sets are generated from open sets through countable operations, making them useful for standard topological spaces, but measurable sets extend this concept to ensure every subset of a null set is also measurable, crucial for defining complete measures like the Lebesgue measure. In practical terms, measurable sets offer more flexibility and robustness, especially when dealing with complex or irregular sets beyond the scope of Borel algebra.
Borel set Infographic
 libterm.com
libterm.com